20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) xác định, liên tục và có bảng biến thiên
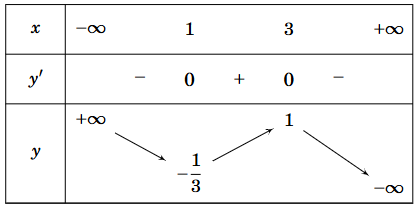
Khẳng định nào sau đây là đúng?
Hàm số có hai điểm cực trị.
Hàm số có giá trị lớn nhất bằng 1 và có giá trị nhỏ nhất bằng 
.
Đồ thị hàm số không cắt trục hoành.
Hàm số có giá trị cực đại bằng 3.
Cho hàm số y = f(x) có bảng biến thiên như sau
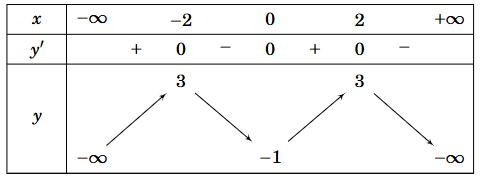
Xét ba khẳng định sau:
1) Hàm số đồng biến trên khoảng (0; 2).
2) Hàm số có một cực đại.
3) Hàm số có giá trị lớn nhất bằng 3.
Số khẳng định đúng trong ba khẳng định trên là
1.
2.
3.
0.
Cho hàm số có bảng biến thiên như hình vẽ. Tìm giá trị nhỏ nhất của hàm số trên đoạn [−2; 3].
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số f(x) liên tục trên đoạn [−2; 3] và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên [−2; 3]. Giá trị M – m bằng
5.
1.
4.
2.
Cho hàm số y = f(x) có đồ thị như sau
Giá trị nhỏ nhất của hàm số đã cho trên đoạn [−2; 0] là
−1.
−4.
−2.
1.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn [−1; 1].
M + m = 2.
M + m = −2.
M + m = 0.
M + m = −3.
Tìm giá trị nhỏ nhất N của hàm số y = x3 – 3x2 + 3x + 2 trên đoạn [−1; 2].
N = 3.
N = 2.
N = 4.
N = −5.
Gọi m, M lần lượt là giá trị nhỏ nhất và lớn nhất của hàm số 
. Khi đó M – m bằng
4.
B. 
.
C. 
.
D. 
.
Giá trị nhỏ nhất của hàm số 
trên khoảng (0; +∞) là
2.
3.
4.
5.
Cho hàm số y = cos2x – 2sinx + 1 với 
. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Khi đó tổng M + m bằng bao nhiêu?
1.
2.
−2.
1.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
a) 
.
b) M = f(5).
c) m = f(−1).
d) M + m = 5.
a) m = −4.
b) M = −1.
c) M + m = −4.
d) Hàm số đạt giá trị lớn nhất tại x = −1
a) 
.
b) 
.
c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên [−1; 1] là 7.
d) 
.
a) Nếu cơ sở bán mỗi chiếc khăn với giá 37000 đồng thì số tiền lãi sau 1 tháng là 44 triệu đồng.
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm x nghìn đồng thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức f(x) = −100x2 + 1800x + 36000.
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm 800 chiếc
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá 39000 đồng.
a) Chiều cao hộp sữa là 
cm.
b) Diện tích toàn phần của hộp sữa là 
(cm2).
c) x = 10 là nghiệm của phương trình y' = 0
d) Diện tích toàn phần nhỏ nhất của hộp sữa là 600 cm3
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 
trên đoạn [0; 3]. Tổng S = 2M – m bằng bao nhiêu?
Cho hàm số y = f(x) có đồ thị như hình vẽ
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
trên đoạn [0; 2]. Tính M + m.
Một vật bắt đầu chuyển động theo quy luật s = −2t3 + 24t2 + 9t – 3 với t là khoảng thời gian tính từ lúc bắt đầu chuyển động và s là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu m/s?
Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 nghìn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 nghìn đồng thì có thêm 2 phòng trống. Giám đốc phải chọn giá phòng mới là bao nhêu để thu nhập của khách sạn trong ngày là lớn nhất (đơn vị nghìn đồng)?
Người ta muốn xây một cái bể hình hộp chữ nhật có thể tích V = 18 m3, biết đáy bể là hình chữ nhật có chiều dài gấp 3 lần chiều rộng và bể không có nắp. Giá thuê nhân công để xây bể là 500000 đồng/m2. Hỏi cần xây bể có chiều cao bằng bao nhiêu mét để chi phí thuê nhân công là thấp nhất.
