Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 3
22 câu hỏi
PHÀN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(f(x)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị như hình vẽ bên dưới. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên \(\left[ { - 1;5} \right]\). Giá trị của \(M - m\) bằng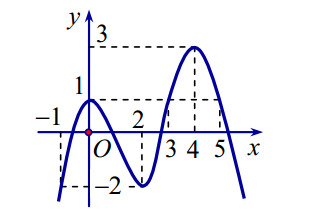
\(1\).
\(6\).
\(5\).
\(4\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 4;5} \right]\), có bảng biến thiên![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 4;5} \right]\), có bảng biến thiên G (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/7-1759147293.png)
Gọi \(M,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) xác định trên đoạn \(\left[ { - 4;5} \right]\). Tính \(M + N\)?
\( - \frac{{16}}{3}\).
\[ - \frac{{50}}{3}\].
2.
\( - 20\).
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{x - 2}}{{x + 1}}\) trên đoạn \(\left[ {0;2} \right]\)
\(2.\).
\( - 3\).
\( - 2.\).
\(0.\)
Tìm giá trị lớn nhất của hàm số \[y = f(x) = \frac{x}{{{x^2} + 1}}\] trên nửa khoảng \(\left( {0; + \infty } \right)\)
\[2\].
\[\frac{1}{2}\].
\[\frac{1}{4}\].
\[4\].
Cho hàm số \(y = 3\sin 2025x + 5\). Tìm giá trị lớn nhất của hàm số
\(6080\).
\(8\).
\(5\).
\(2\).
Cho hàm số \(y = \frac{{x - 3}}{{2x - 5}}\). Tìm tổng giá trị nhỏ nhất và lớn nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\)?
\[\frac{{11}}{7}\].
\(\frac{{13}}{5}.\)
\[\frac{8}{5}.\]
\(\frac{{14}}{9}\).
Cho hàm số \(y = {x^3} + 3{x^2} - 45x - 3\). Tìm tích giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn \[\left[ { - 2;4} \right]\].
\[ - 6305.\]
\( - 7566\).
\( - 7546\).
\( - 7656\).
Cho hàm số \(y = {e^{2x}} - 5{e^x} + 2x\). Tìm giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;2} \right]\)?
\({e^2} - 12\).
\( - 4\).
\[2\ln 2 - 6\].
\(\ln 2 - 6\).
Gọi \(m\) và \(M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = x + \sqrt {2 - {x^2}} \). Khi đó \(M - m\) bằng
\(4\).
\(0\).
\(2 + \sqrt 2 \).
\(2 - \sqrt 2 \).
Hàm số \[y = \frac{{x - {m^2}}}{{x + 1}}\] có giá trị nhỏ nhất trên đoạn \[\left[ {0;1} \right]\] bằng \( - 4\) khi
\[\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\].
\[\left[ \begin{array}{l}m = 3\\m = - 3\end{array} \right.\].
\[m = 2\].
\[m = 3\].
Giá trị nhỏ nhất của hàm số \(y = {\rm{co}}{{\rm{s}}^2}2x - 2\sin x \cdot \cos x + 4\) bằng
\(5\).
\(\frac{{21}}{4}\).
\(\frac{{11}}{4}\).
\(3\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f'\left( x \right)\) được cho trong hình vẽ dưới đây.
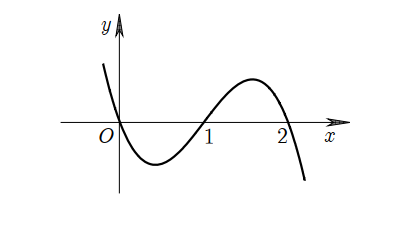
Giá trị nhỏ nhất của hàm số \(g\left( x \right) = f\left( {\sin \,x} \right)\) trên đoạn \(\left[ {0;\pi } \right]\) là
\(f\left( 0 \right)\).
\(f\left( 1 \right)\).
\(f\left( {\frac{{\sqrt 3 }}{2}} \right)\).
\(f\left( {\frac{1}{2}} \right)\).
PHÀN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên:
![Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là \( - 1\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/10-1759147750.png)
a) Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là \( - 1\).
b) Giá trị nhỏ nhất của hàm số trên \(\left[ {0; + \infty } \right)\) là \( - 5\).
c) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên \(\left( { - \infty ;1} \right]\) là 2.
d) Hàm số đạt giá trị nhỏ nhất trên đoạn \(\left[ { - 1;2} \right]\) tại điểm \(x = 1\).
Cho hàm số \(y = f(x) = \frac{{{x^2} + mx + 1}}{{x + m}}\).
a) Khi \(m = 0\), ta có \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 2\).
b) Hàm số đã cho luôn có 2 cực trị.
c) Với mọi giá trị của \(m\), ta luôn có \(\mathop {\min }\limits_{\left( { - m; + \infty } \right)} y - \mathop {{\mathop{\rm m}\nolimits} ax}\limits_{\left( { - \infty ; - m} \right)} y = 4\).
d) Khi \(m = - 3\) thì giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\) bằng \(1\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {1\,;\,3} \right]\].
![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {1\,;\,3} \right]\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759147890.png)
Khẳng định | Đúng | Sai | |
a) | \(m = - 4\). |
|
|
b) | \(M = - 2\) |
|
|
c) | \(M + m = - 4\) |
|
|
d) | Giá trị lớn nhất của hàm số \(y = f\left( x \right) + 4\) trên nửa khoảng \(\left[ { - 1\,;\, + \infty } \right)\) là \(0\). |
|
|
Cho hàm số\[y = f(x) = {x^4} - 2{x^2} - 2\].
Khẳng định | Đúng | Sai | |
a) | Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1\,;\,1} \right]\) là \( - 3\). |
|
|
b) | Giá trị lớn nhất của hàm số trên nửa khoảng \(\left[ { - 1\,;\, + \infty } \right)\) là \( - 2\). |
|
|
c) | Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2\,;\,2} \right]\)là \(3\). |
|
|
d) | Nếu\(\mathop {\min y}\limits_{\left[ {0\,;\,\,2} \right]} = f({x_A}) = {y_A}\), \(\mathop {\max y}\limits_{\left[ {0\,;\,2} \right]} = f({x_B}) = {y_B}\) thì \(AB = \sqrt 2 \) |
|
|
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 9}}{x}\) trên khoảng \((0; + \infty )\).
Tìm giá trị nhỏ nhất của hàm số:\(g(x) = \frac{{\ln x}}{x}\) trên đoạn [1 ; 4].
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G\left( x \right) = 0,035{x^2}\left( {15 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
Một nhóm bạn đi Picnic muốn cắm trại qua đêm. Biết trại cắm là một hình chóp tam giác đỉnh \(S\) cách đều các chân trại \(A,B,C\) một đoạn bằng \(3m\). Biết đáy trại là một tam giác vuông tại \(A\) và \(AB = 2m\). Nhóm muốn cắm trại sao cho thể tích của trại là lớn nhất cho không gian thoải mái. Khi đó độ dài \(AC\) bằng bao nhiêu?
Trong cuộc thi 2 môn phối hợp gồm chèo thuyền và chạy bộ. Các vận động viên sẽ chèo thuyền từ điểm xuất phát \(A\)cách bờ \(BC\)\(6km\) sau đó đến bờ tại một vị trí \(D\) bất kì rồi chạy về đích \(C\),(xem hình minh họa). Biết rằng quãng đường trên bờ \(BC = 15km\), vận tốc chèo thuyền của một vận động viên \(X\)là \(8km/h\) và vận tốc chạy trên bờ là \(16km/h\)
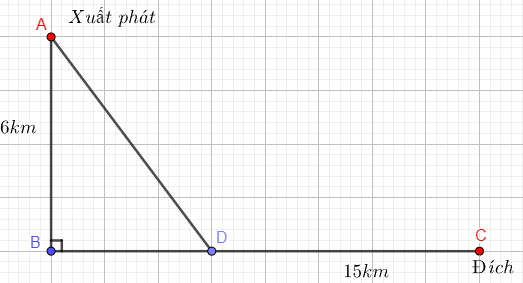
Hỏi \(X\) nên chèo thuyền về bờ tại vị trí \(D\) cách đích \(C\) là bao nhiêu để tổng thời gian về đích là sớm nhất.
Người ta muốn xây một cái bể hình hộp đứng có thể tích \(V = 18\,\,\left( {{m^3}} \right)\), biết đáy bể là hình chữ nhật có chiều dài gấp \(3\) lần chiều rộng và bể không có nắp. Hỏi cần xây bể có chiều cao \(h\) bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất?.