Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 4
22 câu hỏi
PHÀN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \[\left[ { - 1;3} \right]\] và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ { - 1;2} \right]\]bằng 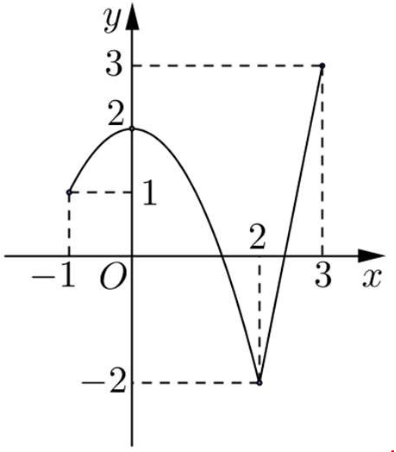
\[3\].
1.
\[ - 2\].
\[2\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) và có bảng biến thiên như hình dưới đây. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 1;2} \right]\). Giá trị của \(M + m\) bằng bao nhiêu ?![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) và có bảng biến thiên như hình dưới đây. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 1;2} \righ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759148646.png)
\(3\).
\(2\).
\(1\).
\(4\).
Gọi \[m\] là giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn \(\left[ {2;4} \right]\). Khi đó:
\(m = 6\).
\(m = - 2\).
\(m = - 3\).
\(m = \frac{{19}}{3}\).
Tìm giá trị nhỏ nhất của hàm số \[y = f\left( x \right) = {x^2} - 3x\] trên đoạn \(\left[ {0;2} \right].\)
\[ - \frac{9}{4}\].
\[ - \frac{3}{2}\].
\[0\].
\[5\].
Cho hàm số \[y = f\left( x \right)\] xác định, liên tục trên đoạn \[\left[ { - 2\,;\,2} \right]\] và có đồ thị là đường cong trong hình vẽ sau: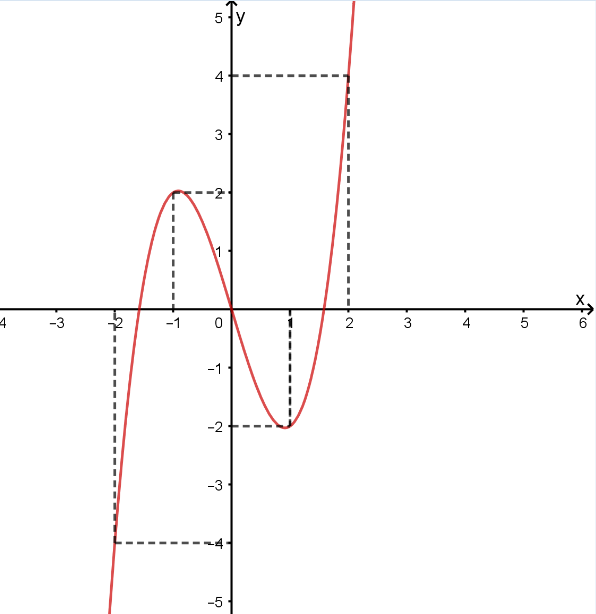
Tìm khẳng định đúng trong các khẳng định sau:
\[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 4\].
\[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 1\].
\[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = 2\].
\[\mathop {\min }\limits_{\left[ { - 2\,;\,2} \right]} f\left( x \right) = - 2\].
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
![Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau: Giá trị lớn nhất của hàm số \(y = f\left( x \right)\)trên đoạn \(\left[ {0;2} \right]\) bằng A. \(1\). B. \(3\). C. \(0\). D. \(2\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1759148815.png)
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\)trên đoạn \(\left[ {0;2} \right]\) bằng
\(1\).
\(3\).
\(0\).
\(2\).
Tìm giá trị lớn nhất của hàm số \[f\left( x \right) = \frac{1}{{40}}{x^2}\left( {30 - x} \right)\] trên nửa khoảng \[\left( {0; + \infty } \right)\]
\[20\].
\[24\].
\[25\].
\[30\].
Cho hàm số \(y = {2^x} - 4x\ln 2\). Giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {0;4} \right]\] có dạng \(a - b\ln c\). Tính \(a + b + c\)?
\( - 2\).
\(14.\)
\(34.\)
\(0\).
Gọi \(m,M\) lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số \(y = x - \ln x\) trên đoạn \(\left[ {\frac{1}{2};e} \right]\). Giá trị của \(M - m\) là:
\(e - \ln 2 - \frac{1}{2}\).
\(e - 1\).
\(\ln 2 - \frac{1}{2}\).
\(e - 2\).
Cho hàm số \(y = f\left( x \right) = \sqrt {4 - {x^2}} .\) Khẳng định nào sau đây là sai?
Hàm số có GTLN là 2.
Hàm số có GTNN là 0.
Hàm số đạt GTLN tại \(x = 2.\)
Hàm số đạt GTNN tại \(x = \pm 2.\)
Cho hàm số \(y = f\left( x \right) = x - 5 + \frac{1}{x}\), xét trên khoảng \(\left( {0;\; + \infty } \right)\)giá trị nhỏ nhất của hàm số bằng
\(0\).
\( - 3\).
\(4\).
\( - 4\).
Để hàm số\(y = - {x^4} + 6{x^2} + m\)đạt giá trị lớn nhất trên \(\left[ { - 1;1} \right]\) bằng 5 thì giá trị của tham số \(m\)bằng
\(0\).
\(5\).
\( - 5\).
\(1\).
PHÀN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f\left( x \right) = 2{x^2} + \frac{{500}}{x}\). Xét tính đúng sai của các mệnh đề sau
a)\(f'\left( x \right) = 0 \Leftrightarrow x = 5\).
b)\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\).
b)Giá trị nhỏ nhất của hàm số trên \[\left( {0;5} \right)\] là 150.
c)Giá trị nhỏ nhất của hàm số trên \[\left( {0; + \infty } \right)\] là 150.
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30.000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\).
a) Nếu cơ sở bán mỗi chiếc khăn với giá \(37000\)(đồng) thì số tiền lãi sau 1 tháng là \(44\)(triệu đồng).
b) Sau khi cơ sở tăng giá mỗi chiếc khăn thêm \(x\) (nghìn đồng) thì tổng số lợi nhuận một tháng của cơ sở được tính theo công thức\(f\left( x \right) = - 100{x^2} + 1800x + 36000\).
c) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc.
d) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng.
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Khẳng định | Đúng | Sai | |||
\(\mathop {\max }\limits_{x \in \mathbb{R}} f\left( x \right) = 5.\) |
|
|
| ||
\(\mathop {\min }\limits_{x \in \mathbb{R}} f\left( x \right) = 2.\) |
|
|
| ||
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên \(\left[ { - 1;1} \right]\)là 7 |
|
|
| ||
\(\mathop {\max }\limits_{x \in \left[ {0;\frac{\pi }{2}} \right]} f\left( {\sin x} \right) = 5.\) |
|
|
| ||
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ sau:
![Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759149338.png)
Khẳng định | Đúng | Sai | |
a) | \(\mathop {\max }\limits_{x \in \left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right).\) |
|
|
b) | \(\mathop {\min }\limits_{x \in \left[ { - 1;3} \right]} f\left( x \right) = - 2.\) |
|
|
c) | Tập giá trị của hàm số \(f\left( x \right)\)trên \(\left[ { - 1;2} \right]\) là \(\left[ { - 2;3} \right]\) |
|
|
d) | \(\mathop {\max }\limits_{x \in \mathbb{R}} f\left( {3{{\sin }^2}x - 1} \right) = 2.\) |
|
|
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Giá trị nhỏ nhất của hàm số \(y = {x^2} + \frac{2}{x}\) trên đoạn \(\left[ {\frac{1}{2};2} \right]\) là…
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(g(x) = \frac{{\ln x}}{x}\) trên đoạn \([1;4]\) là… (làm tròn đến hàng trăm)
Giá trị lớn nhất của hàm số \(f\left( x \right) = \sin x + \cos 2x\) trên \(\left[ {0;\pi } \right]\) là …
Một màn hình \(BC\) có chiều cao \(1,4m\) được đặt thẳng đứng và mép dưới của màn hình cách mặt đất một khoảng \(BA = 1,8m\). Một chiếc đèn quan sát màn hình được đặt ở vị trí \(O\) trên mặt đất. Hãy xác định khoảng cách \(AO\) sao cho góc quan sát \(BOC\) là lớn nhất.

Một ông nông dân có \(240\)m hàng rào và muốn rào lại cánh đồng hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được cánh đồng với diện tích lớn nhất là………
Anh Hà dự định làm một cái thùng đựng dầu hình trụ bằng sắt có nắp đậy thể tích \(10\,{m^3}\). Chi phí làm mỗi \({m^2}\) đáy là 400 ngàn đồng, mỗi \({m^2}\) nắp là 200 ngàn đồng, mỗi \({m^2}\) mặt xung quanh là 300 ngàn đồng. Để chi phí làm thùng là ít nhất thì anh Hà cần chọn chiều cao của thùng là……………………….. (Xem độ dày của tấm sắt làm thùng là không đáng kể, làm tròn kết quả đến hàng phần trăm).