Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 2
21 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
[1] Xét các khẳng định sau:
(I) Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(m\) thì có số thực \({x_1}\) thỏa mãn \(f\left( {{x_1}} \right) = m\) và \(f\left( x \right) > m,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_1}} \right\}\).
(II) Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(m\) thì có số thực \({x_1}\) thỏa mãn \(f\left( {{x_1}} \right) = m\) và \(f\left( x \right) \ge m,\forall x \in \left( { - \infty ; + \infty } \right)\).
(III) Nếu giá trị lớn nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(M\) thì có số thực \({x_2}\) thỏa mãn \(f\left( {{x_2}} \right) = M\) và \(f\left( x \right) < M,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_2}} \right\}\).
Số khẳng định đúng là
\(0\).
\(1\).
\(2\).
\(3\).
Giá trị lớn nhất của hàm số \(y = \left( {x + 3} \right)\left( { - x + 3} \right)\) bằng
\(0\).
\( - 9\).
\(9\).
\(3\).
Giá trị lớn nhất của hàm số có đồ thị như hình là 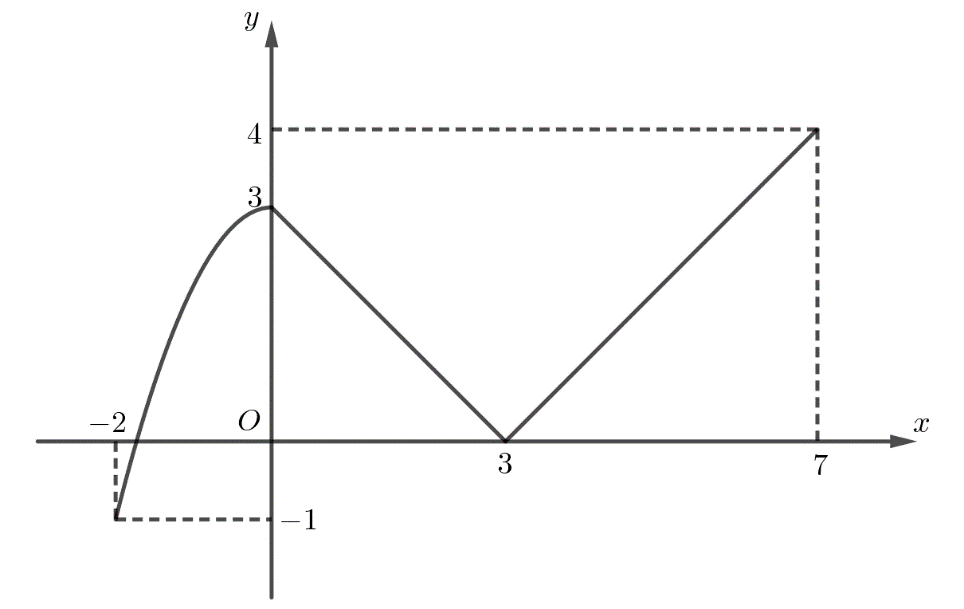
\(3\).
\(7\).
\( - 1\).
\(4\).
Cho hàm số \(y = f(x)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1\,;\,3} \right]\) như hình vẽ bên. Khẳng định nào sau đây đúng?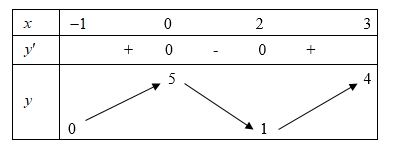
\(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f(x) = f(0)\).
\(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
\(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
\(\mathop {\max }\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2\,;\,2} \right]\).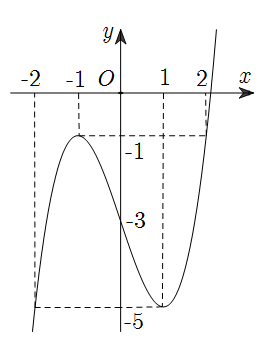
\(m = - 5\,;\,M = - 1\).
\(m = - 2\,;\,M = 2\).
\(m = - 1\,;\,M = 0\).
\(m = - 5\,;\,M = 0\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như hình vẽ. Hãy chọn khẳng định đúng?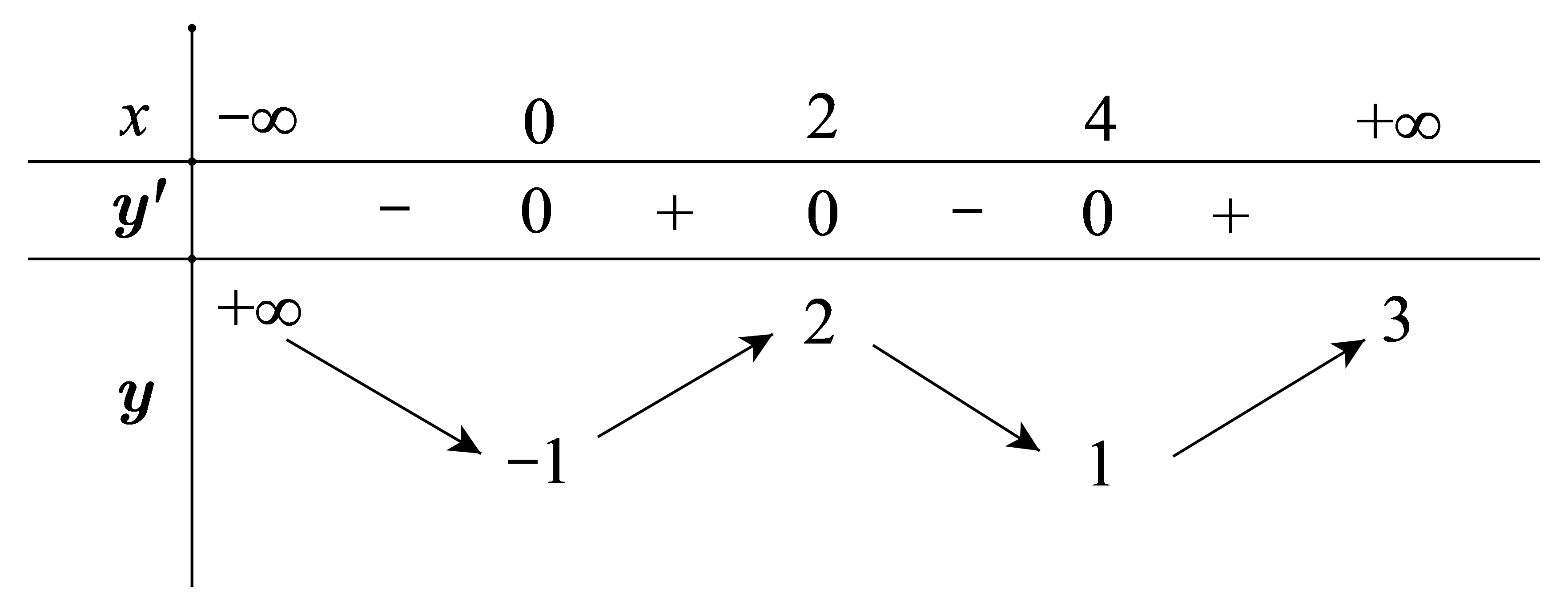
Hàm số có giá trị lớn nhất bằng 3 và giá trị nhỏ nhất bằng \[ - 1\].
Hàm số có giá trị lớn nhất bằng 3 và giá trị nhỏ nhất bằng \[1\].
Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng \[ - 1\].
Không tồn tại giá trị lớn nhất của hàm số.
Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn \(\left[ {2\,;\,4} \right]\) là
\(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = 6\).
\(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = \frac{{13}}{2}\).
\(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = \frac{{25}}{4}\).
\(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = - 6\).
Tìm \(x\) để hàm số \(y = \sqrt {x + 1} + \sqrt {6 - x} \) đạt giá trị lớn nhất.
\(x = 6\).
\(x = 0\).
\(x = - 1\).
\(x = \frac{5}{2}\).
Giá trị lớn nhất của hàm số \(y = {\cos ^4}x - {\cos ^2}x + 4\) bằng
5.
\(\frac{1}{2}\).
4.
\(\frac{{17}}{4}\).
Gọi \(M,\)\(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{x + 1}}{{x - 1}}\) trên đoạn \(\left[ {3\,;\,5} \right].\) Khi đó \(M - m\) bằng
2.
\(\frac{3}{8}\).
\(\frac{7}{2}\).
\(\frac{1}{2}\).
Gọi \(m\) và \(M\) lần lượt là các giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = {e^{2 - 3x}}\) trên đoạn \(\left[ {0\,;\,2} \right].\) Mối liên hệ giữa \(M\) và \(m\) là
\(M - m = e\).
\(m + M = 1\).
\(m.M = \frac{1}{{{e^2}}}\).
\(\frac{M}{m} = {e^2}\).
Giá trị lớn nhất của hàm số \[y = {\log _2}\left( {{x^2} + 4} \right)\] trên đoạn \[\left[ { - 2;\,5} \right]\] là
\(3\).
\(2\).
\({\log _2}29\).
\(5\).
PHẦN II. Câu trắc nghiệm đúng sai
Cho hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\), với \(m\) là tham số.
a) [1] Nếu đồ thị của hàm số \(y = {x^3} - 3{x^2} + m\) luôn cắt trục hoành thì giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) bằng 0.
b) [2] Với \(m = 2\), giá trị nhỏ nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {3;\,\,5} \right]\) bằng 2.
c) [2] Với \(m < 0\), giá trị lớn nhất của hàm số \(y = \left| {{x^3} - 3{x^2} + m} \right|\) trên đoạn \(\left[ {0;\,\,1} \right]\)bằng \(m\).
d) [3] Biết hàm số \(y = f\left( x \right) = \left| {{x^3} - 3{x^2} + m} \right|\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 2;\,\,2} \right]\) bằng 10. Khi đó tổng các giá trị của tham số \(m\) là \(30\).
Cho hàm số \(y = \left| {{x^4} - 2{x^2} + 3m} \right|\) với \(m\) là tham số. Xác định tính đúng sai của các mệnh đề sau
a) [1] Khi \(m = 1\) giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;2} \right]\) bằng 2.
b) [2] Khi \(m = 1\) giá trị lớn nhất của hàm số trên đoạn \(\left[ {0;2} \right]\) bằng 4.
c) [2] Để giá trị lớn nhất trên \(\left[ { - 1;1} \right]\) bằng 9 thì có hai giá trị của tham số \[m\].
d) [3] Biết rằng có đúng hai giá trị \({m_1},{m_2}\) của \(m\) để giá trị nhỏ nhất của hàm số đã cho trên \(\left[ { - 1;2} \right]\) bằng 2024. Khi đó \(3\left| {{m_1} - {m_2}} \right| = 4057\).
Cho hàm số \(f(x) = {e^{2x}} - 4{e^x} + m\). Xác định tính đúng sai của các mệnh đề sau
a) [1] Khi \[m = 1\]giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0\,;\,\ln 4} \right]\) bằng \[ - 3\].
b) [2] Khi \[m = 1\]giá trị lớn nhất của hàm số trên đoạn \(\left[ {0\,;\,\ln 4} \right]\) bằng \[ - 2\].
c) [2] Để giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0\,;\,\ln 4} \right]\) bằng 5 thì \[m = 9\].
d) [3] Có hai giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số\(y = \left| {f(x)} \right|\) trên đoạn \(\left[ {0\,;\,\ln 4} \right]\) bằng\(6\).
Cho hàm số \(y = f\left( x \right)\). Biết bảng xét dấu của \(f'\left( x \right)\) như sau
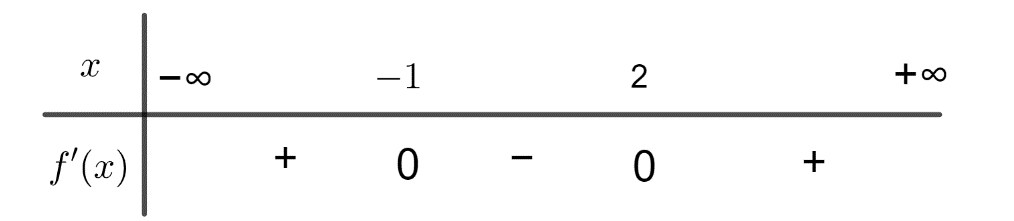
Các khẳng định sau đúng hay sai?
a) [1] Giá trị lớn nhất của hàm số \[y = f(x)\]trên đoạn \[\left[ { - 1;2} \right]\] là \[f( - 1)\].
b) [2] Giá trị nhỏ nhất của hàm số \[y = f(x)\]trên đoạn \[\left[ { - 1;3} \right]\] là \[f(3)\].
c) [2] Giá trị lớn nhất của hàm số \[h\left( x \right) = f(2x)\]trên đoạn \[\left[ { - 1;1} \right]\] là \[f( - 1)\].
d) [3] Giá trị lớn nhất của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right) - 3{x^2} + 6x - 5\) trên \(\left[ {0;2} \right]\) là \(f\left( 0 \right) - 2\).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Hàm số \(f(x) = {x^3} - 3{x^2} + 4x + {m^2} - 2m\) có giá trị lớn nhất trên \(\left( {0;1} \right]\) là \(M\) thỏa mãn \(M \le 8\). Số các giá trị nguyên của tham số \(m\)là
Tìm giá trị nhỏ nhất của hàm số \(y = f\left( x \right) = \cos x\left( {1 - 2\cos 2x} \right)\).
Người ta muốn sản xuất một bể nước theo dạng khối lăng trụ tứ giác đều, không có nắp trên, làm bằng kính và có thể tích là \(16{m^3}\). Biết giá của mỗi mét vuông kính là \(500\,000\)đồng. Tìm số tiền tối thiểu phải trả để làm bể nước trên (làm tròn đến hàng đơn vị).
Từ hình vuông có cạnh bằng \[6\] người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp bằng 
Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Diện tích lớn nhất của đất rào thu được là