Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 1
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Cho hàm số \(y = f\left( x \right)\)liên tục trên \[\mathbb{R}\]thỏa mãn giá trị nhỏ nhất của hàm số trên \[\mathbb{R}\]là \(5\). Khẳng định nào sau đây là đúng?
\(f\left( x \right) > 5\)\[\forall x \in \mathbb{R}\].
\[f\left( x \right) \ge 5\]\[\forall x \in \mathbb{R}\], \[\exists {x_0}\], \[f\left( {{x_0}} \right) = 5\].
\(f\left( x \right) < 5\)\[\forall x \in \mathbb{R}\].
\[f\left( x \right) \le 5\]\[\forall x \in \mathbb{R}\], \[\exists {x_0}\], \[f\left( {{x_0}} \right) = 5\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên đoạn \(\left[ {0;3} \right]\) như sau:
![Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên đoạn \(\left[ {0;3} \right]\) như sau: Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) là A. \(4\). B. \(1\). C. \(0\). D. \( - \;4\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759142765.png)
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) là
\(4\).
\(1\).
\(0\).
\( - \;4\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ sau
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ sau Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \[\left[ { - 1;2} \right]\] là A. \[3\]. B. \[ - 1\]. C. \[1\]. D. \[2\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759142817.jpg)
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \[\left[ { - 1;2} \right]\] là
\[3\].
\[ - 1\].
\[1\].
\[2\]
Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có bảng biến thiên như sau:
![Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có bảng biến thiên như sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759142970.png)
Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\). Khi đó giá trị của \(M - m\) là
\(M - m = 5.\)
\(M - m = 4.\)
\(M - m = 6\).
\(M - m = 3\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;5} \right]\) và có đồ thị như hình vẽ sau:
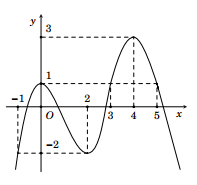
Khẳng định nào sau đây đúng?
\[\mathop {Max}\limits_{\left[ { - 1;5} \right]} f\left( x \right) = 2\].
\[\mathop {Min}\limits_{\left[ {3;5} \right]} f\left( x \right) = - 2.\]
\[\mathop {Max}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 3.\]
\[\mathop {Max}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = 1.\]
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.
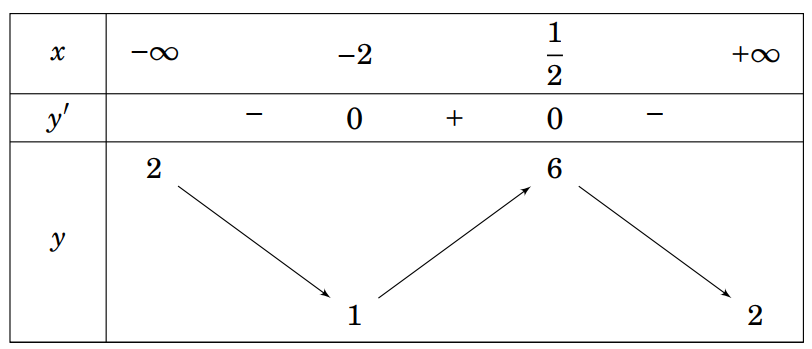
Chọn khẳng định đúng trong các khẳng định sau:
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ; - 2} \right)\) là \(1\) .
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\) là \(6\).
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - 2;\frac{1}{2}} \right)\) là \(1\).
Hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất trên khoảng \(\left( { - 2; + \infty } \right)\).
Giá trị lớn nhất của hàm số \(y = \frac{{{x^2}}}{{x + 1}}\) trên đoạn \(\left[ {0;2} \right]\) là
\(1\).
\(0\).
\( - \frac{4}{3}\).
\(\frac{4}{3}\).
Giá trị nhỏ nhất của hàm số \(y = \sqrt {x + 1} \) trên tập xác định là
\(1\).
\(0\).
\( - 1\).
\(\sqrt 2 \).
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \sin 2x + 2\) trên tập xác định là
\(4\).
\(0\).
\(3\).
\(1\).
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{x - 2}}{{x + 1}}\) trên \(\left( { - 1; + \infty } \right)\) .
Không tồn tại.
\(\mathop {\max }\limits_{\left( { - 1;\, + \infty } \right)} f\left( x \right) = 2\).
\(\mathop {\max }\limits_{\left( { - 1;\, + \infty } \right)} f\left( x \right) = - 1\).
\(\mathop {\max }\limits_{\left( { - 1;\, + \infty } \right)} f\left( x \right) = 1\).
Tìm giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left( {x - 3} \right){e^{2x}}\).
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - \frac{{{e^5}}}{2}\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = \frac{{{e^5}}}{2}\].
\[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = {e^5}\].
Không tồn tại.
Gọi giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{\ln x}}{x}\) trên nửa khoảng \(\left[ {1;\,{e^2}} \right)\) lần lượt là \(m\) và \(M\). Giá trị của biểu thức \(\ln \left( {m + M} \right)\)bằng
\[1\].
\[ - 1\].
\[e\].
\({e^{ - 1}}\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Cho hàm số \(y = \left| {{x^3} + 3{m^2}x + 2} \right|\), với \(m\) là tham số
a) Hàm số \(f\left( x \right) = {x^3} + 3{m^2}x + 2\) luôn có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn \(\left[ {0;1} \right]\) với mọi giá trị của \(m\).
b) Khi \(m = 0\), giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;1} \right]\) bằng \(y\left( 1 \right)\).
c) Khi \(m = 1\), trên đoạn \(\left[ { - 2;0} \right]\) hàm số có giá trị lớn nhất bằng 2 và đạt giá trị nhỏ nhất tại \(x = 0\)
d) Tổng tất cả các giá trị của tham số \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} y = 5\) là \(\frac{2}{3}\).
Cho hàm số \(y = f(x) = \left| {{x^4} - 2{x^2} + 2m - 3} \right|\)
a) Khi \(m = 2\) giá trị nhỏ nhất của hàm số bằng \(5\).
b) Khi \(m = 3\) giá trị lớn nhất của hàm số trên đoạn \(\left[ {0;3} \right]\) bằng \(15\)
c) Có 2 giá trị của \(m\) để hàm số đạt giá trị lớn nhất trên đoạn \(\left[ { - 1;0} \right]\) bằng \(27\)
d) Tổng tất cả các giá trị của \(m\) để \(\mathop {\max }\limits_{\left[ { - 1;0} \right]} f(x) + \mathop {\min }\limits_{\left[ { - 1;0} \right]} f(x) = 3\) bằng \(\frac{7}{2}\)
Cho hàm số \(y = f\left( x \right) = {\log _2}\left( {{x^2} - 3x + 2} \right)\)
a) Hàm số có giá trị lớn nhất trên khoảng \(\left( {2; + \infty } \right)\).
b) Hàm số luôn có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn \(\left[ { - 1;0} \right]\).
c) Trên đoạn \(\left[ { - 1;0} \right]\) hàm số có giá trị nhỏ nhất bằng 1.
d) Gọi \({m_0}\) là giá trị của tham số \(m\) để hàm số \(g\left( x \right) = {2^{f\left( x \right)}} + m\) có giá trị nhỏ nhất trên đoạn \(\left[ {3;4} \right]\) bằng \( - 3\). Khi đó \({m_0} \in \left( { - 5;0} \right)\).
Cho hàm số \(y = f(x) = {x^3} - 3x + {m^2} - 2\) .
a) Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 1;1} \right]\) bằng \( - 4\) khi \(m = 0\).
b) Giá trị nhỏ nhất của hàm số \(y = f(2x)\) trên đoạn \(\left[ { - \frac{1}{2};\frac{1}{2}} \right]\) bằng \( - 4\) khi \(m = 0\).
c) Giá trị lớn nhất của hàm số \(y = f(x + 1)\) trên đoạn \(\left[ { - 3;0} \right]\) bằng \(1\) khi \(m = 1\).
d) Có \(2024\) giá trị của nguyên của \(m \in \left( { - 2023;2024} \right)\) để giá trị nhỏ nhất của hàm số \(h(x) = f(1 - 3x)\) trên đoạn \(\left[ { - 2;0} \right]\) nhỏ hơn \(2\).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hàm số \(f\left( x \right) = {x^3} - 3m{x^2} + 10\), trong đó \(m\) là số nguyên dương. Tìm \(m\) để giá trị nhỏ nhất của hàm số trên nửa khoảng \(\left[ {0; + \infty } \right)\) bằng \(6\).
Giá trị lớn nhất của hàm số \[y = \frac{1}{3}{\cos ^3}x + \frac{1}{4}\cos 2x - 2\cos x + \frac{5}{4}\] trên đoạn là \(\frac{m}{n}\) (với \(m,\,n\) là hai số nguyên dương và nguyên tố cùng nhau). Khi đó kết quả của \(m - 3n\) bằng bao nhiêu?
Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng \[200\,{m^3}\]. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 350 nghìn đồng/\[{m^2}\]. Hãy xác định chi phí thấp nhất để xây bể (làm tròn đến đơn vị triệu đồng).
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông cạnh \(x\,\left( {cm} \right)\), chiều cao \(h\,\left( {cm} \right)\) và diện tích bề mặt bằng \[108\,c{m^2}\] như hình dưới đây. Tìm chiều cao \(h\,\left( {cm} \right)\) sao cho thể tích của hộp là lớn nhất.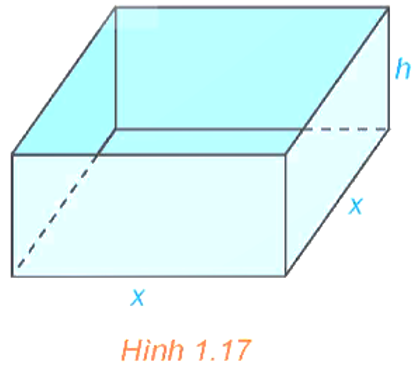
Ông A muốn mua một mảnh đất hình chữ nhật có diện tích bằng \(100\,{m^2}\)để làm khu vườn. Để chi phí xây dựng bờ rào xung quanh khu vườn là ít tốn kém nhất thì ông A đã mua mảnh đất có kích thước \(a(m)\, \times \,b(m)\)(với \(a\) là chiều dài, \(b\) là chiều rộng của khu vườn). Khi đó kết quả của \(a + 2b\) bằng bao nhiêu?
Một doanh nghiệp tư nhân chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung vào chiến lược kinh doanh xe X với chi phí mua vào một chiếc là \(30\) triệu đồng và bán ra với giá \(35\) triệu đồng. Với giá bán này, số lượng xe mà khách hàng đã mua trong một năm là \(400\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe X đang bán, doanh nghiệp dự định giảm giá bán. Bộ phận nghiên cứu thị trường ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm sẽ tăng thêm \(100\) chiếc. Hỏi theo đó, giá bán mới là bao nhiêu thì lợi nhuận thu được cao nhất?