Đề kiểm tra Biểu thức tọa độ của các phép toán vecto (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Trong không gian \(Oxyz\), cho 2 điểm \(A\left( {1;2;3} \right)\), \(B\left( { - 1;1; - 1} \right)\). Gọi \(I\) là trung điểm của đoạn thẳng \(AB\), tọa độ điểm \(I\) là
\(I\left( {0;\frac{3}{2}; - 1} \right)\).
\(I\left( {0;3;2} \right)\).
\(I\left( {2;\frac{5}{2};5} \right)\).
\(I\left( {0;\frac{3}{2};1} \right)\).
Trong không gian\(Oxyz\), cho tam giác \(\Delta ABC\) có \(A\left( {1; - 1;2} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( {2;3;1} \right)\). Gọi \(G\)là trọng tâm tam giác \(\Delta ABC\), tọa độ điểm \(G\) là
\(G\left( {\frac{5}{3};\frac{1}{3}; - 2} \right)\).
\(G\left( {\frac{5}{2};\frac{1}{2};3} \right)\).
\(G\left( {5;1;6} \right)\).
\(G\left( {\frac{5}{3};\frac{1}{3};2} \right)\).
Trong không gian\(Oxyz\), cho tam giác \(\Delta ABC\) có \(A\left( {0; - 1;4} \right)\), \(B\left( {1; - 1;0} \right)\). Tìm tọa độ điểm \(C\) để điểm \(G\left( { - 2;0;1} \right)\) là trọng tâm \(\Delta ABC\)?
\[C\left( {7; - 2;1} \right)\].
\[C\left( {7;2; - 1} \right)\].
\[C\left( { - 7;2;1} \right)\].
\[C\left( { - 7;2; - 1} \right)\].
Trong không gian \[Oxyz\], cho \[\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \], \[\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j + {z_2}\overrightarrow k \]. Khẳng định nào sau đây là đúng?
![Trong không gian \[Oxyz\], cho \[\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \], (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/3-1759372464.png){kind=small}
![Trong không gian \[Oxyz\], cho \[\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \], (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/10/4-1759372473.png){kind=small}
![Trong không gian \[Oxyz\], cho \[\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \], (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/10/5-1759372483.png){kind=small}
![Trong không gian \[Oxyz\], cho \[\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \], (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/10/6-1759372492.png){kind=small}
Trong không gian \[Oxyz\], cho \(\overrightarrow a = \left( {1; - 2;3} \right)\) và \(\overrightarrow b = \left( {2; - 1; - 1} \right)\). Vecto tích có hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \)có độ dài bằng
\[15\].
\(\sqrt {83} \).
\(83\).
\(\sqrt {15} \).
Trong không gian \[Oxyz\], cho hai vectơ \[\overrightarrow u \left( {2;2;3} \right)\] và \[\overrightarrow v \left( {5;2;0} \right)\]. Khi đó \(\left[ {\overrightarrow u ,\,\overrightarrow v } \right]\) bằng
\(\left( {2;\, - 5;\,2} \right)\).
\(\left( {6;\, - 15;\,6} \right)\).
\(\left( { - 6;\,15;\, - 6} \right)\).
\(\left( { - 2;\,5;\, - 2} \right)\).
Trong không gian \[Oxyz\], cho hai vectơ \[\overrightarrow u \left( {3; - 2;1} \right)\], \[\overrightarrow v \left( {0;1; - 1} \right)\]. Khẳng định nào sau đây sai?
\(\overrightarrow u .\overrightarrow v = - 3\).
\(\left| {\overrightarrow u + \overrightarrow v } \right| = \sqrt {10} \).
\(\left| {\overrightarrow u } \right| = \sqrt {14} \).
\(\left| {\overrightarrow v } \right| = 2\).
Trong không gian \[Oxyz\],cho \(\overrightarrow a = \left( {3;2;1} \right)\), \(\overrightarrow b = \left( { - 2;0;1} \right)\). Độ dài của \(\overrightarrow a + \overrightarrow b \) là
\(3\).
\(1\).
\(2\).
\(\sqrt 2 \).
Trong không gian \[Oxyz\], cho các vectơ \(\overrightarrow a = \left( {1;\, - 1;\,2} \right)\), \(\overrightarrow b = \left( {3;\,0;\, - 1} \right)\) và \(\overrightarrow c = \left( { - 2;\,5;\,1} \right)\). Toạ độ của vectơ \(\overrightarrow u = \overrightarrow a + \overrightarrow b - \overrightarrow c \) là
\(\overrightarrow u = \left( { - 6;\,6;\,0} \right)\).
\(\overrightarrow u = \left( {6;\, - 6;\,0} \right)\).
\(\overrightarrow u = \left( {6;\,0;\, - 6} \right)\).
\(\overrightarrow u = \left( {0;\,6;\, - 6} \right)\).
Trong không gian \[Oxyz\], cho hai điểm \(A\left( {4;\,\,2;\,\,1} \right)\), \(B\left( { - 2;\, - 1;\,4} \right)\). Tìm tọa độ điểm \(M\)thỏa mãn đẳng thức \(\overrightarrow {AM} = 2\overrightarrow {MB} \).
\(M(0;0; - 3)\).
\(M( - 8; - 4;7)\).
\(M(8;{\mkern 1mu} {\mkern 1mu} 4; - 7)\).
\(M\left( {0;0;3} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai vectơ\[\overrightarrow u \left( {1;0; - 3} \right)\] và \[\overrightarrow v \left( {1;3; - 2} \right)\]. Khi đó tọa độ của một vectơ vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là
\(\left( { - 3;\,1;\, - 9} \right)\).
\(\left( {3;9; - 1} \right)\).
\(\left( {9;\,1;\, - 3} \right)\).
\(\left( { - 9;\,1;\, - 3} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho\[\alpha \]là góc giữa hai vectơ\[\overrightarrow a \left( { - 1;2;1} \right)\], \[\overrightarrow v \left( {4; - 1; - 2} \right)\]. Khẳng định nào sau đây sai?
\(\sin \alpha .\;{\rm{co}}{\rm{s}}\alpha = - \frac{{4\sqrt {62} }}{{63}}\).
\(\sin \alpha = \frac{{\sqrt {217} }}{{21}}\).
\({\rm{co}}{\rm{s}}\alpha = \frac{{ - 4\sqrt {14} }}{{21}}\).
\({\rm{co}}{\rm{s}}\alpha = \frac{{4\sqrt {14} }}{{21}}\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Trong không gian \(Oxyz,\) cho vectơ \(\vec a = \left( {2; - 2; - 4} \right),\,\,\vec b = \left( {1;1;2} \right).\)
a) \(\vec a + \vec b = \left( {3; - 3; - 3} \right)\) .
b) \(\vec a\) và \(\vec b\) cùng phương .
c) \(\left| {\vec b} \right| = \sqrt 3 \).
d) \(\vec a = 2\overrightarrow i - 2\overrightarrow j - 4\overrightarrow k \).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {2;3; - 4} \right)\), \(B\left( { - 1;1;0} \right)\), \(C\left( { - 1;3; - 1} \right)\).
a) Tam giác \(ABC\) là tam giác vuông.
b) Với điểm \(D\left( {a;b;c} \right)\) thỏa mãn tứ giác\(ABCD\) là hình chữ nhật thì \(a + b + c = 9\).
c) \(\sin \widehat {BAC} = \sqrt {\frac{{57}}{{58}}} \)
d) Với điểm \(M\left( {1;m;n} \right)\) thỏa mãn \(A,B,M\) thẳng hàng thì \(m + n = - 3.\)
Trong không gian \(Oxyz\), cho hình hộp\(ABCD.A'B'C'D'\) có\(A(0;0;0)\)\(\;B(3;0;0)\)\(D\left( {0;3;0} \right);\)\(D'\left( {0;3; - 3} \right)\).
a) Tọa độ điểm \(C\) là \(C\left( { - 3; - 3;0} \right)\).
b) Tọa độ trọng tâm tam giác \(A'B'C\) là \(G\left( {2;1; - 2} \right)\).
c) Góc giữa hai đường thẳng \(AC\) và \(B'G\)là \(60^\circ \).
d)Thể tích khối hộp đã cho là \(3\)(đvtt).
Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ Oxyz được gắn như hình vẽ, trong đó gốc \(O\) là vị trí của trạm kiểm soát không lưu và \(M\left( {x;y;z} \right)\) (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí \(\left( {50;120;4} \right)\) và chuyển động với vận tốc \(\vec v = \left( {300;400;3} \right)\) (km/h)
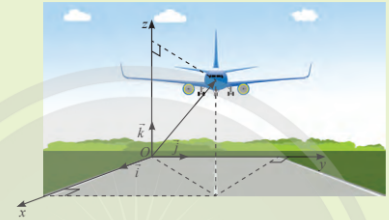
a) Tại thời điểm 8h, khoảng cách giữa máy bay và trạm kiểm soát không lưu nói trên xấp xỉ 130 km (sai số không quá 1km).
b) Tại thời điểm 9h độ cao của máy bay so với mặt đất là 8km.
c) Tại thời điểm 10h, khoảng cách giữa máy bay và một tháp truyền hình \(F\) có tọa độ \(\left( {1250;1020;0} \right)\) xấp xỉ 700km (sai số không quá 10km).
d) Khi đạt độ cao 10km, máy bay đổi vận tốc mới là \(\overrightarrow {{v_2}} = \left( {400;300; - 5} \right)\)để hướng đến sân bay \(B\). Tọa độ của máy bay khi vừa đáp xuống sân bay \(B\) là \(\left( {1450;1520;0} \right)\).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Trong không gian với hệ tọa độ \(Oxyz\), cho hình vuông \(ABCD\) với \[B\left( {3;0;8} \right)\], \[D\left( { - 5; - 4;0} \right)\], \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = a\sqrt b \). Tính giá trị biểu thức \(M = a + 2b\).
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là \(10\)m, chiều rộng là \(8\)m và chiều cao là \(4\)m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với một góc phòng và mặt phẳng \((Oxy)\) trùng với mặt sàn, đơn vị đo được lấy theo mét (Hình vẽ).
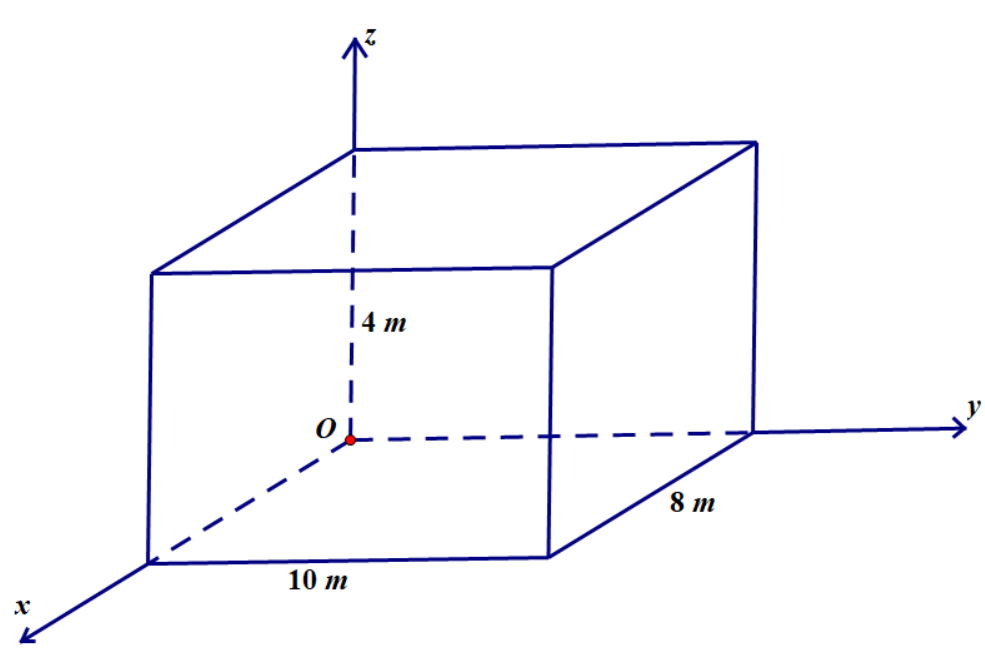
Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm).
Một em nhỏ cân nặng \[20kg\] trượt trên cầu trượt dài 3m. Biết rằng cầu trượt có góc nghiêng so với phương nằm ngang là \[{30^ \circ }\]. Cho biết công A(J) sinh bởi một lực \[\overrightarrow F \] có độ dịch chuyển \[\overrightarrow d \]được tính bởi công thức \[A = \overrightarrow {F.} \overrightarrow d \]. Hãy tính công sinh bởi trọng lực \[\overrightarrow P \]khi em nhỏ trượt hết chiều dài cầu trượt biết gia tốc rơi tự do \[g = 9,8\,m/{s^2}\].![Ta có: \[\left| {\overrightarrow P } \right| = P = m.g = 20.9,8 = 196(N)\]. \[\left| {\overrightarrow d } \right| = \left| {\overrightarrow {AC} } \right| = AC = 3(m)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/19-1759368263.png)
Cho hình lập phương \[ABCD.A'B'C'D'\]có cạnh bằng \[a\]. Gọi \[M\] là trung điểm của \[D'C'\] và \[G\] là trọng tâm \[\Delta A'D'C'\] . Tính tích vô hướng của hai vectơ \[\overrightarrow {AC'} \] và \[\overrightarrow {A'G} \].
Trong không gian \[Oxyz\], cho tứ diện \[ABCD\] có \[A\left( {2;0;0} \right),\,\,B\left( { - 2;3;0} \right),\,\,C\left( {2;3;0} \right)\]. Điểm \[D\] nằm trên trục \[Oz\] sao cho có thể tích khối tứ diện \[ABCD\] bằng \[128\]. Tính tổng cao độ các điểm \[D\].
Trong không gian với hệ tọa độ \(Oxyz\), cho hình thang \(ABCD\) có hai đáy \(AB\), \(CD\); có tọa độ ba đỉnh \(A\left( {1;2;1} \right)\), \(B\left( {2;0; - 1} \right)\), \(C\left( {6;1;0} \right)\). Biết hình thang có diện tích bằng \(6\sqrt 2 \). Giả sử đỉnh \(D\left( {a;b;c} \right)\). Tính tổng \(S = a + b + c.\)
