Đề kiểm tra Biểu thức tọa độ của các phép toán vecto (có lời giải) - Đề 1
22 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN CHỌN
Trong không gian \[Oxyz\], cho vectơ \(\overrightarrow a \) biểu diễn của các vectơ đơn vị là \(\overrightarrow a = 2\overrightarrow i + \overrightarrow k - 3\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
\[\left( {1;\,2;\, - 3} \right)\].
\[\left( {2;\, - 3;\,1} \right)\].
\[\left( {2;\,1;\, - 3} \right)\].
\(\left( {1;\, - 3;\,2} \right)\).
Cho hình hộp \(ABCD.\,A'B'C'D'\). Chọn đẳng thức vectơ đúng:
\(\overrightarrow {DB'} = \overrightarrow {DA} + \overrightarrow {DD'} + \overrightarrow {DC} \).
\(\overrightarrow {AC'} = \overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {AD} \).
\(\overrightarrow {DB} = \overrightarrow {DA} + \overrightarrow {DD'} + \overrightarrow {DC} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AB'} + \overrightarrow {AD} \).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;{\rm{ }} - 1;{\rm{ }}2} \right)\) và \(B\left( {2;{\rm{ }}1;{\rm{ }}1} \right)\). Độ dài đoạn thẳng\(AB\) bằng
\(2\).
\(\sqrt 6 \).
\(\sqrt 2 \).
\(6\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec u\left( {{x_1};{y_1};{z_1}} \right)\)và \(\vec v\left( {{x_2};{y_2};{z_2}} \right)\). Trong các khẳng định sau, khẳng định đúng là
\(\vec u + \vec v = \left( {{x_1}.{x_2};{y_1}.{y_2};{z_1}.{z_2}} \right)\).
\(\vec u + \vec v = \left( {{x_1} - {x_2};{y_1} - {y_2};{z_1} - {z_2}} \right)\).
\(\vec u + \vec v = \left( {{y_1} + {y_2};{x_1} + {x_2};{z_1} + {z_2}} \right)\).
\(\vec u + \vec v = \left( {{x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2}} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( {3;1; - 3} \right)\)và\(B\left( {0; - 2;1} \right)\). Tọa độ trung điểm của đoạn thẳng\(AB\) là
\(M\left( {1;2; - 1} \right)\).
\(N\left( {\frac{3}{2}; - \frac{1}{2}; - 1} \right)\).
\(P\left( {\frac{3}{2};\frac{1}{2};1} \right)\).
\(K\left( {3; - 1; - 2} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và\(\vec b\left( {1;2; - 1} \right)\). Tọa độ của vectơ \(\vec c = \vec a - \vec b\) là
\(\left( { - 1;0; - 2} \right)\).
\(\left( { - 2; - 2;4} \right)\).
\(\left( {2;2; - 4} \right)\).
\(\left( {0;2;2} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow u = \left( {1; - 1; - 1} \right)\)và\(\overrightarrow v = \left( {0; - 3;3} \right)\). Góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng
\(45^\circ \).
\(30^\circ \).
\(60^\circ \).
\(90^\circ \).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( {2;1; - 1} \right)\)và\(B\left( { - 1;1;3} \right)\). Độ dài đoạn thẳng\(AB\) là
\(5\).
\(7\).
\(\sqrt {29} \).
\(4\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và \(\vec b\left( {1;2; - 1} \right)\). Vectơ vuông góc với cả hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)là
\(\vec c\left( { - 6; - 2; - 2} \right)\).
\(\vec d\left( {3; - 1;1} \right)\).
\(\vec m\left( { - 3; - 1;1} \right)\).
\(\vec n\left( {2;1;4} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {4; - 3; - 1} \right)\)và\(\overrightarrow b = \vec i + 2\vec j + \vec k\). Tìm tọa độ của \(2\vec a + 3\vec b\)
\(\left( {11;0;1} \right)\).
\(\left( {5; - 1;0} \right)\).
\(\left( {11;0; - 1} \right)\).
\(\left( {5; - 1; - 1} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A\left( { - 1; - 1;3} \right)\), \(B\left( {0;2;0} \right)\)và \(C\left( {5; - 2;1} \right)\). Tìm tọa độ của điểm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành
\(\left( { - 4; - 5;4} \right)\).
\(\left( {4; - 5;4} \right)\).
\(\left( {4;5; - 4} \right)\).
\(\left( { - 4; - 5; - 4} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba điểm \(A\left( { - 1; - 1;3} \right)\), \(B\left( {0;2;0} \right)\)và \(C\left( {5; - 2;1} \right)\). Chu vi của tam giác \(ABC\) là?
\(\sqrt {19} + 2\sqrt {41} \).
\(\sqrt {19} + \sqrt {41} + \sqrt {42} \).
\(\sqrt {19} + 2\sqrt {42} \).
\(\sqrt {19} + \sqrt {41} + \sqrt {43} \).
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
Trong không gian với hệ trục tọa độ Oxyz, cho \(A\left( {1; - 1;2} \right)\), \(B\left( { - 2;0;3} \right)\), \(C\left( {0;1; - 2} \right)\). Các mệnh đề sau đúng hay sai?
a) Tọa độ trọng tâm tam giác \(ABC\) là \(G\left( {\frac{{ - 1}}{3};0;1} \right)\).
b) Độ dài đoạn thẳng \(AB = \sqrt {11} \).
c) Tích có hướng \([\overrightarrow {AB} ,\,\overrightarrow {AC} ] = \left( { - 6;13; - 5} \right)\).
d) \(M\left( {a;b;c} \right)\)là điểm thuộc mặt phẳng \[\left( {Oxy} \right)\] sao cho biểu thức \[S = 2.\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MB} .\overrightarrow {MC} + \overrightarrow {MC} .\overrightarrow {MA} \] đạt giá trị nhỏ nhất. Khi đó biểu thức \[T = a - b + c = \frac{1}{4}\].
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \[A\left( {1;2;0} \right),B\left( {0;1;1} \right),C\left( {2;1;0} \right)\].
a) Tam giác \(ABC\) vuông tại \(A.\)
b) Chu vi tam giác là \(\sqrt 7 + \sqrt 3 + \sqrt 2 .\)
c) Diện tích tam giác \(ABC\)là \(\sqrt 6 .\)
d) Tâm đường tròn ngoại tiếp tam giác \(ABC\)là \(I\left( {1;1;\frac{1}{2}} \right).\)
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \[A\left( { - 2;0; - 3} \right),B\left( { - 4;1; - 1} \right),C\left( { - 4; - 4;1} \right)\].
a) Góc \(A\) là góc nhọn.
b) Toạ độ điểm \(D\) đối xứng với \(A\) qua \(B\) là \(\left( { - 6;2;1} \right)\).
c) Độ dài đường phân giác trong góc \(A\) là \(\frac{{\sqrt {26} }}{3}\).
d) Gọi \(M\left( {a;b;c} \right)\) thuộc mặt phẳng \(\left( {Oyz} \right)\) sao cho \(MA + MB\) đạt giá trị nhỏ nhất. Khi đó \(a + b + c = - \frac{4}{3}\).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \[A\left( {1;1;0} \right),B\left( { - 1;0;1} \right),C\left( {1; - 2;3} \right)\].
a) Tứ giác \(ABCD\) là hình bình hành khi \(D\left( {3; - 1;2} \right)\).
b) Độ dài đoạn thẳng\(AB\) là \(\sqrt 6 \).
c) Biết \(E \in Oy,\) khi đó tam giác \(BCE\) vuông tại \(E\) thì \(E\left( {0; - 6;0} \right)\).
d) \[M\] là điểm nằm trên đoạn \[AB\] sao cho \[MA = 2MB\] thì độ dài \[OM\] bằng \[\frac{{\sqrt 6 }}{3}\].
PHẦN III. TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\), \(BC = a\sqrt 2 \), \[SA = a\sqrt 3 \] và \(SA\) vuông góc với đáy \(ABCD\). Gọi \[G\] là trọng tâm của tam giác \[ABD\]. Tính độ dài \[SG\].
Phần mái của một căn nhà có dạng là khối đa diện được mô tả và gắn trên hệ trục tọa độ \[Oxyz\] như hình vẽ. Tính thể tích khối đa diện của mái nhà.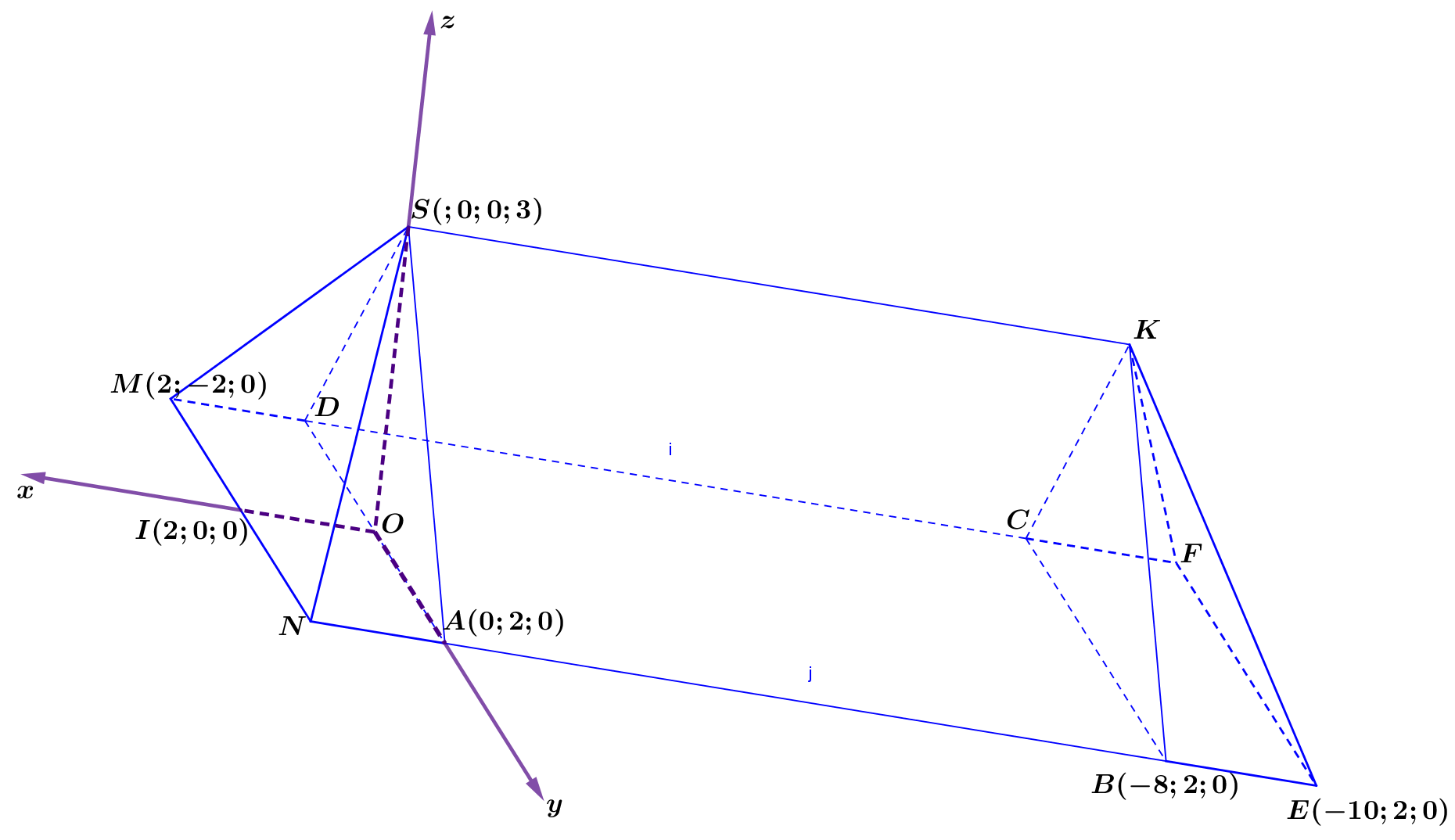
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\)có cạnh đáy bằng \(a\), \(CC' = a\sqrt 2 \). Góc giữa hai đường thẳng \(BA'\) và \(AC'\) là bao nhiêu?
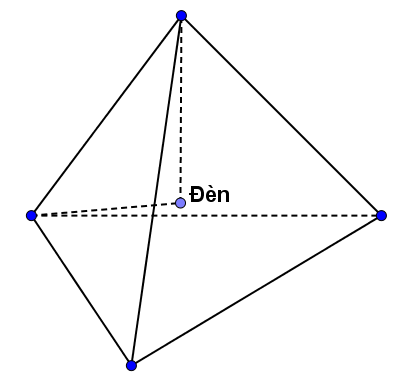
Một đồ chơi có dạng hình tứ diện đều làm bằng thủy tinh có cạnh bằng \(10cm\). Bên trong đặt một đèn nhỏ. Đèn đặt trên đường nối từ đỉnh của tứ diện xuống tâm của đường tròn ngoại tiếp đa giác đáy và cách đỉnh một khoảng là \(\frac{{5\sqrt 6 }}{2}cm\). Đèn được nối bởi hai dây qua hai đỉnh của tứ diện như hình vẽ. Cường độ lực tổng hợp của hai dây tác dụng lên đèn là bao nhiêu?
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1;0;0} \right)\),\(B\left( {0;1;0} \right)\) và \(C\left( {0;0;1} \right)\). Điểm \(M\)là điểm thỏa mãn \(P = M{A^2} + 2M{B^2} - M{C^2}\) đạt giá trị nhỏ nhất. Giá trị nhỏ nhất của \(P\) là ?
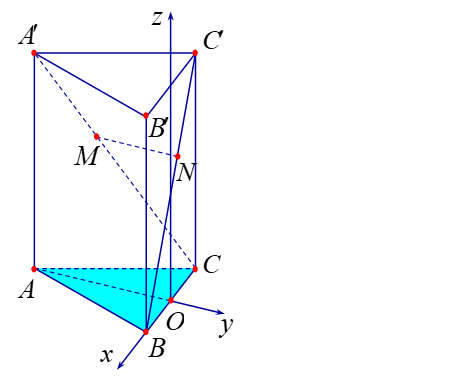
Một kiến trúc sư muốn xây dựng 1 tòa nhà biểu tượng độc lạ cho thành phố. Trên bản thiết kế tòa nhà có hình dạng là một khối lăng trụ tam giác đều, có cạnh bên bằng cạnh đáy và dài 300 mét (tham khảo hình vẽ) . Kiến trúc sư muốn xây dựng một cây cầu \(MN\) bắc xuyên tòa nhà (điểm đầu thuộc cạnh\(A'C\), điểm cuối thuộc cạnh \(BC'\)) và cây cầu này sẽ được dát vàng với đơn giá 5 tỷ đồng trên 1 mét dài. Vì vậy để đáp ứng bài toán kinh tế, kiến trúc sư phải chọn vị trí cây cầu sao cho \(MN\) ngắn nhất (Gợi ý: đoạn thẳng nối hai đường ngắn nhất chính là đường vuông góc chung). Khi đó giá xây cây cầu này hết bao nhiêu tiền?