20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 8. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong không gian Oxyz, cho \(\overrightarrow a = \left( {1;2;1} \right)\) và \(\overrightarrow b = \left( { - 1;3;0} \right)\). Vectơ \(\overrightarrow c = 2\overrightarrow a + \overrightarrow b \) có tọa độ là
(1; 7; 2).
(1; 5; 2).
(3; 7; 2).
(1; 7; 3).
Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = \left( {1;2;3} \right),\overrightarrow b = \left( {2;2; - 1} \right),\overrightarrow c = \left( {4;0; - 4} \right)\). Tọa độ của vectơ \(\overrightarrow d = \overrightarrow a - \overrightarrow b + 2\overrightarrow c \) là
(−7; 0; −4).
(−7; 0; 4).
(7; 0; −4).
(7; 0; 4).
Cho \(\overrightarrow a = \left( { - 1; - 1;2} \right),\overrightarrow b = \left( { - 1;1; - 1} \right),\overrightarrow c = \left( {2;4;7} \right)\). Tọa độ của vectơ \(\overrightarrow u = \overrightarrow a - 3\overrightarrow b + 2\overrightarrow c \) là
(0; 10; 13).
(6; −4; 19).
(6; 4; 19).
(−6; 4; 19).
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {3; - 4;1} \right)\) và \(\overrightarrow b = \left( {2; - 1;0} \right)\). Tích vô hướng \(\overrightarrow a .\overrightarrow b \) bằng
11.
10.
9.
8.
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;0; - 1} \right),\overrightarrow b = \left( {3; - 5;6} \right)\). Góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng
30°.
120°.
90°.
60°.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(2; 3; −1), N(−1; 1; 1), P(1; m – 1; 2). Tìm m để tam giác MNP vuông tại N.
m = 2.
m = −6.
m = 0.
m = −4.
Trong không gian Oxyz, cho hai điểm A(3; 1; −2), B(2; −3; 5). Điểm M thuộc đoạn AB sao cho MA = 2MB. Tọa độ điểm M là
\(\left( {\frac{7}{3}; - \frac{5}{3};\frac{8}{3}} \right)\).
(4; 5; −9).
\(\left( {\frac{3}{2}; - 5;\frac{{17}}{2}} \right)\).
(1; −7; 12).
Trong không gian Oxyz, cho tam giác ABC có A(1; 0; 1), B(0; 2; 3), C(2; 1; 0). Độ dài đường trung tuyến AM là
\(\frac{1}{2}\).
\(\frac{{\sqrt {11} }}{2}\).
\(\frac{{\sqrt {12} }}{2}\).
\(\frac{{\sqrt {10} }}{2}\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow {OM} = \left( {1;5;2} \right)\], \[\overrightarrow {ON} = \left( {3;7; - 4} \right)\], \(K\left( { - 1;3;1} \right)\). Gọi \[P\] là điểm đối xứng với \[M\] qua \[N\]. Tìm tọa độ vectơ \[\overrightarrow {KP} \].
\(\overrightarrow {KP} = \left( {6;6; - 11} \right)\).
\[\overrightarrow {KP} = \left( {8;6; - 11} \right)\].
\[\overrightarrow {KP} = \left( {6;6; - 4} \right)\].
\[\overrightarrow {KP} = \left( {3;3; - 2} \right)\].
Trong không gian \[Oxyz\] cho tam giác \[ABC\] có \[A\left( {1; - 1;1} \right),\,B\left( {5;0;2} \right),\,C\left( {0;4;3} \right)\]. Toạ độ trọng tâm \(G\)của tam giác \[ABC\] là
\(G\left( {3;\frac{5}{2};3} \right)\).
\(G\left( {2; - 1;2} \right)\).
\(G\left( {3; - \frac{5}{2};3} \right)\).
\(G\left( {2;1;2} \right)\).
Trong không gian Oxyz, cho tam giác ABC có các đỉnh A(1; −2; 0), B(2; 1; −2), C(0; 3; 4). Khi đó:
(a) Tọa độ của vectơ \(\overrightarrow {AB} \) là (1; 3; −2).
(b) Tọa độ trọng tâm của tam giác ABC là \(G\left( {1;\frac{2}{3};\frac{2}{3}} \right)\).
(c) Tọa độ hình chiếu của điểm B trên mặt phẳng Oxy là H(0; 0; −2).
(d)\(\overrightarrow x = 2\overrightarrow {AB} - 3\overrightarrow {BC} \). Tọa độ của vectơ \(\overrightarrow x = \left( { - 4;12;14} \right)\).
Trong không gian Oxyz, cho A(−5; 0; 7), B(1; 2; 1), C(16; 5; −2). Khi đó:
(a) \(\overrightarrow {AB} = \left( {6;2; - 6} \right)\).
(b) Góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) bằng 158,7°.
(c)\(\left| {\overrightarrow {BC} + \overrightarrow {AB} } \right| = 5\sqrt {22} \).
(d) Điểm N(a; b; c) thuộc đoạn AB thỏa mãn NA = 3NB. Khi đó a + b + c = 4,5.
Một căn phòng thiết kế hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA' = 3m, \(AD = 3\sqrt 3 \)m. Xét hệ trục tọa độ Oxyz, đỉnh A ≡ O, các điểm B, D, A' lần lượt nằm trên các trục Ox, Oy, Oz như hình vẽ
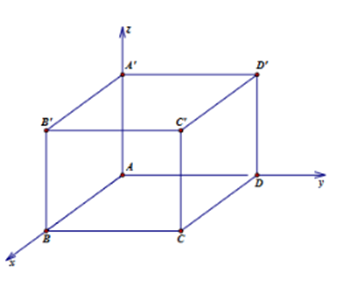
(a) Chiều cao của căn phòng là 3 m.
(b) Tọa độ của điểm B(3; 0; 0).
(c) \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} } \right| = 9\sqrt 2 \).
(d) Góc giữa hai vectơ \(\overrightarrow {A'C'} \) và \(\overrightarrow {DC} \) bằng 60°.
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;0; - 2} \right),\;B\left( { - 2;3;4} \right),\,C\left( {4; - 6;1} \right)\).
(a) Tọa độ trọng tâm G của tam giác là \(\left( {1; - 1;1} \right)\).
(b) \(\overrightarrow {AB} = \left( {3; - 3;6} \right),\,{\rm{ }}\overrightarrow {AC} = \left( { - 3;6; - 3} \right).\)
(c) Tam giác \(ABC\)là tam giác cân .
(d) Nếu \(ABDC\) là hình bình hành thì tọa độ điểm D là \(\left( {7; - 9; - 5} \right)\).
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1\;;\; - 2\;;\;7} \right);\;B\left( {5\;;6\;;\;3} \right);\;C\left( { - 4\;;\;7\;;\;10} \right)\).
(a)\(\overrightarrow {AB} = \left( {4\;;\;8\;;\; - 4} \right);\;\overrightarrow {AC} = \left( { - 5\;;\;9\;;\;3} \right);\;\overrightarrow {BC} = \left( { - 9\;;\;1\;;\;7} \right)\).
(b) Ba điểm A, B, C thẳng hàng.
(c) Chu vi tam giác ABC là \(4\sqrt 6 + \sqrt {115} + \sqrt {131} \).
(d) Diện tích tam giác \(ABC\)là \(S = \sqrt {590} \).
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm M(600; 400; 20) đến điểm N(800; 500; 30) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tốc độ của máy bay sau 15 phút tiếp theo là P(a; b; c). Tính a + b + c.
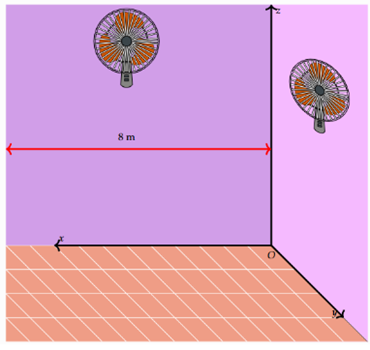
Trong một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có 1 cây quạt treo tường. Cây quạt A treo chính giữa bức tường và cách trần 1m, cây quạt B treo chính giữa bức tường và cách trần 1,5m. Chọn hệ trục tọa độ Oxyz như hình vẽ bên dưới (đơn vị mét). Giả sử \(\overrightarrow {AB} = \left( {a;b;c} \right)\). Tính a + b + c.

Trong không gian với hệ trục tọa độ \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có điểm \(B\) trùng với gốc tọa độ \(O\)và tọa độ các điểm \(A\left( {3;0;0} \right)\), \(D\left( {3;1;0} \right)\), \(B'\left( {0;0;5} \right)\). Gọi tọa độ \(C'\left( {m;n;p} \right)\). Tính \({m^2} + {n^2} + {p^2}\).
Trong không gian \(Oxyz\), cho điểm \(A\left( { - 3;0;0} \right)\), \(B\left( {0; - 4;0} \right)\). Gọi \(I\),\(J\) lần lượt là tâm đường tròn nội tiếp và ngoại tiếp của tam giác \(OAB\).Tính độ dài đoạn thẳng \(IJ\)(làm tròn kết quả đến hàng phần trăm).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\Delta ABC\] biết \[A\left( {2;0;0} \right)\], \[B\left( {0;2;0} \right)\], \[C\left( {1;1;3} \right)\]. \[H\left( {{x_0};{y_0};{z_0}} \right)\] là chân đường cao hạ từ đỉnh \[A\] xuống \[BC\]. Khi đó \[{x_0} + {y_0} + {z_0}\] bằng bao nhiêu? (làm tròn đến hàng phần trăm).








