Đề cương ôn tập giữa kì 1 Toán 7 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 2

Một nhà mạng cung cấp các gói mạng 4G theo tháng cho khách hàng. Trong đó, có hai gói phổ biến như sau:

− Gói cố định: Mức giá là \(285{\rm{ }}000\) đồng/tháng, không giới hạn data sử dụng.

− Gói linh hoạt: Mức giá là \(160{\rm{ 000}}\) đồng/tháng, cho phép khách hàng sử dụng 4Gb/ngày. Nếu vượt quá số data này, người dùng sẽ trả thêm \(5{\rm{ }}000\) đồng cho mỗi Gb vượt.

Giả sử mỗi tháng có 30 ngày, trung bình mỗi tháng anh Hải sử dụng 150Gb. Hỏi anh Hải nên đăng kí theo hình thức nào tiết kiệm hơn? Và tiết kiệm được bao nhiêu tiền mỗi tháng?

Một hộp sữa có dạng hình hộp chữ nhật với các kích thước của đáy dưới là 5 cm và \[4{\rm{ cm;}}\] chiều cao là 8 cm. Khi đó, diện tích xung quanh của hộp sữa là bao nhiêu?

Một cái bể cá có chiều dài 2 m; chiều rộng 80 cm và chiều cao 80 cm. Người ta cần đổ vào bể cá bao nhiêu m³ nước thì đầy bể?

Cho hình lập phương có diện tích một mặt là \[144{\rm{ }}{{\rm{m}}^{\rm{2}}}{\rm{.}}\] Tính thể tích của hình lập phương đó.

Hình lăng trụ đứng có đáy là một hình bình hành với cạnh đáy là 6 cm và chiều cao tương ứng với cạnh đáy là 8 cm. Chiều cao của hình lăng trụ đứng là 12 cm. Tính thể tích hình lăng trụ.

Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6 m; chiều rộng 4,5 m và chiều cao 4 m. Chủ nhà dự định ốp gỗ mặt nền và một phần tường với độ cao gỗ ốp lên tường là 1,5 m. Chi phí mỗi mét vuông là 600 000 đồng (kể cả công và gỗ ốp). Hỏi để ốp gỗ căn phòng như dự định, chủ nhà cần thanh toán bao nhiêu tiền?

Một nhóm học sinh cần chuẩn bị lều để đi cắm trại. Nhóm dự tính dựng lều trại hình lăng trụ đứng tam giác với kích thức như hình vẽ. Lều được phủ kín bằng vải bạt (tính cả mặt tiếp xúc với mặt đất) có giá 150 000 đồng \[{\rm{/}}\,{{\rm{m}}^{\rm{2}}}{\rm{.}}\] Số tiền tối đa chi cho mua vải là \[6\,\,000\,\,000\] đồng. Hỏi nhóm học sinh có đủ tiền mua vải không?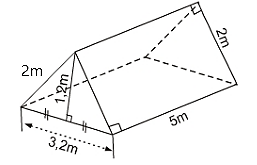

Cho hình lăng trụ đứng tứ giác với các kích thước như hình vẽ bên. Tính thể tích của hình lăng trục đứng.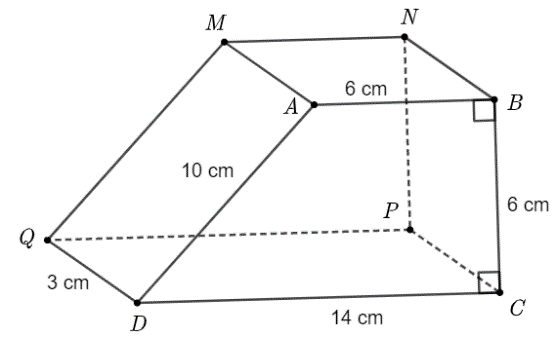

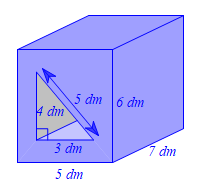
a) Cho hình lăng trụ đứng có đáy là tam giác vuông có hai cạnh góc vuông là \({\rm{3}}\,\,{\rm{cm}}\) và \({\rm{4}}\,\,{\rm{cm}}\), cạnh huyền là \({\rm{5}}\,\,{\rm{cm}}\). Tính diện tích tất cả các mặt và thể tích của hình lăng trụ đứng đó biết lăng trụ đứng có chiều cao là \({\rm{6}}\,\,{\rm{cm}}\).

ii) Người ta cần sơn toàn bộ các mặt của khối gỗ, tính diện tích bề mặt cần sơn.

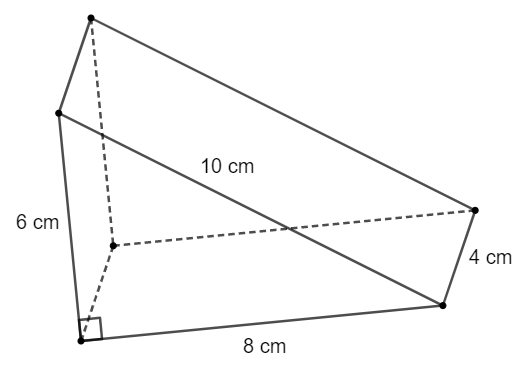
Một cái bánh ngọt có dạng hình lăng trụ đứng tam giác có kích thước như hình vẽ. Người ta làm một chiếc hộp bằng bìa cứng để cái bánh này thì diện tích bìa cứng cần dùng là bao nhiêu? (Coi các mép dán không đáng kể).

Cho hình vẽ bên.

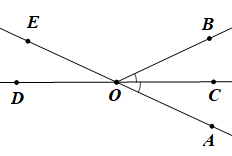
Biết \(\widehat {AOB} = 50^\circ \), tia \(OC\) là tia phân giác của góc \(AOB\).

a) Vẽ lại hình và kể tên góc kề bù với góc \(AOC.\)

b) Tính số đo của mỗi góc \(BOE,\,\,AOD\).

Cho hình vẽ bên.

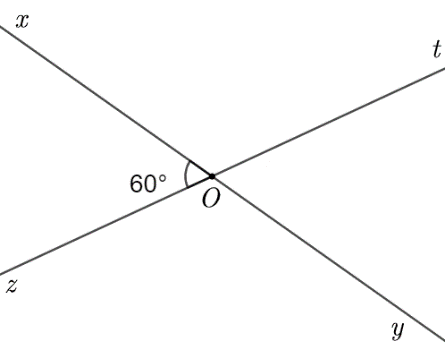
a) Kể tên các cặp góc đối đỉnh trong hình.

b) Vẽ \(Om\) là tia phân giác của góc \(\widehat {xOz}\). Tính số đo góc \[\widehat {tOy};\,\,\widehat {xOt};\]\(\widehat {mOx}\).

Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 80^\circ \). Trên mặt phẳng bờ \(Ox\) chứa tia \(Oz\) vẽ tia \(Ot\) sao cho \[\widehat {xOt} = 160^\circ \]. Chứng tỏ \(Oz\) là tia phân giác của \(\widehat {xOt}\).

Cho hình vẽ bên. Biết \(\widehat {xOz} = 97^\circ ,\,\,\widehat {tOu} = 82^\circ \) và tia \(Oz\) là tia phân giác của góc \(\widehat {tOu}\).

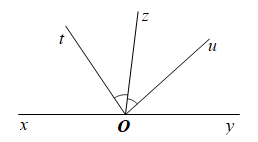
a) Vẽ lại hình và kể tên các cặp góc kề bù (không tính góc bẹt) có trong hình vẽ.

b) Tính số đo của góc \(\widehat {tOz},\,\,\widehat {tOy}\).

Cho góc bẹt \(xOy\). Vẽ ba tia \(Om,\,\,On,\,\,Oz\) sao cho tia \(Om\) nằm giữa hai tia \[Ox,\,\,Oz\] và \(\widehat {xOm} = 50^\circ ,\,\,\widehat {xOz} = 130^\circ \). Vẽ tia \(On\) là tia đối của tia \(Oz.\)

a) Vẽ hình và kể tên các góc kề bù với góc \(xOz\) có trong hình vẽ.

b) Tính số đo của góc \(yOz.\) Giải thích tại sao tia \[Ox\] là tia phân giác của góc \(mOn.\)

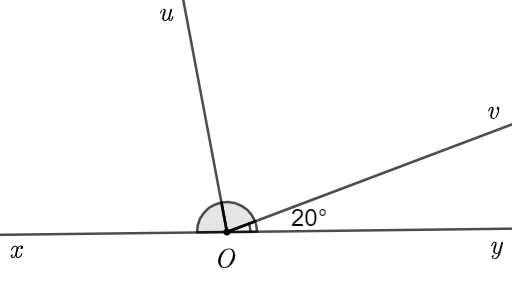
Cho hình vẽ sau. Biết \(\widehat {xOy}\) là góc bẹt và \(Ou\) là tia phân giác của \(\widehat {xOv}\). Tính số đo \(\widehat {uOv}\).

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

a) \(\frac{5}{{n - 2}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:b) \(\frac{{ - 6}}{{n + 1}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

c) \(\frac{{ - 3}}{{n - 4}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:d) \(\frac{{6n - 4}}{{2n + 1}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:e) \(\frac{{3n + 2}}{{4n - 5}}\);

Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:

g) \(\frac{{4n - 1}}{{3 - 2n}}\).

Tìm giá trị nhỏ nhất của biểu thức:

a) \[{\left( {2x - 3} \right)^2} + 15\];

Tìm giá trị nhỏ nhất của biểu thức:

b) \({\left( {5x + 7} \right)^8} - 2020\);

Tìm giá trị nhỏ nhất của biểu thức:

c) \(2016 + \left| {1 - 2019x} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:d) \( - 9 + \left| {4x + 1} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:e) \(\left| {x - 1} \right| + \left| {x - 2} \right|\);

Tìm giá trị nhỏ nhất của biểu thức:

g) \(2021 - \frac{{15}}{{3 + \left| {x - 2021} \right|}}\).

Tìm giá trị lớn nhất của biểu thức:

a) \[8 - {\left( {4x - 7} \right)^2}\];        

Tìm giá trị lớn nhất của biểu thức:b) \(7 - \left| {6x - 1} \right|\);

Tìm giá trị lớn nhất của biểu thức:

c) \(6 - \left| {{x^2} + 5} \right|\);

Tìm giá trị lớn nhất của biểu thức:d) \(14 + \frac{3}{{2 + {{\left( {5x - 6} \right)}^2}}}\);

Tìm giá trị lớn nhất của biểu thức:e) \( - 6 + \frac{{15}}{{5 + \left| {7x + 4} \right|}}\);   

Tìm giá trị lớn nhất của biểu thức:

g) \(\frac{{4{x^2} + 9}}{{{x^2} + 1}}\).

Tìm giá trị nhỏ nhất của biểu thức \[P = \frac{{14 - x}}{{4 - x}}\] với mọi .\(x \in \mathbb{Z}\).. Khi đó \[x\] nhận giá trị nguyên nào?

Tính giá trị biểu thức \(A = \frac{{2x + 3y}}{{x + 2y}}\) biết \(\frac{x}{y} = \frac{1}{2}\).

Tìm giá trị nhỏ nhất của biểu thức \(A = {\left( {{x^2} - 9} \right)^2} + \left| {y - 2} \right| + 10\).