Đề cương ôn tập cuối kì 1 Toán 7 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 3

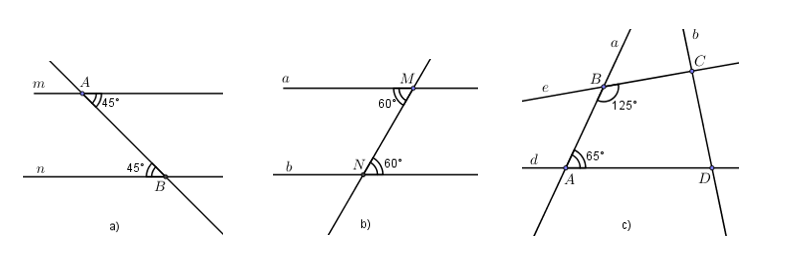
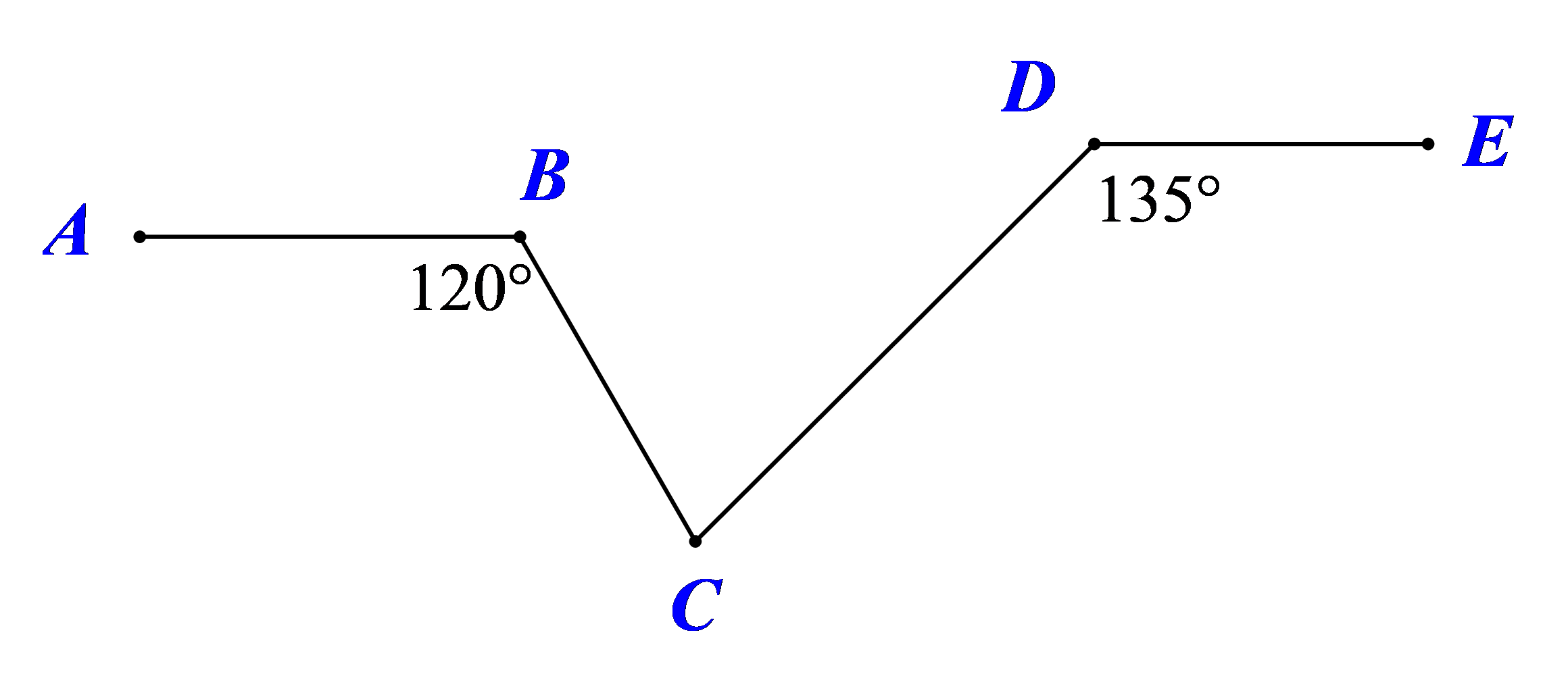
Cho hình vẽ \(AB\,{\rm{//}}\,DE\). Tính số đo \(\widehat {BCD}\).

Cho hình vẽ sau.

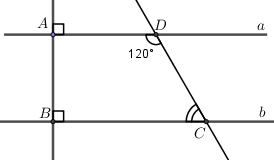
a) Chứng minh \(a\parallel b\).

b) Tính số đo góc \(C\).

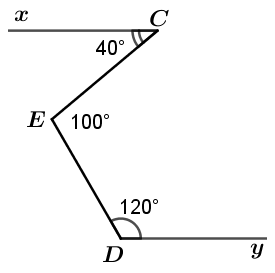
Cho hình vẽ bên, biết \(\widehat C = 40^\circ ,\widehat D = 120^\circ ,\widehat E = 100^\circ \). Chứng tỏ \(Cx\parallel Dy\).

Cho hình vẽ bên biết thanh gỗ \(AB\)dựa vào tường làm thành góc \(63^\circ \) so với mặt đất, người ta dùng tiếp thanh gỗ \(CD\) đặt vuông góc với tường sao cho điểm \(D\)nằm trên thanh gỗ \(AB\). Hãytính góc tạo bởi thanh gỗ \(CD\) và thanh gỗ \(AB\).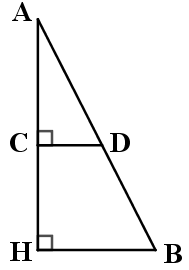

Cho hình vẽ dưới đây biết \(\widehat {DCn} = 70^\circ \).

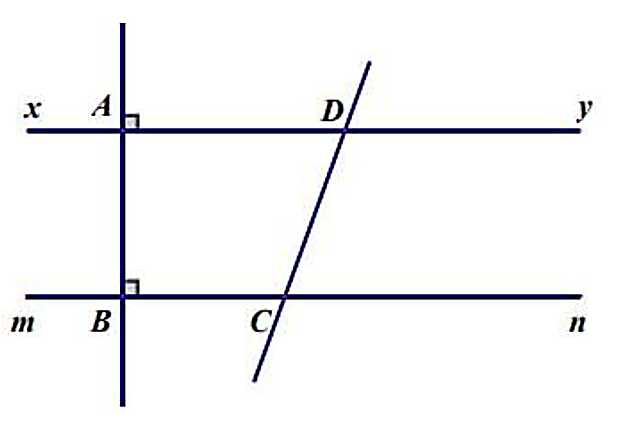
a) Chứng minh \(xy\parallel mn.\)

b) Tính số đo góc \(\widehat {DCy}\).

c) Kẻ tia phân giác của \(\widehat {DCy}\) cắt đường thẳng \(mn\) tại \(E\). Tính số đo góc \(\widehat {ADE}\).

Cho hình vẽ bên. Biết \(My\parallel Pt\), \(\widehat {xMy} = 60^\circ \), \(\widehat {MNz} = 60^\circ \).

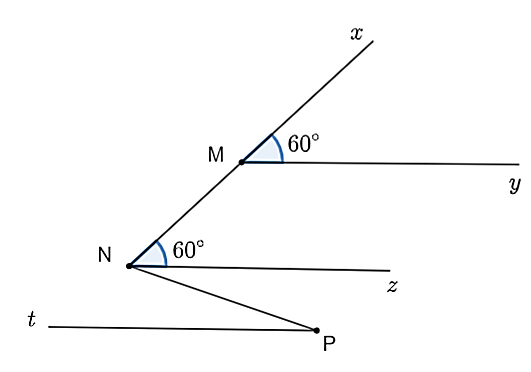
a) Chứng minh \(My\parallel Nz.\)

b) Chứng minh \(Nz\parallel Pt.\)

c) Biết \(\widehat {xNP} = 85^\circ \), tính số đo góc \(\widehat {NPt}\).

Cho hình vẽ bên, biết rằng \(\widehat {BAy} = 120^\circ \), \(\widehat {tCx} = 30^\circ ,\)\(\widehat {tBA} = 90^\circ \). Bạn Nam cho rằng: đường thẳng \(Cx\) và \(Ay\) song song với nhau. Theo em, bạn Nam nói đúng hay sai? Vì sao?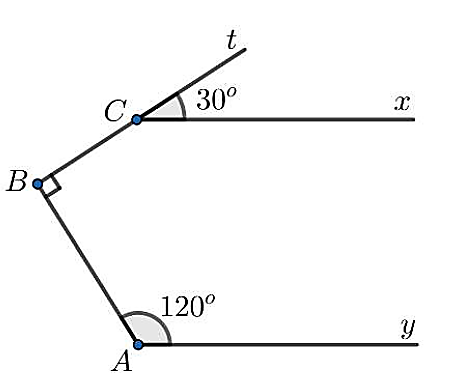

Cho hình vẽ bên, biết \(a \bot CD\), \(b \bot CD\) và \(\widehat {{B_3}} = 45^\circ \).

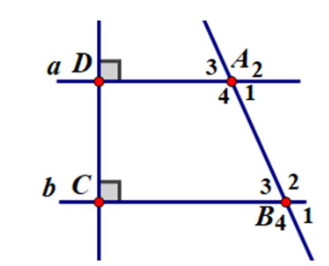
a) Chứng minh rằng \(a\parallel b.\)

b) Tính \(\widehat {{A_1}},\,\,\widehat {{A_2}}.\)

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:

a) \(A = 1,25 + \left| {2,5 - x} \right|\).         

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:

b) \(B = - 2{\left( {x - 3} \right)^2} - \frac{7}{{11}}\left| {3y + 7} \right| - 2011\).

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:c) \(C = {\left( {2x + \frac{1}{3}} \right)^2} - 1\).                     

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:

d) \(D = \left| {2x - 1} \right| + \left| {2x - 5} \right|\).

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:e) \(E = \frac{3}{{{{\left( {2x - 3} \right)}^{2024}} + 5}}\)

Tính giá trị lớn nhất, giá trị nhỏ nhất của các biểu thức sau:

f) \(F = \frac{5}{{{{\left( {{x^2} + 3} \right)}^2} - 1}}\).

Tìm \(x \in \mathbb{Z}\) để các biểu thức sau có giá trị nguyên.

a) \(A = \frac{5}{{2x - 3}}\);

Tìm \(x \in \mathbb{Z}\) để các biểu thức sau có giá trị nguyên.b) \(B = \frac{{2x - 1}}{{x + 1}}\);     

Tìm \(x \in \mathbb{Z}\) để các biểu thức sau có giá trị nguyên.c) \(C = \frac{5}{{{x^2} - 3}}\);

Tìm \(x \in \mathbb{Z}\) để các biểu thức sau có giá trị nguyên.

d) \(D = \frac{{\sqrt x - 3}}{{\sqrt x + 2}}\).

Tìm \[x\]:

a) \[\frac{{x + 1}}{{99}} + \frac{{x + 2}}{{98}} + \frac{{x + 3}}{{97}} + \frac{{x + 4}}{{96}} = - 4\];

Tìm \[x\]:

b) \[\frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{x\left( {x + 1} \right)}} = \frac{{2008}}{{2009}}\];

Tìm \[x\]

c) \[\frac{{x - 214}}{{86}} + \frac{{x - 132}}{{84}} + \frac{{x - 54}}{{82}} = 6\];

Tìm \[x\] biết:

d) \[\left| {x + \frac{1}{{1.2.3}}} \right| + \left| {x + \frac{1}{{2.3.4}}} \right| + \left| {x + \frac{1}{{3.4.5}}} \right| + .... + \left| {x + \frac{1}{{18.19.20}}} \right| = 19x\];

Tìm \[x\] biết:

e) \(\left| {x + \frac{{19}}{5}} \right| + \left| {y + \frac{{1890}}{{1975}}} \right| + \left| {z - 2004} \right| = 0\);

Tìm \[x\]

f) \(\left| {x + \frac{9}{2}} \right| + \left| {y + \frac{4}{3}} \right| + \left| {z + \frac{7}{2}} \right| \le 0\);

Tìm \[x\]

g) \(\left| {x - 1,5} \right| + \left| {2,5 - x} \right| = 1\);

Cho \[{\left( {{a_1}m - {b_1}n} \right)^{2024}} + {\left( {{a_2}m - {b_2}n} \right)^{2024}} + {\left( {{a_3}m - {b_3}n} \right)^{2024}} + ... + {\left( {{a_{2025}}m - {b_{2025}}n} \right)^{2024}} \le 0\].

Chứng minh rằng: \[\frac{{{a_1} + {a_2} + {a_3} + ... + {a_{2025}}}}{{{b_1} + {b_2} + {b_3} + ... + {b_{2025}}}} = \frac{n}{m}\].

Cho \(\frac{{nz - py}}{m} = \frac{{px - mz}}{n} = \frac{{my - nx}}{p}\). Chứng minh rằng: \(m\), \(n\), \(p\) lần lượt tỉ lệ với \(x\), \(y\), \(z\)

(giả sử các tỉ số đều có nghĩa).

Cho \(a\), \(b\), \(c\) là ba số khác 0 thỏa mãn: \(\frac{{ab}}{{a + b}} = \frac{{bc}}{{b + c}} = \frac{{ca}}{{c + a}}\) (với giả thiết các tỉ số đều có nghĩa). Tính giá trị của biểu thức \(M = \frac{{ab + bc + ca}}{{{a^2} + {b^2} + {c^2}}}\).

Cho 4 số thực \(a\), \(b\), \(c\), \(d\) khác 0 thỏa mãn \(a + b + c + d \ne 0\) và

\(\frac{{2a + b + c + d}}{c} = \frac{{a + 2b + c + d}}{b} = \frac{{a + b + 2c + d}}{c} = \frac{{a + b + c + 2d}}{d}\).

Tìm giá trị của biểu thức \(M\), biết \(M = \frac{{a + b}}{{c + d}} + \frac{{b + c}}{{d + a}} + \frac{{c + d}}{{a + b}} + \frac{{d + a}}{{b + c}}\).

Cho \[a,\,\,b,\,\,c\] là ba số thực khác 0 thỏa mãn điều kiện \(\frac{{a + b - c}}{c} = \frac{{b + c - a}}{a} = \frac{{c + a - b}}{b}.\)Tính giá trị biểu thức \[B = \left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{c}{b}} \right)\].

Cho \(\frac{{{x^2} - yz}}{a} = \frac{{{y^2} - zx}}{b} = \frac{{{z^2} - xy}}{c}\). Chứng minh rằng \(\frac{{{a^2} - bc}}{x} = \frac{{{b^2} - ca}}{y} = \frac{{{c^2} - ab}}{z}\).

Hai xe ô tô khởi hành cùng một lúc từ hai địa điểm \(A\) và \(B\), đi ngược chiều nhau trên cùng một tuyến đường. Đến điểm gặp nhau, xe thứ hai đi được quãng đường dài hơn xe thứ nhất là \(20{\rm{ km}}{\rm{.}}\) Biết rằng nếu đi hết quãng đường \(AB,\) xe thứ nhất đi hết 4 giờ 15 phút, xe thứ hai đi hết 3 giờ 45 phút. Tính độ dài quãng đường \(AB\).

Gạo được chứa trong ba kho theo tỉ lệ \(1,3;{\rm{ 2}}\frac{1}{2};{\rm{ 1}}\frac{1}{5}\). Gạo trong kho thứ hai nhiều hơn trong kho thứ nhất là \(43,2\) tấn. Sau 1 tháng, người ta tiêu thụ ở kho thứ nhất \(40\% \) và ở kho thứ hai \(30\% \) và ở kho thứ ba là 25% số gạo có trong mỗi kho. Hỏi trong một tháng đã tiêu thụ được bao nhiêu tấn gạo?

Nhà trường dự định chia vở cho ba lớp 7A, 7B, 7C theo tỉ lệ \(7;6;5\). Nhưng vì có sự thay đổi nên phải chia lại theo tỉ lệ \(6;5;4\). Như vậy có lớp đã nhận được ít hơn dự định 12 quyển. Tính số vở mỗi lớp đã nhận được trong thực tế.

Trên một công trường xây dựng, do cải tiến kỹ thuật nên năng suất lao động của công nhân tăng \(25\% \). Hỏi nếu số công nhân không thay đổi thì thời gian làm xong việc giảm bao nhiêu phần trăm?

Ông Hậu khoán số tiền \[3,6\] triệu đồng để thuê sơn tường nhà ông cho một nhóm thợ. Sau khi người thứ nhất làm được 7 giờ và người thứ hai làm 4 giờ thì họ làm được \[\frac{5}{9}\] công việc. Sau đó họ cùng làm trong 4 giờ thì chỉ còn \[\frac{1}{{18}}\] bức tường chưa sơn. Vì hai người này bận công việc khác nên đưa người thứ ba làm phần còn lại. Xong việc ông Hậu trả tiền, nhưng cả ba lúng túng không biết phân chia như thế nào. Ông Hậu nói phải chia theo phần công việc mỗi người đã làm chứ không theo giờ làm được vì năng suất mỗi người không như nhau. Em hay giúp ông Hậu tính toán tiền công của mỗi người.

Ban tổ chức có 40 phần quà đem phát cho 13 đội. Có \[x\] đội vì công việc nên phải rời đi sớm, mỗi đội nhận được 3 phần quà và không tham gia vào lần phát quà. Phần quà còn lại được chia đều cho các đội còn lại. Hỏi mỗi đội còn lại nhận được nhiều nhất bao nhiêu phần quà?

Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng \(96{\rm{ d}}{{\rm{m}}^2}\). Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết \(3,2{\rm{ }}{{\rm{m}}^2}\) tôn (diện tích các mép hàn không đáng kể).

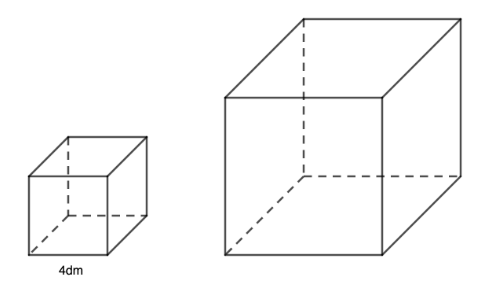
Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?