Đề cương ôn tập cuối kì 1 Toán 7 Cánh diều cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án
30 câu hỏi
Cho hình vẽ dưới đây, biết rằng \(Ax\parallel yy'\), \(\widehat {xAB} = 40^\circ ,{\rm{ }}\widehat {CBA} = 65^\circ ,{\rm{ }}\widehat {BCy} = 65^\circ \). Kẻ \(BD\) là tia phân giác của \(\widehat {CBy}\).
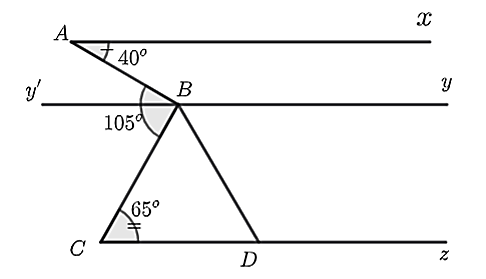
a) \(\widehat {ABy'}\) và \(\widehat {y'BC}\) là hai góc kề nhau.
b) \(\widehat {xAB} = \widehat {BAy'} = 40^\circ \).
c) \(yy'\parallel Cx.\)
d) \(\widehat {CDB} > 60^\circ \).
Cho hình vẽ sau, biết \[xy\parallel pq\], \[\widehat {DCB} = 90^\circ ,\widehat {ABq} = 60^\circ \].
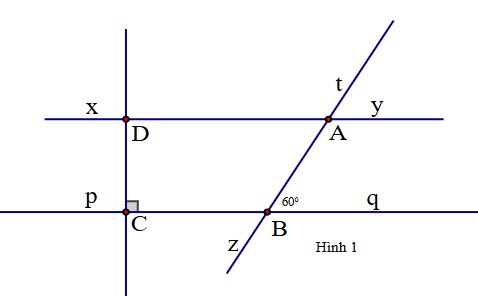
Xét tính đúng sai của các khẳng định dưới đây.
a) \[\widehat {xDC}\] và \[\widehat {DCB}\] là hai góc đồng vị.
b) \[\widehat {zBC}\] và \[\widehat {yAt}\] là hai góc đồng vị.
c) Hai đường thẳng \[xy\] và \[CD\] vuông góc với nhau.
d) \[\widehat {BAy}\] và \[\widehat {qBA}\] là hai góc bù nhau.
Tổng kết các phong trào thi đua chào mừng ngày Nhà Giáo Việt Nam 20/11, ba lớp 7A, 7B, 7C được thưởng 160 quyển vở. Biết số vở ba lớp 7A, 7B, 7C lần lượt tỉ lệ với 9; 7; 4. Gọi \[x,y,z\] lần lượt là số quyển vở được thưởng của ba lớp 7A, 7B, 7C.
a) \[x + y + z = 160\].
b) Số vở ba lớp 7A, 7B, 7C được thưởng tỉ lệ với 9; 7; 4 nên \[9x = 7y = 4z\].
c) Lớp 7A được thưởng số quyển vở nhiều nhất.
d) Có hai lớp được thưởng số vở nhiều hơn 60 quyển.
Một công trường xây dựng cần chuyển \[35,7\] tấn sắt. Lần đầu chở được \[\frac{4}{7}\] số sắt đó về bằng xe tải, mỗi xe tải chở được \[1,7\] tấn sắt, lần thứ hai chở hết số sắt còn lại với số xe tải bằng \[\frac{1}{2}\] số xe lúc ban đầu.
a) Số tấn sắt lần đầu chở được \[20,4\] tấn.
b) Số tấn sắt chở lần hai nhiều hơn 15 tấn.
c) Tổng số xe tải sử dụng trong hai lần là 18 xe.
d) Mỗi xe lúc sau chở ít hơn 2,5 tấn sắt.
Ba đội công nhân làm ba khối lượng công việc như nhau. Đội công nhân thứ nhất, thứ hai, thứ ba hoàn thành công việc với thời gian là 8 ngày; 10 ngày và 12 ngày. Biết rằng đội thứ ba kém đội thứ nhất 5 công nhân và năng suất lao động của mỗi người là như nhau. Gọi số công nhân trong đội thứ nhất, thứ hai và thứ ba lần lượt là \[x,y,z\] (người) \[\left( {x,y,z \in {\mathbb{N}^*}} \right)\].
a) Vì khối lượng công việc như nhau nên số người tỉ lệ nghịch với thời gian.
b) \[8x = 10y = 12z\] và \[z - x = 15\].
c) Đội thứ ba có ít số công nhân nhất.
d) Tổng số công nhân của cả ba đội là 37 công nhân.
Nhà ông An thuê thợ làm một cái gờ bằng bê tông để xe máy lên xuống bậc thêm có hình dạng giống như hình lăng trụ đứng tam giác dưới đây.
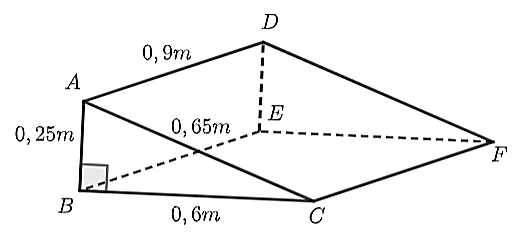
Biết rằng \(AB = 0,25{\rm{ m; }}BC = 0,6{\rm{ m; }}AC{\rm{ = 0,65 m; }}AD = 0,9{\rm{ m}}\). Cho biết, tiền quét vôi các mặt xung quanh (trừ hai mặt đáy) của gờ là \(300{\rm{ 000}}\) đồng và tiền đổ bê tông là \(1{\rm{ d}}{{\rm{m}}^3}\) giá \(50{\rm{ 000}}\) đồng.
a) Diện tích được quét vôi của cái gờ là \(1,35\) m2.
b) Thể tích của gờ lớn hơn \(0,05{\rm{ }}{{\rm{m}}^3}.\)
c) Số tiền mua bê tông làm chiếc gờ này nhỏ hơn \(3,3\) triệu đồng.
d) Tổng số tiền ông An phải trả là \(3,5\) triệu đồng.
Căn phòng của bác An có một cửa lớn hình chữ nhật và một cửa sổ hình vuông với kích thước như hình bên. Bác cần sơn các bức tường xung quanh và trần của căn phòng này (không sơn cửa). Biết rằng, để sơn mỗi mét vuông cần phải tốn \(250{\rm{ }}000\) đồng.
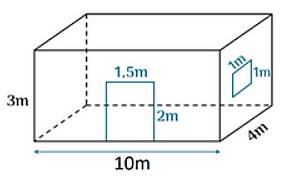
a) Tổng diện tích các cửa của căn phòng này là \(4{\rm{ }}{{\rm{m}}^2}\).
b) Diện tích xung quanh của căn phòng là \(84{\rm{ }}{{\rm{m}}^2}.\)
c) Tổng diện tích cần sơn bằng \(80{\rm{ }}{{\rm{m}}^2}.\)
d) Chi phí đề bác An sơn căn phòng đó lớn hơn \(20\) triệu đồng.
Giá niêm yết của một thùng sữa milo là \[320{\rm{ }}000\] đồng. Nhân ngày 1/6 cửa hàng giảm giá \[5\% \] và giảm thêm \[2\% \] cho khách hàng thứ 300 của cửa hàng.
a) Vị khách thứ 300 được giảm \[7\% \].
b) Số tiền mà vị khách thứ 300 phải thanh toán nhỏ hơn 300 nghìn đồng.
c) Vị khách thứ 301 phải trả 304 nghìn đồng khi mua thùng sữa.
d) Vị khách thứ 300 tiết kiệm được 4000 đồng so với các khách hàng mua sữa khác.
Hai vòi cùng chảy vào một bể. Nếu vòi thứ nhất chảy thì mất 4 giờ 25 phút mới đầy bể. Vòi thứ hai chảy thì mất 8 giờ mới đầy bể.
a) Trong một giờ, vòi thứ nhất chảy đuược \[\frac{{13}}{{53}}\] bể nước.
b) Trong một giờ, vòi thứ hai chảy được nhiều hơn vòi thứ nhất.
c) Trong một giờ, cả hai vòi cùng chảy được một lượng nhỏ hơn \[\frac{1}{2}\] bể.
d) Các hai vòi cùng chảy vào bể thì sau 12 giờ đầy bể.
Bình đọc một quyển sách trong 4 ngày. Ngày thứ nhất đọc được \[\frac{1}{5}\] quyển sách, ngày thứ hai đọc được \[\frac{1}{3}\] quyển sách, ngày thứ ba đọc được \[\frac{1}{4}\] quyển sách.
a) Ngày thứ tư, bạn Bình đọc được \[\frac{{13}}{{60}}\] quyển sách.
b) Hai ngày đầu, bạn Bình đọc được \[\frac{4}{{15}}\] quyển sách.
c) Hai ngày sau, bạn Bình đọc được \[\frac{8}{{15}}\] quyển sách.
d) Hai ngày đầu Bình đọc được nhiều hơn hai ngày sau.
Một chiếc ti vi có đường chéo dài \[48{\rm{ inch}}\], hãy tính độ dài đường chéo của ti vi này theo đơn vị cm với độ chính xác \[d = 0,05\] (cho biết \[1{\rm{ inch}} \approx 2,54{\rm{ cm}}\]).
Biết độ dài ba cạnh của tam giác tỉ lệ với 5; 6; 7 và chu vi tam giác bằng 36. Hỏi độ dài lớn nhất của tam giác đó bằng bao nhiêu?
Bố của Phúc chuẩn bị đi công tác bằng máy bay. Theo kế hoạch, máy bay sẽ cất cánh lúc 10 giờ 30 phút. Bố của Phúc cần phải có mặt ở sân bay trước ít nhất 2 giờ để làm thủ tục, biết rằng đi từ nhà Phúc đến sân bay mất khoảng 45 phút. Hỏi bố của Phúc phải đi từ nhà muộn nhất là lúc mấy giờ đến đến sân bay cho kịp giờ bay? (Kết quả viết dưới dạng số thập phân)
Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \].
![Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \]. Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/21-1758544877.png)
Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ?
Cho hình vẽ dưới đây:
![Cho hình vẽ dưới đây: Hỏi số đo góc bù với góc \[\widehat {xOy}\] trong hình trên là bao nhiêu lần độ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/23-1758544921.png)
Hỏi số đo góc bù với góc \[\widehat {xOy}\] trong hình trên là bao nhiêu lần độ?
Cho hình vẽ, biết \[\widehat {mAB} = 60^\circ ,\]\[\widehat {DBe} = 75^\circ \]; \[\widehat {ACD} = 60^\circ \].
![Cho hình vẽ, biết \[\widehat {mAB} = 60^\circ ,\]\[\widehat {DBe} = 75^\circ \]; \[\widehat {ACD} = 60^\circ \]. Hỏi số đo \[\widehat {CDt}\] bằng bao nhiêu độ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/24-1758544948.png)
Hỏi số đo \[\widehat {CDt}\] bằng bao nhiêu độ?
Hai đoạn ống nước có chiều dài lần lượt là \(0,8{\rm{ m}}\) và \(1,35{\rm{ m}}\). Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là \(\frac{2}{{25}}{\rm{ m}}{\rm{.}}\) Hỏi đoạn ống nước mới dài bao nhiêu mét? (Kết quả viết dưới dạng số thập phân)
Nhân dịp khai trương, cửa hàng thời trang bán giảm giá tất cả các mặt hàng \(20\% \). Bạn Hạnh dự định mua 2 cái áo giá 200 nghìn đồng/cái và 3 cái quần giá 300 nghìn đồng/cái. Hỏi bạn Hạnh phải trả cho cửa hàng bao nhiêu tiền? (Đơn vị: nghìn đồng)
Tìm giá trị của \[x\] thỏa mãn: \[x:2\frac{1}{4} - 3\frac{1}{2} = - \frac{1}{2}\]. (Kết quả ghi dưới dạng số thập phân)
Tìm giá trị \[x > 1\] thỏa mãn: \[\frac{8}{5} - \left| {\frac{3}{4} - x} \right| = {2024^0}\]. (Kết quả ghi dưới dạng số thập phân)
Thực hiện phép tính
a) \(\frac{1}{9} - 0,3 \cdot \frac{5}{9} + \frac{1}{3} + 5\) ;
Thực hiện phép tính
b) \(\left( {1 + \frac{2}{3} - \frac{1}{4}} \right){\left( {0,8 - \frac{3}{4}} \right)^2}\);
Thực hiện phép tínhc) \(\left( {{2^2}:\frac{4}{3} - \frac{1}{2}} \right) \cdot \frac{6}{5} - 17\);
Thực hiện phép tính
d) \({\left( {\frac{1}{3}} \right)^{50}} \cdot {\left( { - 9} \right)^{25}} - \frac{2}{3}:4\);
Thực hiện phép tínhe) \(\left| {\frac{{ - 1}}{2}} \right| + {\left( {\frac{{ - 1}}{3}} \right)^2}:\left| { - 2} \right| - {\left( {\frac{{ - 2}}{3}} \right)^0}\) ;
Thực hiện phép tính
f) \(\frac{{\sqrt {{3^2}} + \sqrt {{{39}^2}} }}{{\sqrt {{{91}^2}} - \sqrt {{{( - 7)}^2}} }}\);
Thực hiện phép tínhg)\(10\,.\,\sqrt {0,01} \, \cdot \,\sqrt {\frac{{16}}{9}} + 3\sqrt {49} - \frac{1}{6}\, \cdot \,\sqrt 4 \) ;
Thực hiện phép tính
h) \(0,8:\left\{ {0,2 - 7\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\) ;
Thực hiện phép tínhi) \(\frac{3}{5}:\left( {\frac{{ - 1}}{{15}} - \frac{1}{6}} \right) + \frac{3}{5}:\left( {\frac{{ - 1}}{3} - 1\frac{1}{{15}}} \right)\);
Thực hiện phép tính
k) \({\left( {\frac{3}{5}} \right)^{10}}.{\left( {\frac{5}{3}} \right)^{10}} - \frac{{{{13}^4}}}{{{{39}^4}}} + {2014^0}\).








