Đề cương ôn tập giữa kì 1 Toán 7 Cánh diều cấu trúc mới (Trắc nghiệm) có đáp án
36 câu hỏi
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với
\[a,\,\,b \in \mathbb{N};\,\,a \ne 0\].
\[a,\,\,b \in \mathbb{N};\,\,b \ne 0\].
\[a,\,\,b \in \mathbb{Z};\,\,b \ne 0\].
\[a = 0;\,\,b \ne 0\].
Trong các số sau đây, số nào biểu diễn số hữu tỉ \(\frac{{ - 2}}{3}\)?
\(\frac{4}{6}\).
\(\frac{{ - 6}}{9}\).
\(\frac{{ - 4}}{9}\).
\(\frac{{ - 4}}{{ - 6}}\).
Đối với biểu thức có chứa dấu ngoặc thì thứ tự thực hiện phép tính trên tập số hữu tỉ nào dưới đây là đúng?
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\).
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\).
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\).
\(\left( {} \right) \to \left\{ {} \right\} \to \left[ {} \right]\).
Cho trục số.

Điểm \(B\) trên trục số biểu diễn số hữu tỉ nào?
\(\frac{7}{5}\).
\(\frac{{ - 2}}{5}\).
\(\frac{9}{5}\).
\(\frac{3}{5}\).
Khẳng định nào sau đây là đúng?
\(0,125 \in \mathbb{Q}\).
\( - 10 \in \mathbb{N}\).
\(5\frac{1}{3} \notin \mathbb{Q}\).
\(3 \notin \mathbb{Z}\).
Cách biểu diễn số \(\frac{5}{3}\) trên trục số nào dưới đây là đúng?
A.  ;
;
B. 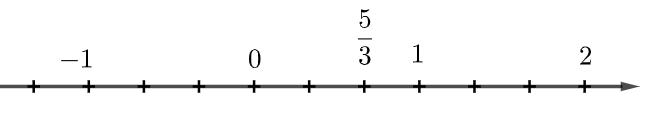 ;
;
C.  ;
;
D.  .
.
Số đối của số \( - \frac{{ - 3}}{5}\) là
\(\frac{5}{3}\).
\( - \frac{5}{3}\).
\( - \frac{3}{5}\).
\(\frac{3}{5}\).
Số đối của số hữu tỉ \[ - \frac{1}{4}\] là
\[4\].
\[ - 4\].
\(\frac{{ - 1}}{4}\).
\(\frac{1}{4}\).
Điền dấu thích hợp vào chỗ chấm \(3,25.... - 3\frac{4}{7}\) là
\( \le \).
=.
<.
>.
Các số \( - 2,15\,;\,\,\frac{5}{4};\,\, - 3\frac{1}{5};\,\,2\,;\,\,0\) được sắp xếp theo thứ tự giảm dần là
\[2;\,\,\frac{5}{4};\,\,0;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\[0;\,\,\frac{5}{4};\,\,2;\,\, - 2,15;\,\, - 3\frac{1}{5}\].
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,\frac{5}{4};\,\,2\).
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,2;\,\,\frac{5}{4}\).
Kết quả làm tròn đến chữ số thập phân thứ tư của \[\sqrt {17} \]là
\[4,1232\].
\[4,1231\].
\[4,1230\].
\[4,1233\].
Trong các số thập phân sau, số nào là số thập phân hữu hạn?
\[ - 5,348\].
\[ - 5,348...\].
\[ - 5,3\left( {48} \right)\].
\[ - 5,\left( {348} \right)\].
Trong các khẳng định sau, khẳng định nào đúng?
\[\sqrt {13} \in \mathbb{Q}\].
\[1,\left( 3 \right) \in \mathbb{N}\].
\[ - 3,456 \in \mathbb{Z}\].
\[\sqrt 5 \in \mathbb{R}\].
Kết quả của phép tính \(\frac{{{{20}^5}\,\,.\,\,{5^{10}}}}{{{{100}^5}}}\) là
3125.
1.
1225.
1525.
Trong các khẳng định sau, khẳng định nào đúng?
\[\frac{{ - 1}}{3} < - 0,5\].
\[\sqrt {\frac{{16}}{{25}}} = \frac{4}{5}\].
\[\sqrt {\frac{4}{9}} < \frac{1}{3}\].
\[1,2\left( 3 \right) = 1,23\].
Giá trị của\[x\] thỏa mãn \[\left| x \right| = 1,2\] là
\[x = - 1,2\].
\[x = 1,2\].
\[x \in \left\{ {1,2\,;\, - 1,2} \right\}\].
\[x = - \left( { - 1,2} \right)\].
Số nào sau đây là số thập phân vô hạn tuần hoàn?
\[1,25\].
\(\sqrt 5 \).
\[2,3\left( 4 \right)\].
\(\frac{{ - 3}}{4}\).
Trong các khẳng định sau, khẳng định nào là đúng?
Số vô tỉ không phải là số thập phân vô hạn không tuần hoàn;
Số vô tỉ là số được viết được dưới dạng số thập phân vô hạn không tuần hoàn;
Số vô tỉ cũng là số thập phân hữu hạn;
Số vô tỉ là số thập phân vô hạn tuần hoàn.
Hình lập phương không có đặc điểm nào sau đây?
Có 8 đường chéo.
Có 12 cạnh bằng nhau.
Có 6 mặt bằng nhau.
Có các mặt đều là hình vuông.
Cho hình hộp chữ nhật \[ABCD.EFGH\] (hình vẽ).
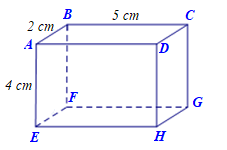
Biết \[AB = 2{\rm{ cm}}\], \(BC = 5\,{\rm{cm}}\), \(AE = 4\,\,{\rm{cm}}\).
Khẳng định nào sau đây là sai?
\[CD = 2{\rm{ cm}}\].
\(HG = 4\,\,{\rm{cm}}\).
\(GF = 5\,\,{\rm{cm}}\).
\(DH = 4\,\,{\rm{cm}}\).
Một hình lăng trụ đứng có đáy là tam giác đều. Số góc vuông được tạo bởi các cạnh trong hình lăng trụ đứng tam giác đó là
8.
10.
12.
24.
Cho tấm bìa như hình bên.
Khi sắp xếp độ dài các cạnh của mặt đáy theo thứ tự từ nhỏ đến lớn, ta được:
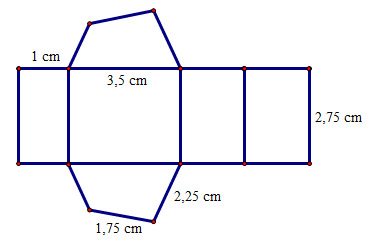
\[1{\rm{ cm}}\,{\rm{; }}1,75{\rm{ cm}}\,{\rm{; }}2,25{\rm{ cm}}\,{\rm{; }}3,5{\rm{ cm}}.\]
\[1{\rm{ cm}}\,{\rm{; }}1,75{\rm{ cm}}\,{\rm{; }}2,25{\rm{ cm}}\,{\rm{; }}2,75{\rm{ cm}}.\]
\[1{\rm{ cm}}\,{\rm{; }}1,75{\rm{ cm}}\,{\rm{; }}2,75{\rm{ cm}}\,{\rm{; }}3,5{\rm{ cm}}.\]
\[1{\rm{ cm}}\,{\rm{; }}2,25{\rm{ cm}}\,{\rm{; }}2,75{\rm{ cm}}\,{\rm{; }}3,5{\rm{ cm}}.\]
Trong các hình khai triển dưới đây, có bao nhiêu hình gấp lại được thành một hình lăng trụ đứng?
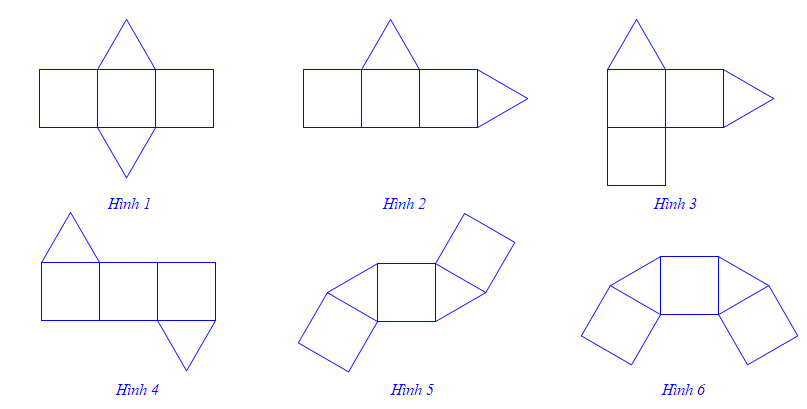
2.
3.
4.
5.
Cho hình hộp chữ nhật \[ABCD.MNPQ\] có độ dài \(NB = 3\,\,{\rm{cm}},\) \(BC = 4\,\,{\rm{cm}},\) \(MN = 2\,\,{\rm{cm}}\). Chiều dài mặt đáy hình hộp là
\(1\,\,{\rm{cm}}\).
\(2\,\,{\rm{cm}}\).
\(3\,\,{\rm{cm}}\).
\(4\,\,{\rm{cm}}\).
Cho tấm bìa như hình bên. Tấm bìa tạo lập được một hình lăng trụ đứng.
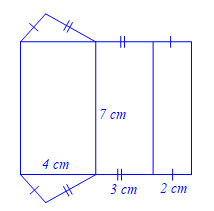
Chu vi đáy của hình lăng trụ đứng đó là
\(12\,\,{\rm{cm}}\).
\(11\,\,{\rm{cm}}\).
\(9\,\,{\rm{cm}}\).
\(22\,\,{\rm{cm}}\).
Khẳng định nào dưới đây đúng?
Hình lập phương có 8 cạnh, 12 đỉnh và 4 đường chéo.
Hình lập phương có 8 cạnh, 12 đỉnh và 6 đường chéo.
Hình lập phương có 8 đỉnh, 12 cạnh và 4 đường chéo.
Hình lập phương có 8 đỉnh, 12 cạnh và 6 đường chéo.
Công thức tính diện tích xung quanh của hình hộp chữ nhật có chiều dài là \(a,\) chiều rộng là \(b,\) chiều cao là \(h\) (\(a,\,\,b,\,\,h\) cùng đơn vị đo) là
\({S_{xq}} = 2\,\,.\,\,\left( {a + b} \right)\,\,.\,\,h\).
\({S_{xq}} = 2\,\,.\,\,\left( {a + h} \right)\,\,.\,\,b\).
\({S_{xq}} = 2\,\,.\,\,\left( {a + b + h} \right)\).
\({S_{xq}} = \left( {a + b} \right)\,\,.\,\,h\).
Cho hai góc \(\widehat {pAr}\) và \(\widehat {rAq}\) kề bù với nhau, biết \(\widehat {rAq} = 15^\circ \). Khi đó, số đo \(\widehat {pAr}\) bằng
\[15^\circ \].
\[165^\circ \].
\[75^\circ \].
\[90^\circ \].
Hai đường thẳng\(xx'\) và\(yy'\) cắt nhau tại \(O\). Góc đối đỉnh với \[\widehat {yOx'}\]là
\[\widehat {y'Ox'}\].
\[\widehat {y'Ox}\].
\[\widehat {yOx'}\].
\[\widehat {yOx}\].
Cho hai đường thẳng \(ab\) và \(cd\) cắt nhau tại \(O\) sao cho \(\widehat {aOc} = 120^\circ \). Khẳng định nào dưới đây làđúng?
\[\widehat {bOd} = 60^\circ \].
\[\widehat {bOc} = 60^\circ \].
\[\widehat {aOd} = 120^\circ \].
\[\widehat {bOc} = 120^\circ \].
Cho \(\widehat {mOn} = 110^\circ \), tia \(Ot\) là tia phân giác của \(\widehat {mOn}\). Khi đó, số đo \(\widehat {mOt}\) là
\[55^\circ \].
\[110^\circ \].
\[60^\circ \].
Một giá trị
Hai góc kề bù có tổng số đo bằng bao nhiêu?
\[90^\circ \].
\[180^\circ \].
\[45^\circ \].
\[30^\circ \].
Cho các bước vẽ tia phân giác \(Ot\)của \(\widehat {xOy} = 110^\circ \) bằng thước đo góc như sau:
(1)Đặt thước đo góc sao cho tâm của thước trùng với điểm \(O\) của tia \(Ox\) và tia \(Ox\) đi qua vạch \(0^\circ .\) Vẽ tia \(Oy\) đi qua vạch \(110^\circ \) của thước. Ta vẽ được \(\widehat {yOx} = 110^\circ \).
(2) Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên ta có \(\widehat {xOt} = \widehat {tOy} = \frac{{\widehat {xOy}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \). Do đó, đặt thước đo góc sao cho tâm của thước trùng với điểm \(O\) của tia \(Ox\) và tia \(Ox\) đi qua vạch \(0^\circ .\)Vẽ tia \(Ot\) đi qua vạch \(55^\circ \) và tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\), ta được tia phân giác \(Ot\) của \(\widehat {xOy}.\)
(3)Vẽ tia \(Ox.\)
Sắp xếp các bước trên để có thứ tự đúng các bước vẽ tia phân giác \(Ot\)của \(\widehat {xOy} = 110^\circ \) bằng thước đo góc là
(3) → (2) → (1).
(1) → (2) → (3).
(2) → (1) → (3).
(3) → (1) → (2).
Cho \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) là hai góc đối đỉnh. Biết \(\widehat {x'Oy'} = 45^\circ \) ta suy ra được góc \(xOy\) là
Góc nhọn;
Góc vuông;
Góc tù;
Góc bẹt.
Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]?
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1758501867.png)
B. ![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1758501878.png)
C. ![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/09/16-1758501890.png)
![Trong các hình vẽ sau, hình vẽ nào thể hiện tia \[Oz\] là tia phân giác của \[\widehat {xOy}\]? A. B. C. D. (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/09/17-1758501901.png)
Các cặp góc đối đỉnh trong hình bên là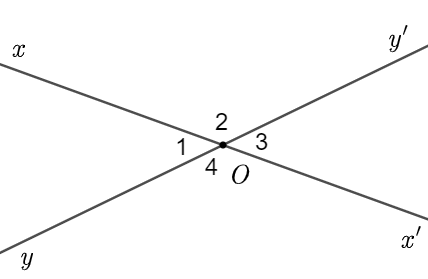
\({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_3}\).
\({\widehat O_1}\) và \({\widehat O_2}\); \({\widehat O_3}\) và \({\widehat O_4}\).
\({\widehat O_2}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_4}\).
\({\widehat O_1}\) và \({\widehat O_3}\); \({\widehat O_2}\) và \({\widehat O_4}\).








