Đề cương ôn tập giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Bài 3: Hàm số lượng giác và đồ thị
13 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tập xác định hàm số \(y = \sin x\) là:
\(D = {\rm{[}} - 1;1].\)
\(D = \mathbb{R}.\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in \mathbb{Z}} \right\}.\)
Mệnh đề nào sau đây là đúng?
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \[y = \cos x\] là hàm số chẵn.
Hàm số \(y = \tan x\)là hàm số chẵn.
Hàm số \(y = \cot x\) là hàm số chẵn.
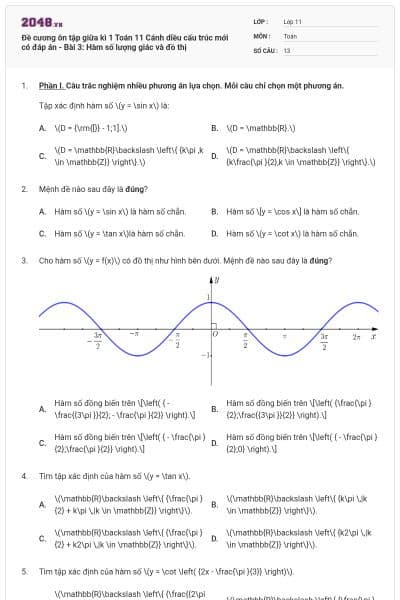
Cho hàm số \(y = f(x)\) có đồ thị như hình bên dưới. Mệnh đề nào sau đây là đúng?

Hàm số đồng biến trên \[\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right).\]
Hàm số đồng biến trên \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right).\]
Hàm số đồng biến trên \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right).\]
Hàm số đồng biến trên \[\left( { - \frac{\pi }{2};0} \right).\]
Tìm tập xác định của hàm số \(y = \tan x\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {k2\pi \,|k \in \mathbb{Z}} \right\}\).
Tìm tập xác định của hàm số \(y = \cot \left( {2x - \frac{\pi }{3}} \right)\).
\(\mathbb{R}\backslash \left\{ {\frac{{2\pi }}{3} + k\frac{\pi }{2}\,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{{2\pi }}{3} + k\pi \,|k \in \mathbb{Z}} \right\}\).
\(\mathbb{R}\backslash \left\{ {\frac{\pi }{6} + k\frac{\pi }{2}\,|k \in \mathbb{Z}} \right\}\).
Tập giá trị của hàm số \(y = 2\sin x\) là
\[\left[ { - 1;1} \right]\].
\[\left[ {0;2} \right]\].
\[\left\{ { - 2;2} \right\}\].
\[\left[ { - 2;2} \right]\].
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?

\[y = \tan x\].
\(y = \sin x\).
\[y = \cot x\].
\(y = \cos x\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \cos x\).
a) Hàm số đã cho có tập xác định là \(D = \left[ { - 1;1} \right]\).
b) Đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
c) Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng.
d) Hàm số đã cho nghịch biến trên khoảng \(\left( {0;\frac{{3\pi }}{2}} \right)\).
Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi muôi dưỡng các mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Giả sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức \(p\left( t \right) = 120 + 15\cos 150\pi t\), trong đó \(p\left( t \right)\) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời tian t tính theo đơn vị phút. Huyết áp cao nhất được gọi là huyết áp tâm thu và huyết áp thấp nhất được gọi là huyết áp tâm trương.
a) \( - 1 \le \cos 150\pi t,\forall t \ge 0\).
b) p(2) = 120 mmHg.
c) Huyết áp tâm thu của người đó là 135 mmHg
d) Huyết áp tâm trương của người đó là 105 mmHg.
Cho hàm số \(y = \sin x\) có đồ thị như hình
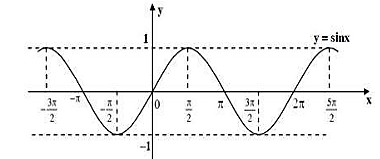
a) Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và đồng biến trên khoảng \(\left( {\frac{\pi }{2};\pi } \right)\).
b) Trên khoảng \(\left( { - \frac{\pi }{2};\frac{{5\pi }}{2}} \right)\) có 3 giá trị của \(x\) để \(\sin x = 0\).
c) Đường thẳng \(y = - 0,35\) giao với đồ thị hàm số \(y = \sin x\) tại 2 điểm phân biệt trên khoảng \(\left( { - \frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
d) Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {\frac{\pi }{7};\frac{\pi }{5}} \right)\).
Phần III. Trắc nghiệm trả lời ngắn
Tìm giá trị lớn nhất của hàm số \(y = - 4{\cos ^2}x + 2 + \pi \) (kết quả làm tròn đến hàng phần trăm).
Chiều cao so với mực nước biển trung bình tại thời điểm \(t\) (giây, \(t \ge 0\)) của mỗi cơn sóng được cho bởi hàm số \(h\left( t \right) = 75\sin \left( {\frac{{\pi t}}{8}} \right)\), trong đó \(h\left( t \right)\) được tính bằng centimét. Trong khoảng 15 giây đầu tiên (kể từ mốc t = 0 giây) thời điểm con sóng đạt cực đại là lúc \(t\) bằng bao nhiêu?
Số giờ có ánh sáng của thành phố T ở vĩ độ 40° bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An muốn đi tham quan thành phố T nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để thành phố T có ít giờ có ánh sáng mặt trời nhất?