Đề cương ôn tập giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
21 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Đường tròn lượng giác có bán kính bằng:
\[2\].
\[1\].
\[\frac{\pi }{2}\].
\[\pi \].
Khi quy đổi \(1^\circ \) ra đơn vị radian, ta được kết quả là
\(\pi \,{\rm{rad}}{\rm{.}}\)
\(\frac{{180}}{\pi }{\rm{rad}}{\rm{.}}\)
\(\frac{\pi }{{180}}{\rm{rad}}{\rm{.}}\)
\(\frac{\pi }{{360}}{\rm{rad}}{\rm{.}}\)
Gọi M là điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{{5\pi }}{6}\). Hỏi M thuộc góc phần tư thứ mấy?
II.
I.
IV.
III.
Số đo góc \(22^\circ 30'\) đổi sang rađian là:
\(\frac{\pi }{5}.\)
\(\frac{\pi }{8}{\rm{.}}\)
\(\frac{{7\pi }}{{12}}{\rm{.}}\)
\(\frac{\pi }{6}{\rm{.}}\)
Góc lượng giác nào sau đây có cùng điểm cuối với góc \(\frac{{7\pi }}{4}\)?
\( - \frac{\pi }{4}.\)
\(\frac{\pi }{4}{\rm{.}}\)
\(\frac{{3\pi }}{4}{\rm{.}}\)
\( - \frac{{3\pi }}{4}{\rm{.}}\)
Cho góc \(\alpha \) thỏa mãn \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây đúng?
\(\sin \alpha > 0\).
\(\cot \alpha < 0\).
\(\sin \alpha < 0\).
\(\cos \alpha < 0\).
Khẳng định nào sau đây đúng?
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
\({\sin ^2}\alpha + {\cos ^2}\alpha = 0\).
\({\sin ^2}\alpha + {\cos ^2}\alpha = 2\).
\({\sin ^2}\alpha + {\cos ^2}\alpha = - 1\).
Cho \(\sin \alpha = \frac{4}{5},\,\,\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
\(\cos \alpha = - \frac{3}{5}\).
\(\cos \alpha = \frac{1}{5}\).
\(\cos \alpha = \frac{3}{5}\).
\(\cos \alpha = \frac{1}{5}\).
Cho \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây đúng?
\(\sin \left( {\alpha - \pi } \right) \ge 0\).
\(\sin \left( {\alpha - \pi } \right) \le 0\).
\(\sin \left( {\alpha - \pi } \right) > 0\).
\(\sin \left( {\alpha - \pi } \right) < 0\).
Nếu \(\tan \alpha = \frac{3}{4}\) thì \({\sin ^2}\alpha \) bằng
\(\frac{{16}}{{25}}\).
\(\frac{9}{{25}}\).
\(\frac{{25}}{{16}}\).
\(\frac{{25}}{9}\).
Cho góc \(\alpha \) thỏa mãn \( - \frac{\pi }{2} < \alpha < 0\) và \(\cos \alpha = \frac{1}{2}\). Giá trị của biểu thức \(P = \sin \alpha + \frac{1}{{\cos \alpha }}\) bằng
\(\frac{{4 + \sqrt 3 }}{2}\).
\(\frac{{4 - \sqrt 3 }}{2}\).
\(\frac{{1 - \sqrt 3 }}{2}\).
\(\frac{{1 + \sqrt 3 }}{2}\).
Mệnh đề nào sau đây sai?
\(\sin (\pi + \alpha ) = \sin \alpha .\)
\(\cot (\pi + \alpha ) = \cot \alpha .\)
C. ![]() .
.
\(\tan (\pi + \alpha ) = \tan \alpha .\)
Trong các khẳng định sau, khẳng định nào sai?
\(\sin \left( {\pi - \alpha } \right) = \sin \alpha \).
\(\cos \left( {\pi - \alpha } \right) = \cos \alpha \).
\(\sin \left( {\pi + \alpha } \right) = - \sin \alpha \).
\(\cos \left( {\pi + \alpha } \right) = - \cos \alpha \).
Tính \(L = \tan 20^\circ .\tan 45^\circ .\tan 70^\circ \)
\(0\).
\(1\).
\( - 1\).
\(2\).
Biểu thức rút gọn của \(A = \frac{{{{\tan }^2}a - {{\sin }^2}a}}{{{{\cot }^2}a - {{\cos }^2}a}}\) ta được kết quả \(A = {\tan ^m}a\). Số thực m thuộc khoảng nào?
\(\left( { - \infty ;1} \right)\).
\(\left( {0;7} \right)\).
\(\left( {7;29} \right)\).
\(\left( {17; + \infty } \right)\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho \(\cos \alpha = - \frac{{\sqrt {15} }}{4}\) với \(\frac{\pi }{2} < \alpha < \pi \).
a) \(\sin \alpha < 0\).
b) \(\cos \left( {\pi - \alpha } \right) > 0\).
c) Biết \({\left( {\sin \alpha + 2\cos \alpha } \right)^2} = \frac{{a + b\sqrt {15} }}{{16}}\) với \(a,b \in \mathbb{Z}\). Khi đó \(a + b = 57\).
d) Giá trị của biểu thức \(B = 2\cos \alpha - 3\cos \left( {\pi - \alpha } \right) + 5\sin \left( {\frac{{7\pi }}{2} - \alpha } \right) + \cot \left( {\frac{{3\pi }}{2} - \alpha } \right)\) là \(\sqrt {15} \).
Cho góc lượng giác α có số đo theo đơn vị rađian là \(\frac{{3\pi }}{4}\).
a) Góc lượng giác α có số đo theo đơn vị độ là 155°.
b) Điểm biểu diễn góc lượng giác α là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I.
c) Góc lượng giác \( - \frac{{5\pi }}{4}\) có cùng điểm biểu diễn trên đường tròn lượng giác với góc α.
d) Góc lượng giác 855° có cùng điểm biểu diễn trên đường tròn lượng giác với góc α.
Trên đường tròn lượng giác tâm O và hệ trục tọa độ \(Oxy\) cho điểm M sao cho \(\widehat {AOM} = \frac{\pi }{3}\) như hình vẽ
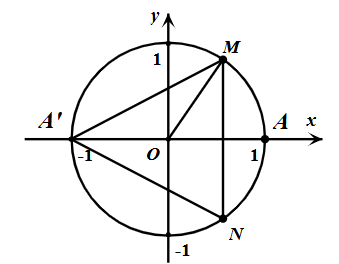
a) Số đo của các góc lượng giác có tia đầu là OA tia cuối là OM bằng \(\frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
b) Góc lượng giác có số đo \(\frac{{16\pi }}{3}\) có cùng tia đầu và tia cuối với góc lượng giác (OA, OM).
c) Trên đường tròn lượng giác, số điểm biểu diễn góc lượng giác có số đo \(\frac{\pi }{3} + \frac{{k\pi }}{2},k \in \mathbb{Z}\)là 6 điểm.
d) Khi biểu diễn góc \[\alpha = \frac{\pi }{3} + \frac{{k2\pi }}{3},k \in \mathbb{Z}\] lên đường tròn lượng giác ta được tập hợp điểm là một đa giác đều thì diện tích của đa giác đều đó bằng \(\frac{3}{4}\).
Phần III. Trắc nghiệm trả lời ngắn
Biết \(\cot \alpha = - 2\). Tính giá trị biểu thức \(A = \cos \left( {\alpha - \frac{\pi }{2}} \right) + \sin \left( {\alpha - \pi } \right) + \tan \left( {\pi + \alpha } \right)\).
Bánh xe của người đi xe đạp quay được 12 vòng trong 5 giây. Giả sử tại thời điểm bắt đầu quay van xe nằm ở vị trí V vuông góc với mặt đất. Hỏi trong một giây tia OV (O là trục bánh xe) quét một góc lượng giác bao nhiêu độ?

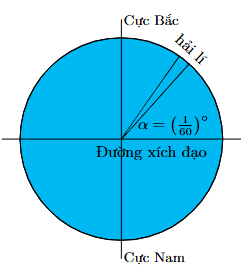
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc của đường kinh tuyến (như hình). Đổi số đo α sang rađian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là 6371 km (kết quả làm tròn đến hàng phần trăm).