Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 4. Tích vô hướng của hai vectơ
11 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác ABC đều. Góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) bằng
\(60^\circ .\)
\(120^\circ .\)
\(150^\circ .\)
\(30^\circ .\)
Cho hình bình hành \(ABCD\). Góc giữa 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là
\(\widehat {BAC}.\)
\(\widehat {ADC}.\)
\(\widehat {BAD}.\)
\(\widehat {ABC}.\)
Cho \(\overrightarrow a ,\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 4;\left| {\overrightarrow b } \right| = 5\) và \(\overrightarrow a .\overrightarrow b = 10\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 3 }}{2}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{1}{2}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{1}{2}\).
Cho tam giác ABC có \(\widehat {ABC} = 30^\circ ,AB = 5,BC = 8\). Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
\(20\).
\(20\sqrt 3 \).
\(20\sqrt 2 \).
\(40\sqrt 3 \).
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ,\widehat B = 60^\circ \) và \(AB = a\). Khi đó \(\overrightarrow {AC} .\overrightarrow {CB} \) bằng
\( - 2{a^2}\).
\(2{a^2}\).
\(3{a^2}\).
\( - 3{a^2}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình vuông ABCD có cạnh bằng a. Gọi M là trung điểm AB và O là tâm hình vuông.
a) \(\overrightarrow {AB} = \overrightarrow {BC} = a\).
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
c) \(\overrightarrow {AD} .\overrightarrow {AB} = \overrightarrow 0 \).
d) \(\overrightarrow {OA} .\overrightarrow {OM} = \frac{{{a^2}}}{4}\).
Cho tam giác ABC có AB = 2a, AC = 3a, \(\widehat {BAC} = 60^\circ \). Gọi I là trung điểm của đoạn thẳng BC. Điểm J thuộc đoạn AC thỏa mãn \(12AJ = 7AC\).
a) \(\overrightarrow {AB} .AC = 4{a^2}\).
b) \(\overrightarrow {AI} = \frac{3}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \).
c) \(\overrightarrow {BJ} = - \overrightarrow {AB} + \frac{7}{{12}}\overrightarrow {AC} \).
d)\(AI \bot BJ\).
Cho tam giác ABC đều cạnh a. Trên các cạnh BC, CA, AB lấy lần lượt các điểm M, N, P sao cho \(\overrightarrow {MC} = - 2\overrightarrow {MB} ,\overrightarrow {NA} = - \frac{1}{2}\overrightarrow {NC} \) và \(\overrightarrow {AP} = \frac{4}{{15}}\overrightarrow {AB} \).
a) Diện tích tam giác ABC là \(\frac{{{a^2}\sqrt 3 }}{2}\).
b) Độ dài của vectơ \(\overrightarrow {AB} + \overrightarrow {BC} = a\).
c)\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\).
d) \(\overrightarrow {AM} .\overrightarrow {PN} = 2{a^2}\).
Phần III. Trắc nghiệm trả lời ngắn
Cho tứ giác ABCD có AC = 5, BD = 4. Gọi M, N lần lượt là trung điểm của AD và BC, P và Q lần lượt là trung điểm của AB và CD. Giá trị của \(\overrightarrow {MN} .\overrightarrow {PQ} \) bằng bao nhiêu?
Cho tam giác ABC có độ dài cạnh AB = 4, BC = 5 và \(\widehat {ABC} = 120^\circ \). Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) có độ lớn \(\left| {\overrightarrow {{F_1}} } \right| = 10{\rm{N}},\left| {\overrightarrow {{F_2}} } \right| = 20{\rm{N}}\) và tạo với nhau một góc \(\left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) = 60^\circ \) cùng tác dụng lên một vật đặt tại điểm O làm cho vật di chuyển theo hướng từ O đến B (như hình vẽ). Biết OB = 100 m và chỉ có hai lưc \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) tác động lên vật.
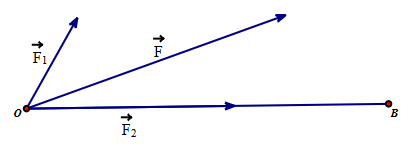
Tính công A của hợp lực \(\overrightarrow F \) của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) khi di chuyển vật từ O đến B?








