Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°
53 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác \(ABC\) có có \(a = 8\), \(c = 3\) và \(\widehat B = 60^\circ \). Độ dài cạnh \(b\) bằng
\(49\).
\(\sqrt {{\rm{97}}} \).
\(\sqrt {61} \).
\(7\).
Cho tam giác \(ABC\) có \(AB = 7\), \(AC = 8\) và \(\widehat A = 60^\circ \). Độ dài của cạnh \(BC\) bằng
\(7\).
\(47\).
\(\sqrt {57} \).
\(2\sqrt {57} \).
Cho \(\Delta ABC\) có \(AB = 13\,,\,\,AC = 8\) và \(BC = 7\). Tính số đo của góc \(\widehat {ACB}\).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
\(120^\circ \).
Tam giác \(ABC\) có \(\widehat B = 60^\circ \), \(\widehat C = 45^\circ \) và \(AB = 3\). Tính độ dài cạnh \(AC\).
\(3\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{2}\).
\(\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{4}\).
Cho tam giác ABC có BC = a, AC = b, AB = c. Gọi p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây đúng?
\(S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\).
\(S = 2bc\sin A\).
\(S = pr\).
\(S = \frac{{abc}}{{4r}}\).
Tam giác \(ABC\) có \(AB = 4\,,\,\,AC = 6\) và \(\widehat {BAC} = 30^\circ \). Tính diện tích tam giác \(ABC\).
\(6\).
\(3\).
\(6\sqrt 3 \).
\(3\sqrt 3 \).
Một tam giác có ba cạnh là 10, 12, 18. Diện tích tam giác bằng bao nhiêu?
\(42\sqrt 2 \).
\(40\sqrt 2 \).
\(40\sqrt 3 \).
\(41\sqrt 3 \).
Cho tam giác \(ABC\) có cạnh \(AB = 2\,{\rm{cm}}\), \(\widehat {ABC} = 60^\circ \) và \(\widehat {BAC} = 75^\circ \)(như hình vẽ bên dưới).
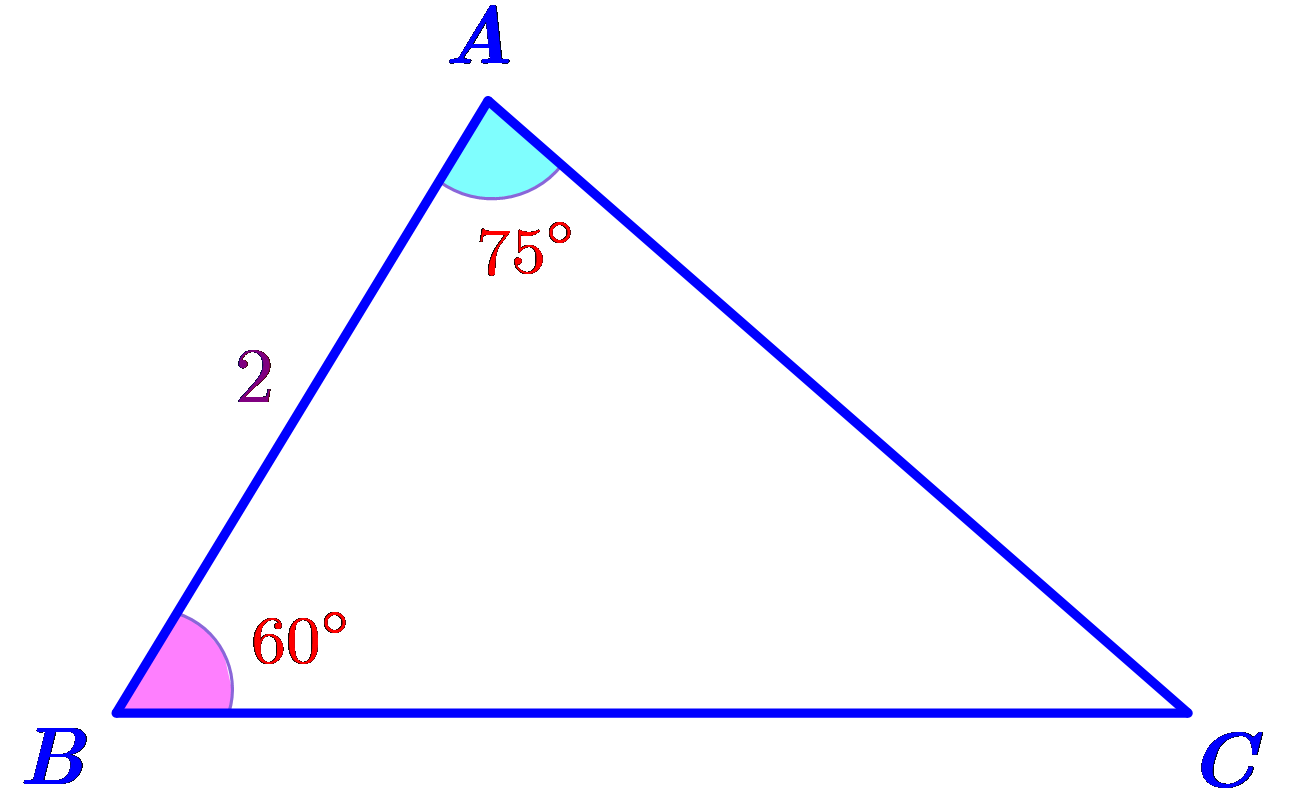
Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(0,63\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(2,45\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(1,58\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho tam giác \(ABC\) biết \(\widehat B = 45^\circ \) và \(\widehat C = 60^\circ \). Tỉ số \(\frac{{AB}}{{AC}}\) bằng
\(\frac{{\sqrt 6 }}{2}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\sqrt 6 \).
\(\frac{6}{5}\).
Cho tam giác nhọn \(ABC\) có \(\widehat A = 30^\circ \) và \(BC = 4\). Bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) bằng
\[R = 2\].
\[R = 3\].
\[R = 4\].
\[R = 5\].
Cho tam giác ABC có BC = a, AC = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 3 lần và giảm cạnh AB đi 2 lần, đồng thời giữ nguyên góc B thì khi đó diện tích tam giác mới được tạo thành bằng
\[2S\].
\[\frac{3}{2}S\].
\[6S\].
\[\frac{2}{3}S\].
Cho tam giác \(ABC\) có \(AB = 3\), \(BC = 5\) và độ dài đường trung tuyến \(BM = \sqrt {13} \). Bán kính \(r\) của đường tròn nội tiếp \[\Delta ABC\] bằng
\(2\).
\(\frac{1}{2}\).
\(1\).
\(\sqrt 2 \).
Tam giác \[ABC\] có \[BC = 12\], \[CA = 9\] và \[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho \[BM = 8\]. Tính độ dài đoạn thẳng \[AM\].
\(34\).
\(17\).
\(\sqrt {34} \).
\(\sqrt {43} \).
Trên biển một con thuyền thả neo ở vị trí A. Một người đứng ở vị trí K trên bờ biển muốn đo khoảng cách từ người đó đến con thuyền, người đó đã chọn một điểm H trên bờ với K và đo được KH = 380 m, \(\widehat {AKH} = 50^\circ ,\widehat {AHK} = 45^\circ \). Khoảng cách KA từ người đó đến con thuyền bằng
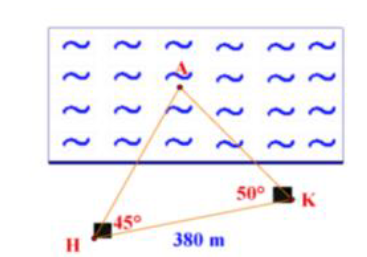
\(KA \approx 270\;{\rm{m}}\).
\(KA \approx 280\;{\rm{m}}\).
\(KA \approx 290\;{\rm{m}}\).
\(KA \approx 300\;{\rm{m}}\).
Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat {BAC} = 60^\circ \). Khi đó, bán kính đường tròn nội tiếp tam giác ABC bằng
\(1\).
\(2\).
\(\sqrt 3 \).
\(2\sqrt 3 \).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho tam giác \(ABC\) có \(AB = 3;AC = 2;\widehat A = 60^\circ \). Trên cạnh BC lấy điểm M nằm giữa B và C.
a) \(B{C^2} = A{B^2} + A{C^2} + 2AB.AC.\cos A\).
b) \(BC = \sqrt 7 \).
c) \(\cos B = \frac{{\sqrt 7 }}{7}\).
d) Độ dài AM nhỏ nhất bằng \(\frac{{189}}{{49}}\).
Cho tam giác ABC, biết AB = 13 cm, BC = 15 cm, \(\widehat B = 60^\circ \).
a) Công thức tính diện tích tam giác ABC là \(S = \frac{1}{2}BA.BC.\sin A\).
b) Diện tích tam giác ABC là \(S = \frac{{195\sqrt 3 }}{4}\) cm2.
c) Độ dài cạnh \(AC = \sqrt {199} \) cm.
d) Độ dài bán kính đường tròn nội tiếp của tam giác ABC là \(r = 2 + \sqrt 3 \) cm.
Cho tam giác ABC có a = 8; b = 6; c = 5.
a) Chu vi của tam giác ABC là 19.
b)\(\cos A = - \frac{1}{{20}}\).
c) Diện tích tam giác ABC là \(S = 14,98\) (kết quả làm tròn đến hàng phần trăm).
d) Bán kính đường tròn ngoại tiếp tam giác ABC là \(R = \frac{{320}}{{\sqrt {399} }}\).
Phần III. Trắc nghiệm trả lời ngắn
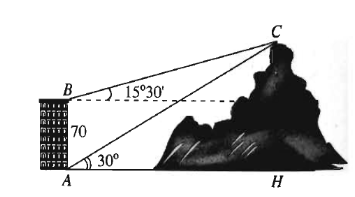
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao \(AB = 70\) m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi có độ cao so với mặt đất là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị).
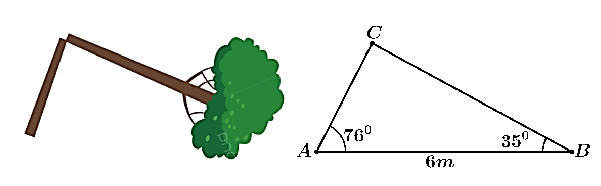
Một cái cây dạng thẳng đứng bị gió mạnh làm gãy không hoàn toàn (hai đoạn thân bị gãy vẫn dính liền nhau như hình vẽ). Một người muốn đo chiều cao của cây trước khi gãy, người ấy đo được đoạn thẳng nối từ gốc cây đến ngọn cây (đã ngã) là AB = 6 m, hai góc \(\widehat {CAB} = 76^\circ ;\widehat {CBA} = 35^\circ \). Tính chiều dài của cây trước khi bị gãy (giả sử sự biến hạng lúc dãy không ảnh hưởng đến tổng chiều dài của cây) (làm tròn kết quả cuối cùng đến hàng phần trăm không làm tròn các kết quả trung gian).
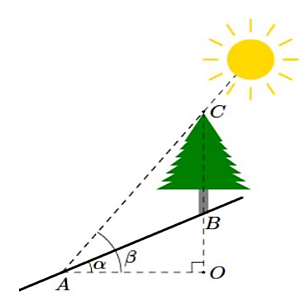
Trên sườn đồi có 1 cái cây thẳng đứng (tham khảo hình vẽ) đổ bóng dài AB = 39,5 m xuống đồi. Biết góc nghiêng của sườn đổi là \(\alpha = \widehat {OAB} = 26^\circ \) so với phương ngang và góc nâng của mặt trời là \(\beta = \widehat {OAC} = 50^\circ \). Tính chiều cao BC của cái cây (đơn vị tính là mét và làm tròn kết quả cuối cùng đến hàng đơn vị không làm tròn các kết quả trung gian).
B. TỰ LUẬN
Xét tính đúng sai của các mệnh đề sau và mệnh đề phủ định của nó.
a) \(\forall x \in \mathbb{R}:{x^2} > 0\);
b) \(\exists x \in \mathbb{R}:x > {x^2}\);
c) \(\forall n \in \mathbb{N},{n^2} + 1\) không chia hết cho 3.
a) Cho tập hợp \[M = \left\{ {x \in \mathbb{Z}\,\,\left| {\,\,\left( {{x^2} - 1} \right)\left( {2{x^2} - 3x - 2} \right) = 0} \right.} \right\}\]. Viết tập hợp \(M\) dưới dạng liệt kê.
b) Cho hai tập hợp \(A = \left( { - \,2\,;\,3} \right)\) và \(B = \left[ {1\,; + \,\infty } \right)\). Xác định các tập hợp \(A \cap B\) và \(A\backslash B\).
Biểu diễn các tập hợp sau trên trục số và tìm \(A \cap B;A \cup B;A\backslash B\).
a) \(A = \left[ { - 3;5} \right)\) và \(B = \left[ {1; + \infty } \right)\).
b) \(A = \left\{ {x \in \mathbb{R}|x \le 3} \right\}\) và \(B = \left\{ {x \in \mathbb{R}| - 2 < x < 2} \right\}\).
Cho 2 tập hợp \(A = \left[ {m - 10\,\,;\,\,m - 2} \right]\) và \(B = \left( {3\,;\,4} \right)\). Tìm tất cả các giá trị của tham số \(m\) để \(A \cap B = \emptyset \).
Cho các tập hợp \(A = \left( { - \infty ;m} \right)\) và \(B = \left[ {3m - 1;3m + 3} \right]\). Tìm \(m\) để:
a) \(A \cap B = \emptyset \); b) \(B \subset A\).
Biểu diễn miền nghiệm của các bất phương trình sau
a) \(2x - 4y \ge 6\); b) \(x - 3y < 0\).
Biểu diễn hình học tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \le 6\\x + y \le 4\\x \ge 0\\y \ge 0\end{array} \right.\).
Một xưởng sản xuất nước mắm, mỗi lít nước mắm loại I cần 3 kg cá và 2 giờ công lao động, đem lại mức lãi là 50 000 đồng; mỗi lít nước mắm loại II cần 2 kg cá và 3 giờ công lao động, đem lại mức lãi 40 000 đồng. Xưởng có 230 kg cá và cần làm việc trong 220 giờ. Hỏi xưởng đó nên sản xuất mỗi loại nước mắm bao nhiêu lít để có mức lãi cao nhất?
Trong một trận lụt ở Hội An, một khách sạn bị nước lụt tràn vào, cần di chuyển cùng một lúc 40 hành khách và 24 vali hành lý. Lúc này, ban quản lí khách sạn chỉ huy động được 8 chiếc ghe lớn và 8 chiếc ghe nhỏ. Một chiếc ghe lớn chỉ có thể chở 10 hành khách và 4 vali hành lý. Một chiếc ghe nhỏ chỉ có thể chở 5 hành khách và 4 vali hành lý. Giá một chuyến ghe lớn là 250 nghìn đồng và giá một chiếc ghe nhỏ là 130 nghìn đồng. Hỏi chủ khách sạn cần thuê bao nhiêu chiếc ghe mỗi loại để chi phí thấp nhất? Tính chi phí thấp nhất đó.
Tính giá trị của các biểu thức sau
a) \(M = \sin 45^\circ .\cos 45^\circ + \sin 30^\circ \); b) \(Q = \frac{1}{{{{\sin }^2}120^\circ }} - {\cot ^2}120^\circ \).
Cho \(0^\circ < \alpha < 90^\circ \) thỏa mãn \(\sin \alpha = \frac{3}{5}\). Tính \(\cos \alpha ,\tan \alpha ,\cot \alpha ,\sin \left( {180^\circ - \alpha } \right),\cos \left( {180^\circ - \alpha } \right).\)
Cho tam giác ABC có \(\widehat A = 120^\circ ,b = 8,c = 5\). Tính:
a) Cạnh a và các góc \(\widehat B,\widehat C\).
b) Diện tích tam giác ABC.
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Cho tam giác ABC có \(a = 15;b = 20;c = 25\).
a) Tính diện tích tam giác ABC.
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC.
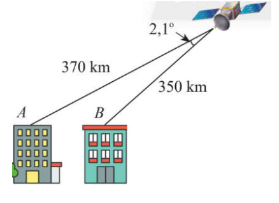
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ sinh đến A và B là \(2,1^\circ \).
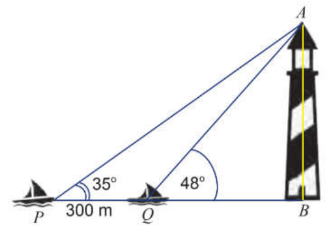
Hai chiếc tàu thủy P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng AB ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng AB dưới các góc \(\widehat {BPA} = 35^\circ \) và \(\widehat {BQA} = 48^\circ \). Tính chiều cao của tháp hải đăng đó.
Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN, các khoảng cách OM, ON và góc MON là đo được
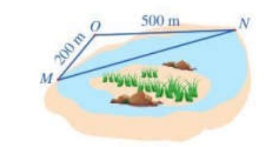
Sau khi đo, ta có OM = 200m, ON = 500m, \(\widehat {MON} = 135^\circ \). Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tính \(\cos 150^\circ \).
\(\frac{1}{2}\).
\[\frac{{\sqrt 3 }}{2}\].
\( - \frac{1}{2}\).
\( - \frac{{\sqrt 3 }}{2}\).
Cho hình bình hành \(ABCD\) như hình vẽ bên dưới. Biết rằng \(\cos \alpha = \frac{3}{5}\). Khi đó \(\cos \beta \) bằng
![Cho hình bình hành \(ABCD\) như hình vẽ bên dưới. Biết rằng \(\cos \alpha = \frac{3}{5}\). Khi đó \(\cos \beta \) bằng A. \(\frac{2}{5}\). B. \[ - \frac{3}{5}\]. C. \(\frac{4}{5}\). D. \(\frac{3}{5}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1758597283.png)
\(\frac{2}{5}\).
\[ - \frac{3}{5}\].
\(\frac{4}{5}\).
\(\frac{3}{5}\).
Cho góc \(90^\circ < \alpha < 180^\circ \). Biết rằng \(\sin \alpha = \frac{1}{3}\). Tính giá trị của \(\cos \alpha \).
\(\cos \alpha = \frac{2}{3}\).
\(\cos \alpha = - \frac{2}{3}\).
\(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
\(\cos \alpha = \frac{{ - 2\sqrt 2 }}{3}\).
Biết rằng điểm \(M\left( {a\,;\,b} \right)\) thoả mãn \[\widehat {MOx} = 30^\circ \] (hình vẽ minh hoạ). Khi đó giá trị của \(a\) bằng
![Biết rằng điểm \(M\left( {a\,;\,b} \right)\) thoả mãn \[\widehat {MOx} = 30^\circ \] (hình vẽ minh hoạ). Khi đó giá trị của \(a\) bằng A. \(\frac{3}{5}\). B. \(\frac{1}{2}\). C. \(\frac{{\sqrt 3 }}{2}\). D. \(\frac{4}{5}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1758597360.png)
\(\frac{3}{5}\).
\(\frac{1}{2}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{4}{5}\).
Cho 2 góc nhọn \(\alpha \) và \(\beta \) thoả mãn \(\alpha + \beta = 90^\circ \). Đẳng thức nào sau đây sai?
\(\sin \alpha = \cos \beta \).
\(\cos \alpha = - \sin \beta \).
\(\tan \alpha = \cot \beta \).
\(\cot \alpha = \tan \beta \).
Cho góc \(\alpha \) thoả mãn \(\sin \alpha = \frac{3}{5}\) và \(0^\circ < \alpha < 90^\circ \). Khi đó giá trị \(\cot \left( {180^\circ - \alpha } \right)\) bằng
\[\frac{4}{3}\].
\[\frac{3}{4}\].
\[ - \frac{4}{3}\].
\[ - \frac{3}{4}\].
Cho góc \(\alpha \) thỏa mãn \(0^\circ \le \alpha \le 180^\circ \). Khẳng định nào sau đây đúng?
\(\sin \left( {180^\circ - \alpha } \right) = \sin \alpha \).
\(\cos \left( {180^\circ - \alpha } \right) = \cos \alpha \).
\(\tan \left( {180^\circ - \alpha } \right) = \tan \alpha \).
\(\cot \left( {180^\circ - \alpha } \right) = \cot \alpha \).
Biết rằng \[\cos \alpha = \frac{1}{3}\]. Giá trị của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) là
\[\frac{1}{3}\].
\[\frac{{10}}{9}\].
\[\frac{{11}}{9}\].
\[\frac{4}{3}\].
Cho góc \(\alpha \) thỏa mãn \(\tan \alpha = 4\). Tính giá trị của biểu thức \[A = \frac{{\sin \alpha + \cos \alpha }}{{\sin \alpha - 3\cos \alpha }}\].
\(A = 1\).
\(A = \frac{1}{2}\).
\(A = \frac{1}{5}\).
\(A = 5\).
Kết quả rút gọn của biểu thức \({\left( {\frac{{\sin \alpha + \tan \alpha }}{{\cos \alpha + 1}}} \right)^2} + 1\) bằng
\(2\).
\(1 + \tan \alpha \).
\(\frac{1}{{{{\cos }^2}\alpha }}\).
\(\frac{1}{{si{n^2}\alpha }}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho \(\sin x = \frac{5}{{13}}\) và \(90^\circ < x < 180^\circ \).
a) \(\cos x > 0\).
b) Giá trị của biểu thức \(P = 2{\sin ^2}x - {\cos ^2}x = - \frac{{94}}{{169}}\).
c) Giá trị \(\tan x = \frac{5}{{12}}\).
d) Giá trị của biểu thức \(A = \frac{{{{\sin }^2}x}}{{1 + {{\cos }^2}x}} = \frac{{25}}{{313}}\).
Cho \(\tan \alpha = - 2\left( {90^\circ < \alpha < 180^\circ } \right)\). Khi đó:
a)\(\frac{{\sin \alpha - \cos \alpha }}{{2\sin \alpha + 3\cos \alpha }} = 3\).
b) \(\cos \alpha > 0\).
c) \({\cos ^2}\alpha = \frac{1}{5}\).
d)\(\sin \left( {180^\circ - \alpha } \right) = - \frac{{2\sqrt 5 }}{5}\).
Cho \(\sin \alpha = \frac{1}{3}\) với \(90^\circ < \alpha < 180^\circ \).
a) Giá trị \(\sin \alpha .\cos \alpha < 0\).
b) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\).
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
d) \(\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{2}{5}\).
Phần III. Trắc nghiệm trả lời ngắn
Cho \(\cot \alpha = 2\). Biết giá trị của biểu thức \(P = \frac{{3\sin \alpha + 4\cos \alpha }}{{\sqrt 2 \sin \alpha - \cos \alpha }} = \frac{{a - b\sqrt 2 }}{2}\left( {a,b \in \mathbb{Z}} \right)\). Tính \(a + 2b.\)
Tính \(S = {\cos ^2}5^\circ + {\cos ^2}10^\circ + {\cos ^2}15^\circ + ... + {\cos ^2}80^\circ + {\cos ^2}85^\circ \).
Cho tam giác \(ABC\). Giá trị biểu thức \(a = \sin \left( {A + B} \right)\sin C - \cos \left( {A + B} \right)\cos C\) là \(a \in \mathbb{N}\). Tính giá trị của \(2025a + 2026\).








