Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 2: Định lí côsin và định lí sin
18 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác \(ABC\) có có \(a = 8\), \(c = 3\) và \(\widehat B = 60^\circ \). Độ dài cạnh \(b\) bằng
\(49\).
\(\sqrt {{\rm{97}}} \).
\(\sqrt {61} \).
\(7\).
Cho tam giác \(ABC\), có độ dài ba cạnh là \(BC = a,AC = b,AB = c\). Gọi \(R\) là bán kính đường tròn ngoại tiếp tam giác và \(S\) là diện tích tam giác đó. Mệnh đề nào sau đây sai?
\[{a^2} = {b^2} + {c^2} - 2bc\cos A\].
\[\frac{{\sin A}}{a} = \frac{{\sin B}}{b} = \frac{{\sin C}}{c}\].
\[S = \frac{{abc}}{R}\].
\[S = \sqrt {p(p - a)(p - b)(p - c)} \].
Cho tam giác \(ABC\) thoả mãn: \[{b^2} + {c^2} - {a^2} = - \sqrt 2 bc\]. Khi đó:
\(\widehat A = 45^\circ .\)
\(\widehat A = 30^\circ .\)
\(\widehat A = 60^\circ .\)
\(\widehat A = 135^\circ \).
Cho tam giác ABC có BC = a, AC = b, AB = c. Gọi p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây đúng?
\(S = p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)\).
\(S = 2bc\sin A\).
\(S = pr\).
\(S = \frac{{abc}}{{4r}}\).
Tam giác \(ABC\) có \(AB = 4\,,\,\,AC = 6\) và \(\widehat {BAC} = 30^\circ \). Tính diện tích tam giác \(ABC\).
\(6\).
\(3\).
\(6\sqrt 3 \).
\(3\sqrt 3 \).
Một tam giác có ba cạnh là 10, 12, 18. Diện tích tam giác bằng bao nhiêu?
\(42\sqrt 2 \).
\(40\sqrt 2 \).
\(40\sqrt 3 \).
\(41\sqrt 3 \).
Cho tam giác \(ABC\) có cạnh \(AB = 2\,{\rm{cm}}\), \(\widehat {ABC} = 60^\circ \) và \(\widehat {BAC} = 75^\circ \)(như hình vẽ bên dưới).
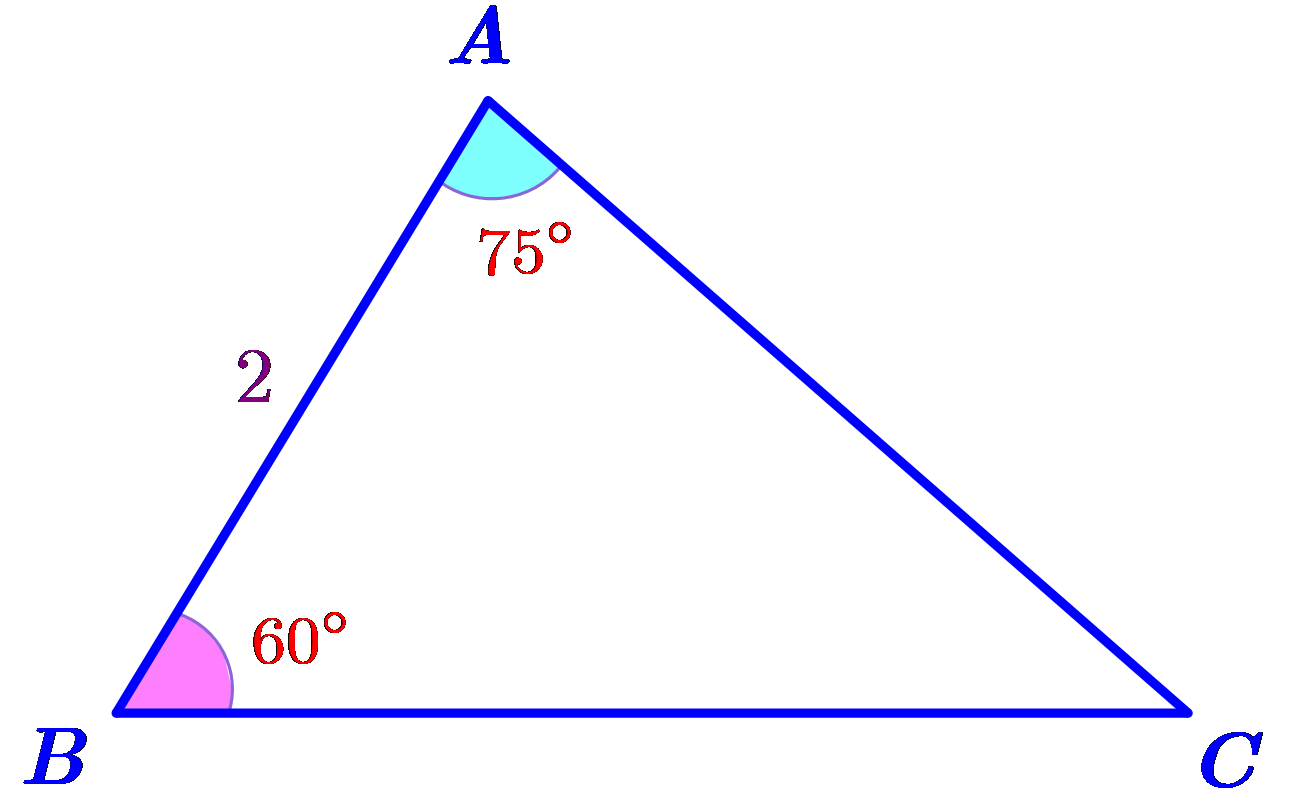
Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(0,63\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(2,45\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
\(1,58\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho tam giác \(ABC\) biết \(\widehat B = 45^\circ \) và \(\widehat C = 60^\circ \). Tỉ số \(\frac{{AB}}{{AC}}\) bằng
\(\frac{{\sqrt 6 }}{2}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\sqrt 6 \).
\(\frac{6}{5}\).
Cho tam giác nhọn \(ABC\) có \(\widehat A = 30^\circ \) và \(BC = 4\). Bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) bằng
\[R = 2\].
\[R = 3\].
\[R = 4\].
\[R = 5\].
Cho tam giác ABC có BC = a, AC = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 3 lần và giảm cạnh AB đi 2 lần, đồng thời giữ nguyên góc B thì khi đó diện tích tam giác mới được tạo thành bằng
\[2S\].
\[\frac{3}{2}S\].
\[6S\].
\[\frac{2}{3}S\].
Cho tam giác \(ABC\) có \(AB = 3\), \(BC = 5\) và độ dài đường trung tuyến \(BM = \sqrt {13} \). Bán kính \(r\) của đường tròn nội tiếp \[\Delta ABC\] bằng
\(2\).
\(\frac{1}{2}\).
\(1\).
\(\sqrt 2 \).
Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat {BAC} = 60^\circ \). Khi đó, bán kính đường tròn nội tiếp tam giác ABC bằng
\(1\).
\(2\).
\(\sqrt 3 \).
\(2\sqrt 3 \).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho tam giác \(ABC\) có \(AB = 3;AC = 2;\widehat A = 60^\circ \). Trên cạnh BC lấy điểm M nằm giữa B và C.
a) \(B{C^2} = A{B^2} + A{C^2} + 2AB.AC.\cos A\).
b) \(BC = \sqrt 7 \).
c) \(\cos B = \frac{{\sqrt 7 }}{7}\).
d) Độ dài AM nhỏ nhất bằng \(\frac{{189}}{{49}}\).
Cho tam giác ABC, biết AB = 13 cm, BC = 15 cm, \(\widehat B = 60^\circ \).
a) Công thức tính diện tích tam giác ABC là \(S = \frac{1}{2}BA.BC.\sin A\).
b) Diện tích tam giác ABC là \(S = \frac{{195\sqrt 3 }}{4}\) cm2.
c) Độ dài cạnh \(AC = \sqrt {199} \) cm.
d) Độ dài bán kính đường tròn nội tiếp của tam giác ABC là \(r = 2 + \sqrt 3 \) cm.
Cho tam giác ABC có a = 8; b = 6; c = 5.
a) Chu vi của tam giác ABC là 19.
b) \(\cos A = - \frac{1}{{20}}\).
c) Diện tích tam giác ABC là \(S = 14,98\) (kết quả làm tròn đến hàng phần trăm).
d) Bán kính đường tròn ngoại tiếp tam giác ABC là \(R = \frac{{320}}{{\sqrt {399} }}\).
Phần III. Trắc nghiệm trả lời ngắn
Cho tam giác ABC có c = 3; b = 5; a = 6. Tính diện tích tam giác ABC (kết quả làm tròn đến hàng phần trăm).
Cho tam giác ABC biết b = 7, c = 5, \(\cos A = \frac{3}{5}\). Biết rằng bán kính đường tròn nội tiếp tam giác ABC có dạng \(r = a - \sqrt b \), trong đó \(a,b \in \mathbb{N}\). Tính giá trị biểu thức \(a - 2b\).
Cho hình thoi ABCD có cạnh bằng 1. Góc \(\widehat {BAD} = 30^\circ \). Tính diện tích hình thoi ABCD.








