Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 3: Giải tam giác và các ứng dụng thực tế
10 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho tam giác \(ABC\) có \(AB = 7\), \(AC = 8\) và \(\widehat A = 60^\circ \). Độ dài của cạnh \(BC\) bằng
\(7\).
\(47\).
\(\sqrt {57} \).
\(2\sqrt {57} \).
Cho \(\Delta ABC\) có \(AB = 13\,,\,\,AC = 8\) và \(BC = 7\). Tính số đo của góc \(\widehat {ACB}\).
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
\(120^\circ \).
Tam giác \(ABC\) có \(\widehat B = 60^\circ \), \(\widehat C = 45^\circ \) và \(AB = 3\). Tính độ dài cạnh \(AC\).
\(3\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{2}\).
\(\sqrt 6 \).
\(\frac{{3\sqrt 6 }}{4}\).
Tam giác \[ABC\] có \[BC = 12\], \[CA = 9\] và \[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho \[BM = 8\]. Tính độ dài đoạn thẳng \[AM\].
\(34\).
\(17\).
\(\sqrt {34} \).
\(\sqrt {43} \).
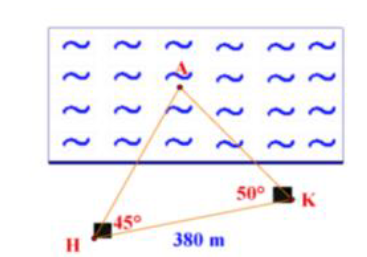
Trên biển một con thuyền thả neo ở vị trí A. Một người đứng ở vị trí K trên bờ biển muốn đo khoảng cách từ người đó đến con thuyền, người đó đã chọn một điểm H trên bờ với K và đo được KH = 380 m, \(\widehat {AKH} = 50^\circ ,\widehat {AHK} = 45^\circ \). Khoảng cách KA từ người đó đến con thuyền bằng
\(KA \approx 270\;{\rm{m}}\).
\(KA \approx 280\;{\rm{m}}\).
\(KA \approx 290\;{\rm{m}}\).
\(KA \approx 300\;{\rm{m}}\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Hai người dân đứng cách nhau 30 m cùng nhìn lên đỉnh của một tòa nhà theo góc nhìn lần lượt là 30° và 50°.
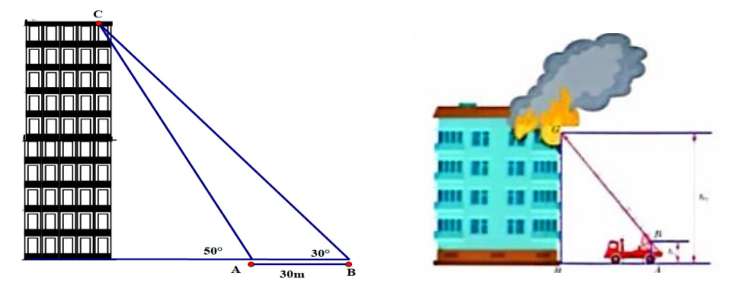
a) Góc nhìn từ đỉnh tòa nhà về hai phía A và B nơi hai người dân đang đứng là góc \(\widehat {ACB}\) có số đo 30°.
b) Khoảng cách từ vị trí người A tới nóc của tòa nhà là 43,9 m.
c) Chiều cao của tòa nhà là khoảng 30 m.
d) Vì gặp sự cố nên tầng trên cùng của tòa nhà đang bị cháy. Để cứu hộ đám cháy, một xe cứu hỏa đã tiếp cận dưới chân tòa nhà và chân thang đứng cách mặt đất 1,8 m, chiều dài tối đa của thang xếp là 40 m. Để tiếp cận được đám cháy thì xe cứu hỏa phải đứng cách chân tòa nhà một khoảng xa nhất là 21,7 m.
Một người quan sát đứng cách một cái tháp 10 m, nhìn thẳng cái tháp dưới một góc 55° và được phân tích như trong hình bên dưới:
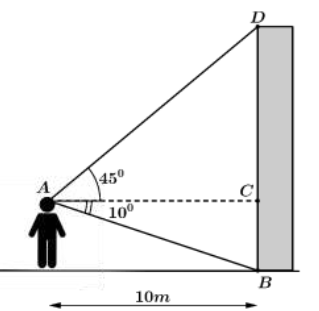
a) Số đo của góc \(\widehat {ADC} = 45^\circ \).
b) Độ dài đoạn AB xấp xỉ bằng 11,15 m.
c) Diện tích DACD bằng 100 m2.
d) Chiều cao của tháp xấp xỉ bằng 11,76 m.
Phần III. Trắc nghiệm trả lời ngắn
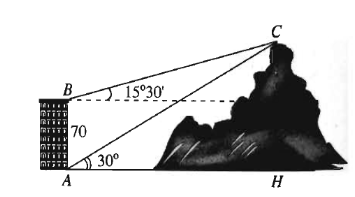
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao \(AB = 70\) m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi có độ cao so với mặt đất là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị).
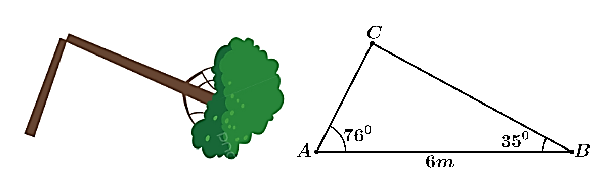
Một cái cây dạng thẳng đứng bị gió mạnh làm gãy không hoàn toàn (hai đoạn thân bị gãy vẫn dính liền nhau như hình vẽ). Một người muốn đo chiều cao của cây trước khi gãy, người ấy đo được đoạn thẳng nối từ gốc cây đến ngọn cây (đã ngã) là AB = 6 m, hai góc \(\widehat {CAB} = 76^\circ ;\widehat {CBA} = 35^\circ \). Tính chiều dài của cây trước khi bị gãy (giả sử sự biến hạng lúc dãy không ảnh hưởng đến tổng chiều dài của cây) (làm tròn kết quả cuối cùng đến hàng phần trăm không làm tròn các kết quả trung gian).
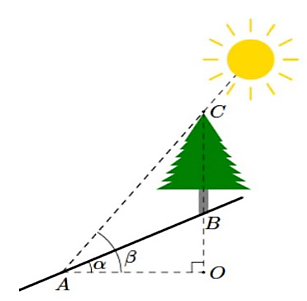
Trên sườn đồi có 1 cái cây thẳng đứng (tham khảo hình vẽ) đổ bóng dài AB = 39,5 m xuống đồi. Biết góc nghiêng của sườn đổi là \(\alpha = \widehat {OAB} = 26^\circ \) so với phương ngang và góc nâng của mặt trời là \(\beta = \widehat {OAC} = 50^\circ \). Tính chiều cao BC của cái cây (đơn vị tính là mét và làm tròn kết quả cuối cùng đến hàng đơn vị không làm tròn các kết quả trung gian).