Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 1. Khái niệm vectơ
11 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Vectơ có điểm đầu là D và điểm cuối là E được kí hiệu là:
\(DE\).
\(\left| {\overrightarrow {DE} } \right|\).
\(\overrightarrow {ED} \).
\(\overrightarrow {DE} \).
Mệnh đề nào sau đây đúng
Có duy nhất một vectơ cùng phương với mọi vectơ.
Có ít nhất hai vectơ cùng phương với mọi vectơ.
Có vô số vectơ cùng phương với mọi vectơ.
Không có vectơ nào cùng phương với mọi vectơ.
Gọi \(M;N\) lần lượt là trung điểm các cạnh AB; AC của tam giác đều ABC. Hỏi cặp vectơ nào sau đây cùng hướng.
\(\overrightarrow {MN} \) và \(\overrightarrow {CB} \).
\(\overrightarrow {AB} \) và \(\overrightarrow {MB} \).
\(\overrightarrow {MA} \) và \(\overrightarrow {MB} \).
\(\overrightarrow {AN} \) và \(\overrightarrow {CA} \).
Hai vectơ được gọi là bằng nhau khi và chỉ khi
Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
Chúng cùng hướng và độ dài của chúng bằng nhau.
Cho hình thoi \(ABCD\) cạnh \(a\) và \(\widehat {BAD} = 60^\circ \). Đẳng thức nào sau đây đúng?
\(\overrightarrow {AB} = \overrightarrow {AD} \).
\(\left| {\overrightarrow {BD} } \right| = a\).
\(\overrightarrow {BD} = \overrightarrow {AC} \).
\(\overrightarrow {BC} = \overrightarrow {DA} \).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho tam giác ABC có M và N lần lượt là trung điểm của AB và AC. Lấy điểm P đối xứng với điểm M qua N. Khi đó
a) MN = BC.
b) \(\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {MN} } \right|\).
c)\(\overrightarrow {MN} \) và \(\overrightarrow {BC} \) ngược hướng.
d)\(\overrightarrow {MP} = \overrightarrow {BC} \).
Cho hình chữ nhật ABCD tâm O.
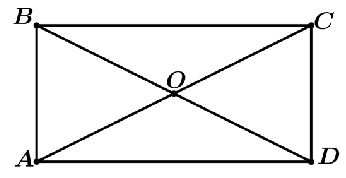
a) \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương.
b) \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\).
c)\(\overrightarrow {AC} = \overrightarrow {BD} \).
d) \(\overrightarrow {OA} = \overrightarrow {OC} \).
Cho tam giác ABC. Hãy dựng các điểm M, N sao cho \(\overrightarrow {AM} = \overrightarrow {BC} \), \(\overrightarrow {AN} = \overrightarrow {CB} \). Khi đó:
a) \(\overrightarrow {AM} \) ngược hướng với \(\overrightarrow {BC} \).
b) ABCM là hình bình hành.
c) ACBN là hình bình hành.
d) \(\overrightarrow {AM} ,\overrightarrow {AN} \) là hai vectơ đối nhau.
Phần III. Trắc nghiệm trả lời ngắn
Cho tam giác đều ABC có cạnh bằng 3. Gọi M, N lần lượt là trung điểm của AB và AC. Tính độ dài vectơ \(\overrightarrow {MN} \).
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của AB, AC và BC. Có bao nhiêu vectơ khác vectơ không có điểm đầu và điểm cuối là các điểm trong các điểm A, B, C, M, N, P bằng vectơ \(\overrightarrow {MN} \) (không trùng với \(\overrightarrow {MN} \)).
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Có bao nhiêu vectơ tạo thành từ các điểm đã cho cùng hướng với vectơ \(\overrightarrow {MN} \).








