Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 2. Tổng và hiệu của hai vectơ
16 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cho hình bình hành \(ABCD\),với giao điểm hai đường chéo là \(I\). Khi đó:
\(\overrightarrow {AB} + \overrightarrow {IA} = \overrightarrow {BI} \).
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \).
\(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\).
\(\overrightarrow {AB} + \overrightarrow {BD} = \vec 0\).
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm \(O\) là trung điểm của đoạn \(AB\).
\(OA = OB\).
\(\overrightarrow {OA} = \overrightarrow {OB} \).
\(\overrightarrow {AO} = \overrightarrow {BO} \).
\(\overrightarrow {OA} + \overrightarrow {OB} = \vec 0\).
Cho tam giác đều \[ABC\] cạnh \[a\]. Khi đó \[\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \]
\[a\sqrt 3 \].
\[\frac{{a\sqrt 3 }}{2}\].
\[2a\].
\[a\].
Kết quả bài toán tính\[\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {DA} + \overrightarrow {BC} \] là
\[\overrightarrow {D\,B} \].
\[2\,\overrightarrow {BD} \].
\[\overrightarrow 0 \].
\[ - \,\overrightarrow {AD} \].
Cho hình bình hành \(ABCD\) tâm \(O\). Khi đó \(\overrightarrow {OA} + \overrightarrow {BO} = \)
\(\overrightarrow {OC} + \overrightarrow {OB} \).
\(\overrightarrow {AB} \).
\(\overrightarrow {OC} + \overrightarrow {DO} \).
\(\overrightarrow {CD} \).
Cho 4 điểm bất kỳ\[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}O\]. Đẳng thức nào sau đây là đúng:
\[\overrightarrow {OA} = \overrightarrow {CA} - \overrightarrow {CO} \].
\[\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {BC} \].
\[\overrightarrow {AB} = \overrightarrow {OB} + \overrightarrow {OA} \].
\[\overrightarrow {OA} = \overrightarrow {OB} - \overrightarrow {BA} \].
Gọi \[G\]là trọng tâm tam giác vuông \[ABC\;\]với cạnh huyền\[BC = 12\]. Vectơ \[\overrightarrow {GB} - \overrightarrow {CG} \] có độ dài bằng bao nhiêu?
\[2\].
\[4\].
\[8\].
\[2\sqrt 3 \].
Cho hình vuông \[ABCD\]cạnh\[a\], độ dài vectơ \[\overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {BD} \]bằng:
\[a\].
\[3a\].
\[a\sqrt 2 \].
\[2a\sqrt 2 \].
Cho đường tròn \(O\) và hai tiếp tuyến song song với nhau tiếp xúc với \(\left( O \right)\) tại hai điểm \(A\) và \(B\). Mệnh đề nào sau đây đúng?
\(\overrightarrow {OA} = - \overrightarrow {OB} .\)
\(\overrightarrow {AB} = - \overrightarrow {OB} .\)
\(OA = - OB.\)
\(AB = - BA.\)
Cho hình bình hành \(ABCD.\) Gọi \(G\) là trọng tâm của tam giác \(ABC\). Mệnh đề nào sau đây đúng?
\(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {BD} .\)
\[\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {CD} .\]
\[\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow O .\]
\[\overrightarrow {GA} + \overrightarrow {GD} + \overrightarrow {GC} = \overrightarrow {CD} .\]
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hình thoi ABCD với cạnh có độ dài bằng 5 và \(\widehat {ABC} = 120^\circ \). Gọi O là giao điểm của AC và BD. Khi đó:
a) \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \) là hai vectơ đối nhau.
b)\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OC} - \overrightarrow {OD} \).
c) Với M là điểm bất kì, ta có \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MC} + \overrightarrow {MD} \).
d) \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 5\sqrt 3 \).
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC.
a) \(\overrightarrow {AM} - \overrightarrow {AN} = \overrightarrow {NM} \).
b)\(\overrightarrow {MN} - \overrightarrow {NC} = \overrightarrow {MP} \).
c) \(\overrightarrow {MN} - \overrightarrow {PN} = \overrightarrow {MP} \).
d) \(\overrightarrow {BP} - \overrightarrow {CP} = \overrightarrow {PC} \).
Cho hình vuông ABCD cạnh a, có O là giao điểm hai đường chéo. Khi đó:
a) O là trung điểm AC, BD.
b) \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right| = a\sqrt 2 \).
c)\(\left| {\overrightarrow {AB} + \overrightarrow {DC} } \right| = a\).
d) \(\left| {\overrightarrow {CD} - \overrightarrow {DA} } \right| = \frac{{a\sqrt 2 }}{2}\).
Phần III. Trắc nghiệm trả lời ngắn
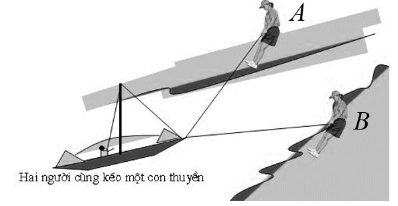
Hai người đứng hai bên bờ kênh, cùng kéo một chiếc thuyền xuôi trên kênh. Người A kéo với một lực bằng 60 N, người B kéo với một lực bằng 80 N, hai lực hợp nhau một góc bằng 90°. Vậy hợp lực mà hai người đã tác động lên thuyền có độ lớn bằng bao nhiêu?
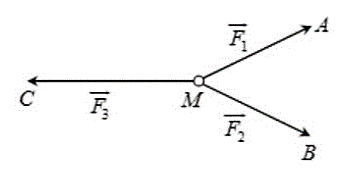
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng 100 và \(\widehat {AMB} = 60^\circ \). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (kết quả làm tròn đến hàng đơn vị).
Cho hình vuông ABCD cạnh 2, M là trung điểm BC. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {BM} } \right|\) (kết quả làm tròn đến hàng đơn vị).








