Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 2: Tập hợp
32 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Tập hợp nào sau đây là tập con của tập hợp \(A = \left\{ {0\,;\,1\,;\,2\,;\,3} \right\}\)?
\(\left\{ {0\,;\,1\,;\,2\,;\,4} \right\}\).
\(\left\{ {0\,;\,1} \right\}\).
\(\left\{ {0\,;\,1\,;\, - 1} \right\}\).
\(\left\{ {0\,;\,1\,;\,2\,;\,3\,;\, - 1} \right\}\).
Cho tập \(X = \left\{ {1;2;3;4} \right\}\). Câu nào sau đây đúng?
Số tập con của X là 16.
Số tập con có hai phần tử của X là 8.
Số tập con chứa số 1 của X là 6.
Số tập con chứa 4 phần tử của X là 0.
Cho tập hợp \[A = \left\{ {\left. {x \in \mathbb{N}\,} \right|} \right.\]\(x\) là số nguyên tố nhỏ hơn \(\left. {10} \right\}\). Tập \(A\) bằng tập hợp nào sau đây?
\(Q = \left\{ {1\,;2\,;\,3\,;\,5\,;7} \right\}\).
\(M = \left\{ {1\,;\,3\,;\,4\,;\,5} \right\}\).
\(P = \left\{ {0\,;\,2\,;\,3\,;\,5\,;\,7} \right\}\).
\(N = \left\{ {2\,;3\,;5\,;7} \right\}\).
Cho tập hợp \(A = \left\{ {\left. {x \in \mathbb{N}\,} \right|\,\,\left( {2x + 6} \right)\left( {x - 3} \right) = 0} \right\}\). Số phần tử của tập hợp \(A\) là
\[0\].
\[1\].
\[3\].
\[2\].
Hãy liệt kê các phần tử của tập hợp \[X = \left\{ {x \in \mathbb{Z}\,\left| {\,2{x^2} - 5x + 2 = 0} \right.} \right\}\].
\(X = \left\{ 0 \right\}\).
\(X = \left\{ {\frac{1}{2}} \right\}\).
\(X = \left\{ 2 \right\}\).
\(X = \left\{ {2\,;\frac{1}{2}} \right\}\).
Cho tập hợp\(A = \left( { - \infty \,;3} \right]\) và \(B = \left( {1\,;5} \right]\). Khi đó tập hợp \(A \cup B\) là
\(\left( {1\,;3} \right]\).
\[\left( {3\,;5} \right]\].
\(\left( { - \infty \,;5} \right]\).
\(\left( { - \infty \,;1} \right)\).
Cho hai tập hợp \(A = \left[ {0\,;3} \right]\) và \(B = \left( {1\,;4} \right)\). Tìm tập hợp \(A \cap B\).
\(\left( {1\,;3} \right]\).
\(\left[ {0\,;4} \right)\).
\(\left[ {0\,;1} \right]\).
\(\left( {3\,;4} \right)\).
Cho hai tập hợp \[A = \left\{ {1\,;3\,;5\,;7} \right\}\] và \[B = \left\{ {1\,;2\,;3\,;4\,;5\,;6} \right\}\]. Tập hợp \(B\backslash A\) có số phần tử là
\(1\).
\(4\).
\(2\).
\(3\).
Cho tập hợp \(A = \left[ {2\,; + \infty } \right)\). Tập hợp \({C_\mathbb{R}}A\) bằng
\(\left( { - \infty \,;2} \right)\).
\(\left( { - \infty \,;2} \right]\).
\(\left[ { - \infty \,;2} \right]\).
\(\left( {2\,; + \infty } \right)\).
Cho \(A\) là tập hợp các ước nguyên dương của 9, \(B\) là tập hợp các ước nguyên dương của 12. Khi đó tập hợp \(A \cap B\) là
\(A \cap B = \left\{ {1\,;\,2\,;\,3\,;4\,;\,6\,;\,9\,;\,12} \right\}\).
\(A \cap B = \left\{ 3 \right\}\).
\(A \cap B = \left\{ 6 \right\}\).
\(A \cap B = \left\{ {1\,;\,3} \right\}\).
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}\,} \right|\,\,4 \le x \le 9} \right\}\) được kết quả là
\(\left[ {4\,;9} \right]\).
\(\left( {4\,;9} \right]\).
\(\left[ {4\,;9} \right)\).
\(\left( {4\,;9} \right)\).
Cho \(A = \left\{ {0\,;1\,;2\,;3\,;4} \right\},\,\,B = \left\{ {2\,;3\,;4\,;5\,;6} \right\}\). Tập hợp \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) bằng
\(\left\{ {2\,;3\,;4} \right\}\).
\(\left\{ {5\,;6} \right\}\).
\(\left\{ {0\,;1\,;5\,;6} \right\}\).
\(\left\{ {1\,;2} \right\}\).
Cho tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}} \right| - 2 \le x < 3} \right\}\) và \(\mathbb{N}\) là tập hợp các số tự nhiên. Khi đó tập hợp \(A \cap \mathbb{N}\) bằng
\(\left[ { - 2\,;\,2} \right)\).
\(\left\{ {1\,;2} \right\}\).
\(\left[ {0\,;\,3} \right).\)
\(\left\{ {0\,;1\,;2} \right\}\).
Cho \(A = \left( {2\,;\; + \infty } \right)\) và \(B = \left( {m\,;\; + \infty } \right)\). Điều kiện cần và đủ của \(m\) để \(B \subset A\) là
\(m \ge 2\).
\(m \le 2\).
\(m = 2\).
\(m > 2\).
Cho các tập hợp \[A = \left( { - \infty \,;3} \right)\]và \[B = \left[ {0\,;10} \right]\]. Số phần tử là số nguyên của tập hợp \[B\backslash A\] là
\[6\].
\[7\].
\[8\].
vô số.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hai tập hợp A = {0; 1; 2; 3; 4}; B = {3; 4; 5; 6}.
a) A B = {0; 1; 2; 3; 4; 5; 6}.
b) A B = {5; 6}.
c) B\A = {0; 1; 2}.
d) (A B)\ (A B) = (A\B) (B\A).
Cho ba tập hợp \(A = \left( {1;\frac{{11}}{2}} \right);B = \left[ { - 2;3} \right]\) và \(C = \left( {\frac{{m - 1}}{3}; + \infty } \right)\).
a) Giao của hai tập hợp A và B là \(\left( {1;3} \right]\).
b) Tập hợp B ℕ gồm 6 phần tử.
c) Tập hợp \(\mathbb{R}\backslash A = \left( { - \infty ;1} \right] \cup \left[ {\frac{{11}}{2}; + \infty } \right)\).
d) Tổng các giá trị nguyên của \(m\) để \(B \cap C\) có đúng 3 phần tử là số nguyên bằng 6.
Lớp 10A có 18 học sinh tham gia câu lạc bộ bóng đá và 15 học sinh tham gia câu lạc bộ bóng rổ. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên. Khi đó:
a) Có 8 học sinh tham gia câu lạc bộ bóng đá và không tham gia câu lạc bộ bóng rổ.
b) Có 23 học sinh tham gia ít nhất một trong hai câu lạc bộ trên.
c) Biết lớp 10A có 45 học sinh. Có 25 học sinh không tham gia câu lạc bộ bóng đá.
d) Biết lớp 10A có 45 học sinh. Có 24 học sinh không giam gia cả hai câu lạc bộ.
Phần III. Trắc nghiệm trả lời ngắn
Cho hai tập hợp \(A = \left( {1;5} \right),B\left( {m;m + 1} \right)\). Tất cả các số thực m để B\A = có dạng [a; b]. Tính \(4a - b\).
Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi đúng hai môn Toán và Lý, 4 học sinh giỏi đúng hai môn Toán và Hóa, 2 học sinh giỏi đúng hai môn Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là bao nhiêu em?
Cho tập hợp \(B = \left\{ {x \in \mathbb{Z}|\left| {{x^2} + 1} \right| \le 2} \right\}\). Tập hợp B có bao nhiêu tập hợp con gồm 2 phần tử?
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}\,} \right|\,\,4 \le x \le 9} \right\}\) được kết quả là
\(\left[ {4\,;9} \right]\).
\(\left( {4\,;9} \right]\).
\(\left[ {4\,;9} \right)\).
\(\left( {4\,;9} \right)\).
Cho \(A = \left( {2\,;\; + \infty } \right)\) và \(B = \left( {m\,;\; + \infty } \right)\). Điều kiện cần và đủ của \(m\) để \(B \subset A\) là
\(m \ge 2\).
\(m \le 2\).
\(m = 2\).
\(m > 2\).
Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp \(A = \left( {1;11} \right]\)?
A. ![Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp \(A = \left( {1;11} \right]\)? A. B. C. D. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/8-1758594658.png)
![Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp \(A = \left( {1;11} \right]\)? A. B. C. D. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1758594667.png)
C.![Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp \(A = \left( {1;11} \right]\)? A. B. C. D. (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/09/7-1758594564.png)
![Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp \(A = \left( {1;11} \right]\)? A. B. C. D. (ảnh 5)](https://video.vietjack.com/upload2/quiz_source1/2025/09/10-1758594679.png)
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp
\(A = \left[ {7;11} \right].\)
\(A = \left( {7;11} \right].\)
\(A = \left[ {7;11} \right).\)
\(A = \left( {7;11} \right).\)
Hình nào sau đây minh họa tập \(A\) là con của tập \(B\)?
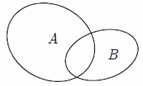
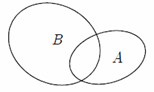
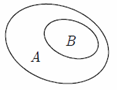
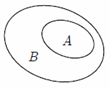
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho tập hợp \(X = \left\{ { - 3; - 1;0;1;3} \right\}\). Khi đó:
a)−1 là một phần tử của tập hợp X.
b) Số tập hợp con của X có 2 phần tử là 10.
c) Tập hợp X có thể cho bằng cách mô tả tính chất đặc trưng là \(X = \left\{ {x \in \mathbb{N}|x\left( {{x^2} - 9} \right)\left( {{x^2} - 1} \right) = 0} \right\}\).
d) Số tập con của tập hợp X có tối đa 3 phần tử là 26 tập hợp.
Cho tập hợp \(A = \left\{ {x + 1|x \in \mathbb{N},x \le 3} \right\}\). Khi đó:
a) 3 A.
b) Số phần tử của tập A là 5.
c) Số tập con của A chứa số 1 là 6.
d) Số tập con của A gồm có 3 phần tử là 2.
Cho tập hợp \(A = \left\{ {n \in \mathbb{N}|n \vdots 4,n < 2021} \right\}\).
a) Tập A gồm các phần tử là những số tự nhiên nhỏ hơn hoặc bằng 2020 và chia hết cho 4.
b) Khi sắp xếp các phần tử của tập hợp A theo thứ tự tăng dần thì hiệu của 2 phần tử liên tiếp là 4 đơn vị.
c) Tập hợp A có số phần tử là 505.
d) Tổng các phần tử của tập hợp A là S = 511060.
Phần III. Trắc nghiệm trả lời ngắn
Cho tập hợp \(A = \left\{ {2{k^2} + 3|k \in \mathbb{Z},\left| k \right| \le 3} \right\}\). Có bao nhiêu tập con của \(A\) chứa 3 phần tử?
Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}|{x^3} - x = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{Z}|\left| x \right| \le 2} \right\}\). Hỏi có bao nhiêu tập X thỏa mãn \(A \subset X \subset B\)?
Cho tập hợp \(B = \left\{ {x \in \mathbb{Z}|\left| {{x^2} + 1} \right| \le 2} \right\}\). Tập hợp B có bao nhiêu tập hợp con gồm 2 phần tử?








