Đề cương ôn tập giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Bài 1: Bất phương trình bậc nhất hai ẩn
34 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Cặp số \(\left( {x\,;y} \right)\) nào sau đây là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y > - 3}\\{ - x + 2y < 3}\end{array}} \right.\)?
\(\left( {1\,;0} \right)\).
\(\left( { - 5\,;0} \right)\).
\(\left( { - 2\,;3} \right)\).
\(\left( {0\,; - 5} \right)\).
Cặp số \(\left( {x\,;y} \right)\) nào sau đây không là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 3}\\{x - 2y > - 2}\end{array}} \right.\)?
\(\left( {0\,;0} \right)\).
\(\left( {1\,;1} \right)\).
\(\left( { - 1\,;1} \right)\).
\(\left( { - 1\,;0} \right)\).
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 > 0\end{array} \right.\]. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
\(N\left( { - 1\,;1} \right)\).
\(Q\left( { - 1\,;0} \right)\).
\(P\left( {1\,; - 3} \right)\).
\(M\left( {0\,;1} \right)\).
Miền không bị gạch chéo (kể cả các đường thẳng) là miền nghiệm của hệ bất phương trình nào?
\(\left\{ \begin{array}{l}x + y - 1 \ge 0\\2x - y + 4 \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y - 1 \ge 0\\2x - y + 4 \ge 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y - 1 \le 0\\2x - y + 4 \ge 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y - 1 \le 0\\2x - y + 4 \le 0\end{array} \right.\).
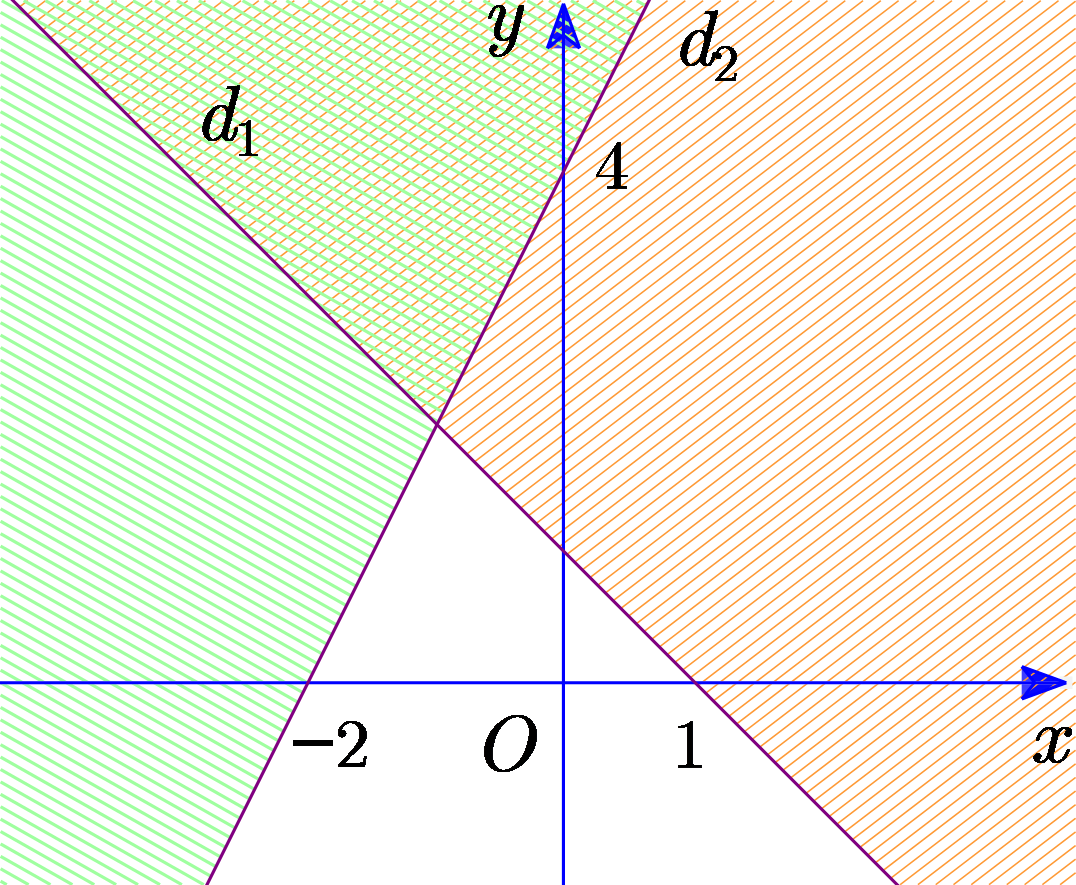
Trong hình vẽ dưới, phần mặt phẳng không bị gạch sọc (kể cả biên) là miền nghiệm của hệ bất phương trình nào dưới đây?
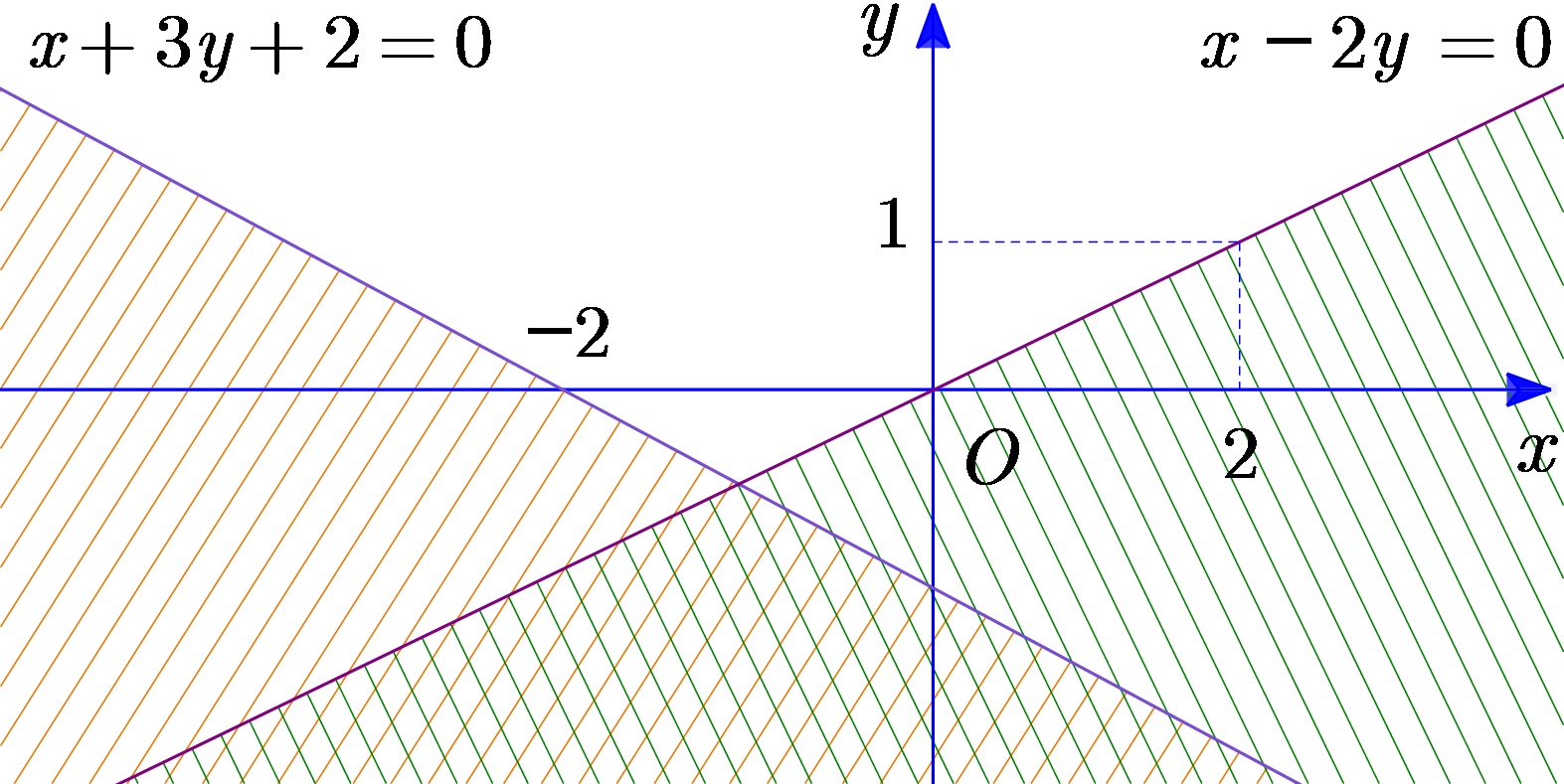
\(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y \ge 0\\x + 3y \ge - 2\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y \ge 0\\x + 3y \le - 2\end{array} \right.\).
Phần không gạch chéo ở hình sau đây (kể cả biên) là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn đáp án \[A\,,\,\,B\,,\,\,C\,,\,\,D\]?
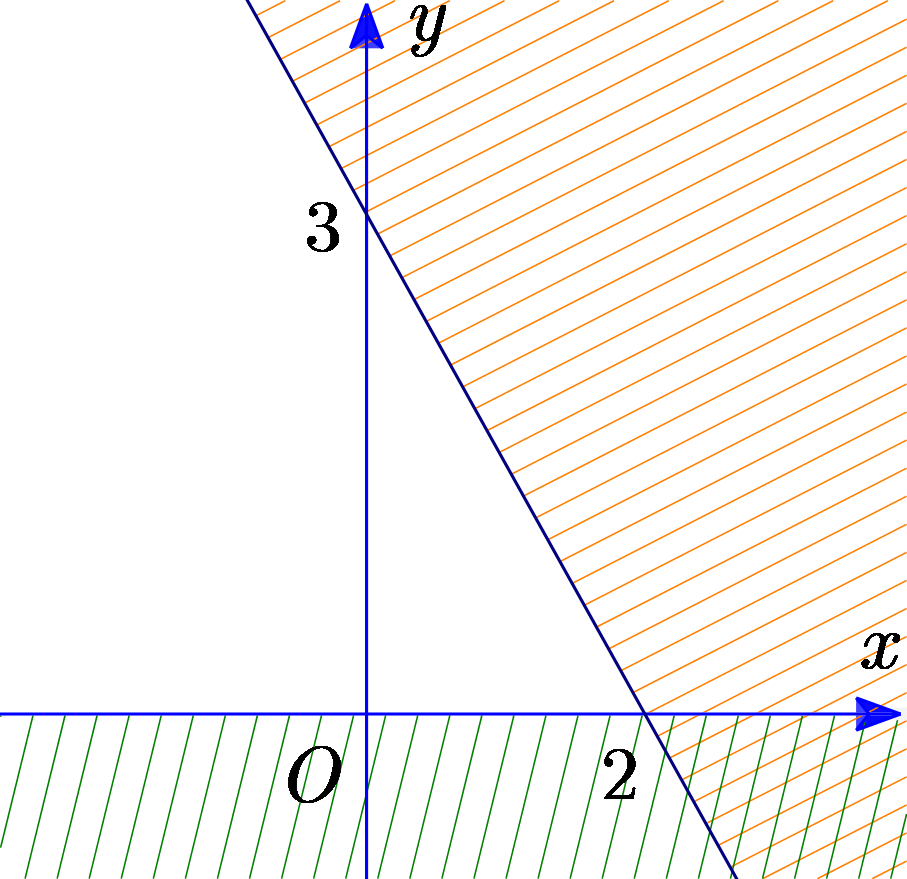
\(\left\{ \begin{array}{l}y \ge 0\\3x + 2y < - 6\end{array} \right.\).
\(\left\{ \begin{array}{l}x > 0\\3x + 2y < 6\end{array} \right.\).
\(\left\{ \begin{array}{l}y \ge 0\\3x + 2y \le 6\end{array} \right.\).
\(\left\{ \begin{array}{l}x \ge 0\\3x + 2y \ge - 6\end{array} \right.\).
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - y - 6 < 0\\x + 3y - 5 > 0\\x - 1 > 0\end{array} \right.\).
\(A\left( {0;7} \right)\).
\(B\left( {2;3} \right)\).
\(C\left( {2; - 3} \right)\).
\(Q\left( { - 1;2} \right)\).
Trong hình vẽ sau, miền được tô màu biểu diễn miền nghiệm của hệ bất phương trình nào?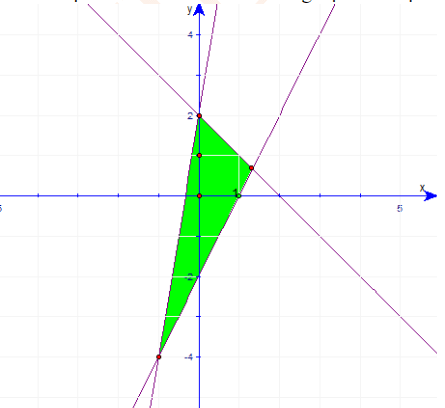
\(\left\{ \begin{array}{l}2x - y - 2 < 0\\x + y < 2\\6x - y + 2 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}2x - y - 2 < 0\\x + y < 2\\6x - y + 2 < 0\end{array} \right.\).
\(\left\{ \begin{array}{l}2x - y - 2 > 0\\x + 2y < 2\\6x - y + 2 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}2x - y - 2 > 0\\x + y > 2\\x - y + 2 > 0\end{array} \right.\).
Mỗi ngày bạn Thảo đều dành không quá 30 phút để đọc hai cuốn sách \(A\) và \(B\). Trung bình Thảo đọc được 3 trang sách \(A\) trong 2 phút và đọc được 2 trang sách \(B\) trong 1 phút. Gọi \(x\) và \(y\) lần lượt là số phút Thảo dùng để đọc sách \(A\) và sách \(B\)\[\left( {x\,,\,\,y \in \mathbb{N}} \right)\]. Tìm điều kiện cần và đủ của \(x\) và \(y\) để Thảo đọc được ít nhất 35 trang sách mỗi ngày.
\[\left\{ \begin{array}{l}3x + 4y \ge 70\\x + y \le 30\end{array} \right.\].
\[\left\{ \begin{array}{l}3x + 2y \ge 35\\x + y \le 30\end{array} \right.\].
\[3x + 4y \ge 70\].
\(3x + 2y \ge 35\).
Biết rằng hệ bất phương trình \(\left\{ \begin{array}{l} - x - 2y \ge - 10\\2x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) có miền nghiệm là một đa giác không bị gạch chéo như hình vẽ bên dưới:
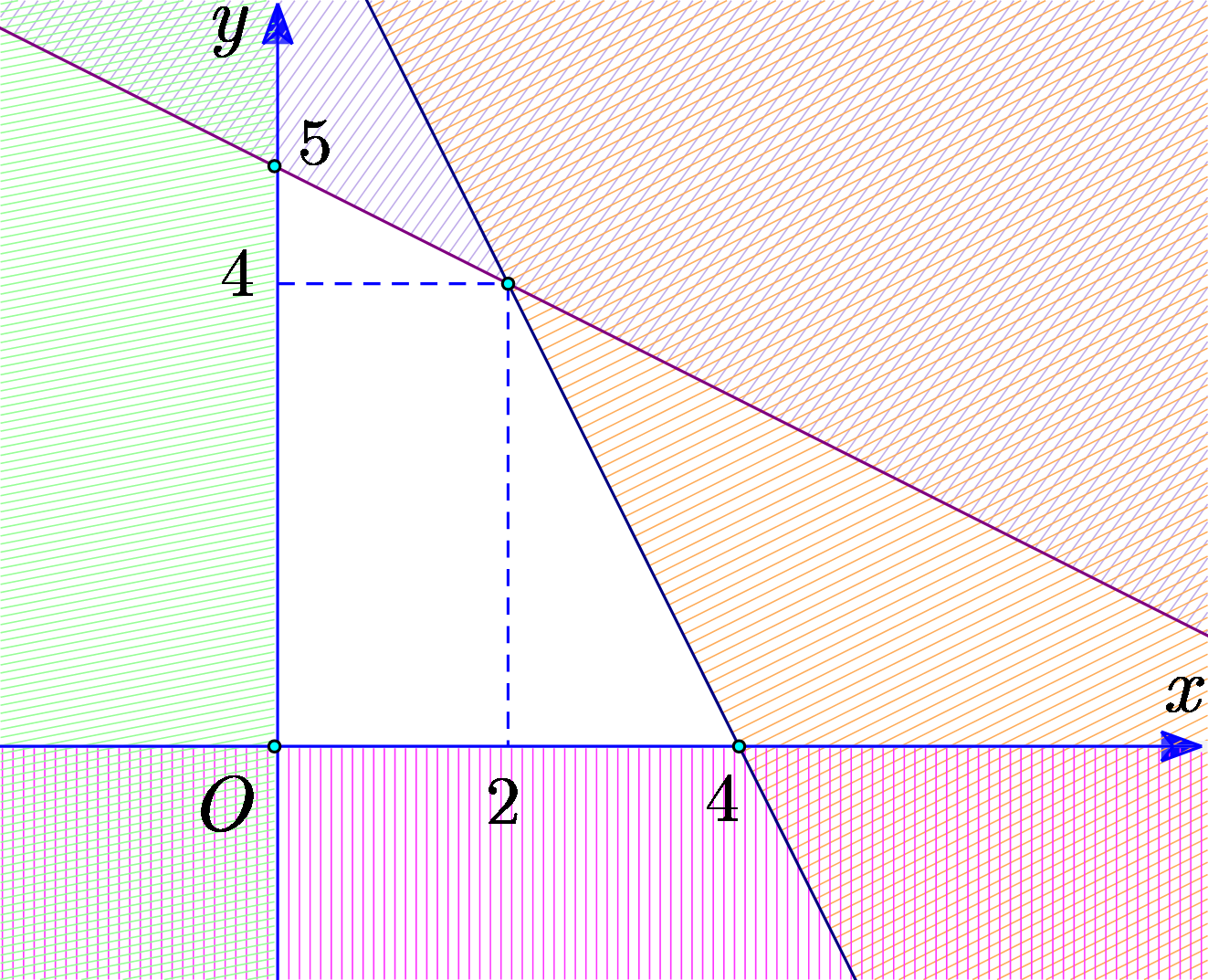
Giá trị lớn nhất của biểu thức \[F\left( {x\,;y} \right) = 3x - 2y + 1\] với \[\left( {x\,;y} \right)\] thỏa mãn hệ bất phương trình đã cho ở trên bằng
31.
\[ - 1\].
1.
13.
Biết rằng miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y - 100 \le 0}\\{2x + y - 80 \le 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\) là một đa giác được cho như hình vẽ bên dưới (phần không gạch sọc). Diện tích đa giác đó bằng
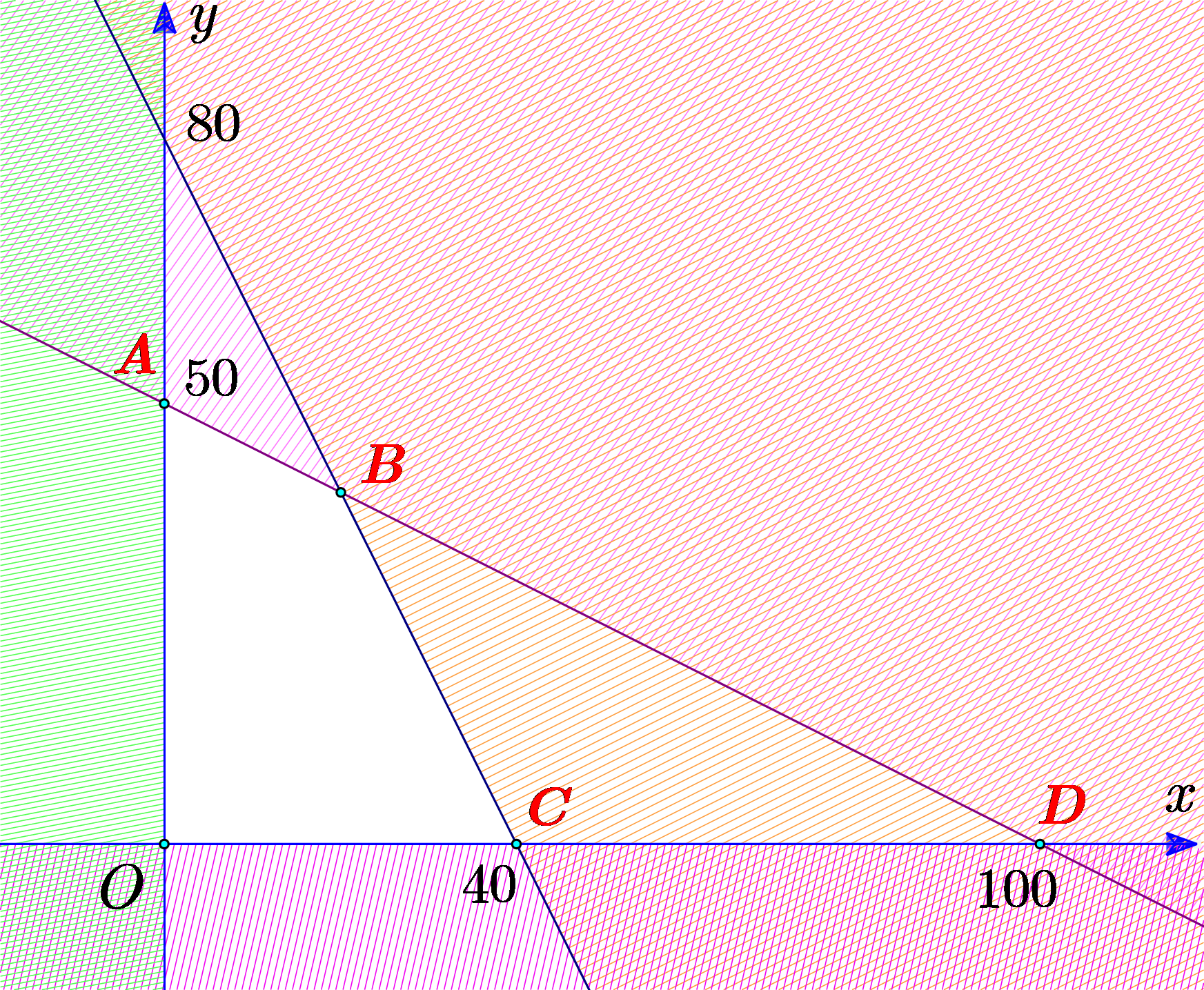
\[1200\].
\[1300\].
\[1100\].
\[1400\].
Biểu thức \(F\left( {x\,;y} \right) = 3x - y\) đạt giá trị nhỏ nhất bằng bao nhiêu trên miền nghiệm đa giác không gạch chéo trong hình vẽ bên dưới?
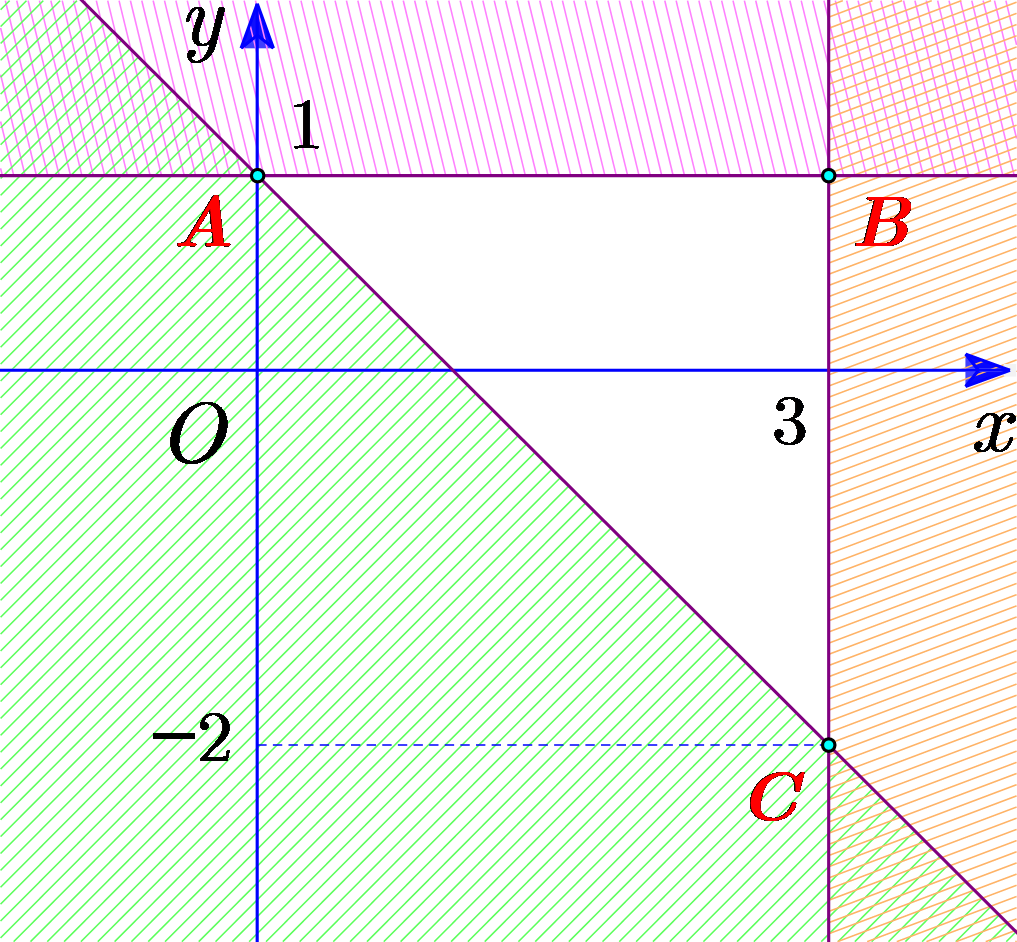
\(11\).
\( - 1\).
\( - 5\).
\(8\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\) (I).
a) \(\left( {0;3} \right)\) là một nghiệm của (I).
b) Miền nghiệm của (I) chứa điểm (1; 3).
c)\(M\left( {x;y} \right)\) thuộc miền nghiệm của (I) thì \(2y - x \le 7\).
d) Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định là 1.
Một công ty trong một đợt quảng cáo và bán hàng khuyến mại hàng hóa cho một sản phẩm mới của công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe lại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng; xe B chở tối đa 10 người và 1,5 tấn hàng. Gọi \(x,y\) lần lượt là số xe loại A và loại B mà công ty thuê.
a) Số tiền thuê xe là \(4x + 3y\).
b) \(2x + y < 14\).
c) \(2x + 5y \ge 30\).
d) Số tiền thuê xe thấp nhất là 32 triệu.
Một hộ nông dân định trồng ngô và khoai lang trên diện tích 4 ha. Trên diện tích mỗi ha, nếu trồng ngô thì cần 10 công và thu 2 triệu đồng, nếu trồng khoai lang thì cần 15 công và thu 2,5 triệu đồng. Biết tổng số công không quá 45 công. Gọi \(x;y\) lần lượt là số ha trồng ngô và khoai lang của hộ nông dân đó.
a) Tổng số công cần sử dụng là \(15x + 10y\).
b) Tổng số tiền thu được là \(F\left( {x;y} \right) = 2x + 2,5y\) triệu đồng.
c) Theo bài ra ta có hệ phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 4\\10x + 15y \le 45\end{array} \right.\).
d) Hộ nông dân đó thu được số tiền nhiều nhất là 8 triệu đồng.
Phần III. Trắc nghiệm trả lời ngắn
Cho biểu thức \(T = 3x - 2y - 4\) với \(x\) và \(y\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x - y - 1 \le 0\\x + 4y + 9 \ge 0\\x - 2y + 3 \ge 0\end{array} \right.\). Biết T đạt giá trị nhỏ nhất khi \(x = {x_0}\) và \(y = {y_0}\). Tính \(x_0^2 + y_0^2\).
Một xí nghiệp sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm I lãi 2 triệu đồng, một tấn sản phẩm II lãi 1,6 triệu đồng. Muốn sản xuất 1 tấn sản phẩm I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất 1 tấn sản phẩm II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 chỉ làm việc một ngày không quá 4 giờ. Gọi \(x\) là số tấn sản phẩm I sản xuất trong một ngày, \(y\) là số tấn sản phẩm II sản xuất trong một ngày. Tìm giá trị lớn nhất của \(L = 2x + 1,6y\).
Một trang trại cần thuê xe để vận chuyển một lúc 120 con bò sữa và 30 tấn thức ăn cho bò. Nơi cho thuê xẻ chỉ có 9 chiếc xe lớn và 10 chiếc xe nhỏ. Một chiếc xe lớn chỉ có thể chở được 15 con bò và 5 tấn thức ăn. Một chiếc xe nhỏ chỉ có thể chở 12 con bò và 2 tấn thức ăn. Giá thuê của một chiếc xe lớn là 500 nghìn đồng và một chiệc xe nhỏ là 350 nghìn đồng. Hỏi chủ trang trại cần thuê xe với chi phí thấp nhất là bao nhiêu nghìn đồng?
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Trong các cặp số \(\left( {x\,;y} \right)\) sau đây, cặp nào là nghiệm của bất phương trình \[2x + y < 1\]?
\[\left( { - 2\,;1} \right)\].
\[\left( {0\,;1} \right)\].
\[\left( {3\,;7} \right)\].
\[\left( {2\,; - 1} \right)\].
Cặp số \[\left( {3\,;2} \right)\] không là nghiệm của bất phương trình nào sau đây?
\[x + 3y + 1 < 0\].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(2{x^2} + 3{y^2} < 0\).
\(2xy - y > 0\).
\(2x + 3{y^2} > 0\).
\(2x + 3y < 0\).
Miền nghiệm của bất phương trình \[3x + 2\left( {y - 3} \right) \ge 4\left( {x - 2} \right) - y - 1\] là nửa mặt phẳng chứa điểm nào sau đây?
\[\left( {2\,; - 2} \right)\].
\[\left( { - 3\,;1} \right)\].
\[\left( {4\,;0} \right)\].
\[\left( {0\,; - 2} \right)\].
Miền nghiệm của bất phương trình \(3x - 2y \ge - 6\) được biểu diễn bởi phần không gạch chéo trong hình nào được cho dưới đây ?
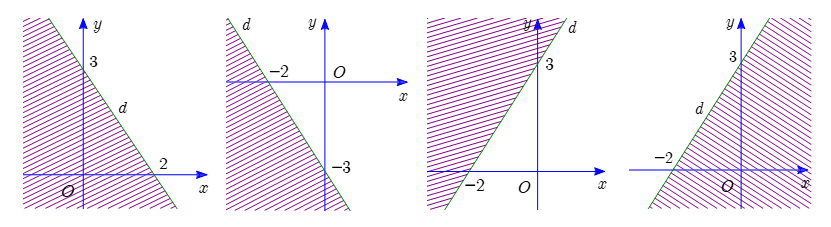
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Miền không bị gạch (không tính đường thẳng) được cho bởi hình sau là miền nghiệm của bất phương trình nào?

\[2x + y - 6 > 0\].
\[2x + y - 6 < 0\].
\[x + 2y - 6 < 0\].
\[x + 2y - 6 > 0\].
Phần không bị gạch (kể cả bờ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
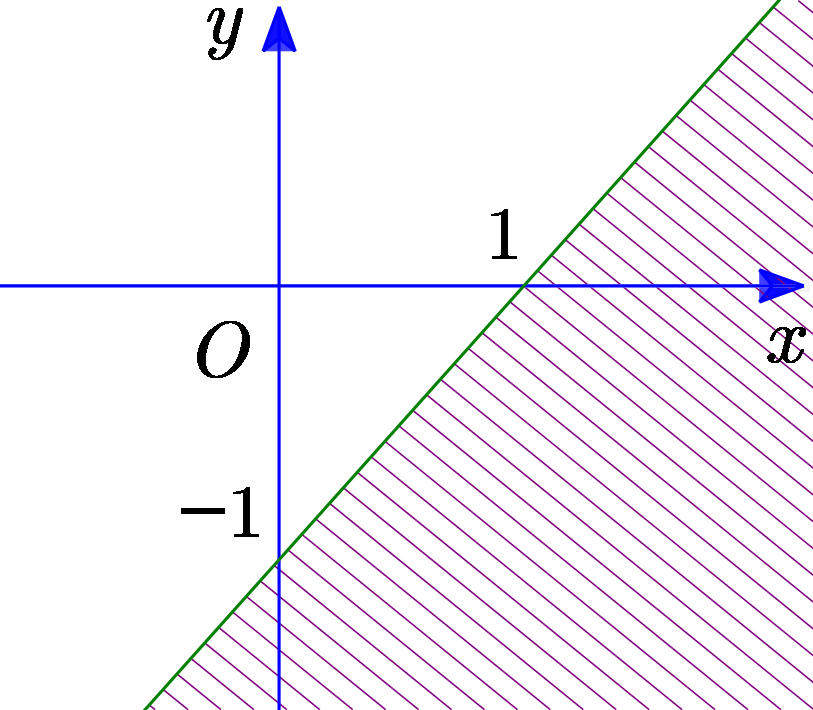
\(x + y > 1\).
\(x - y < 1\).
\(x + y \le 1\).
\(x - y \le 1\).
Bất phương trình nào sau đây có miền nghiệm được biểu diễn bởi phần không gạch sọc (tính cả biên) trong hình vẽ bên dưới?
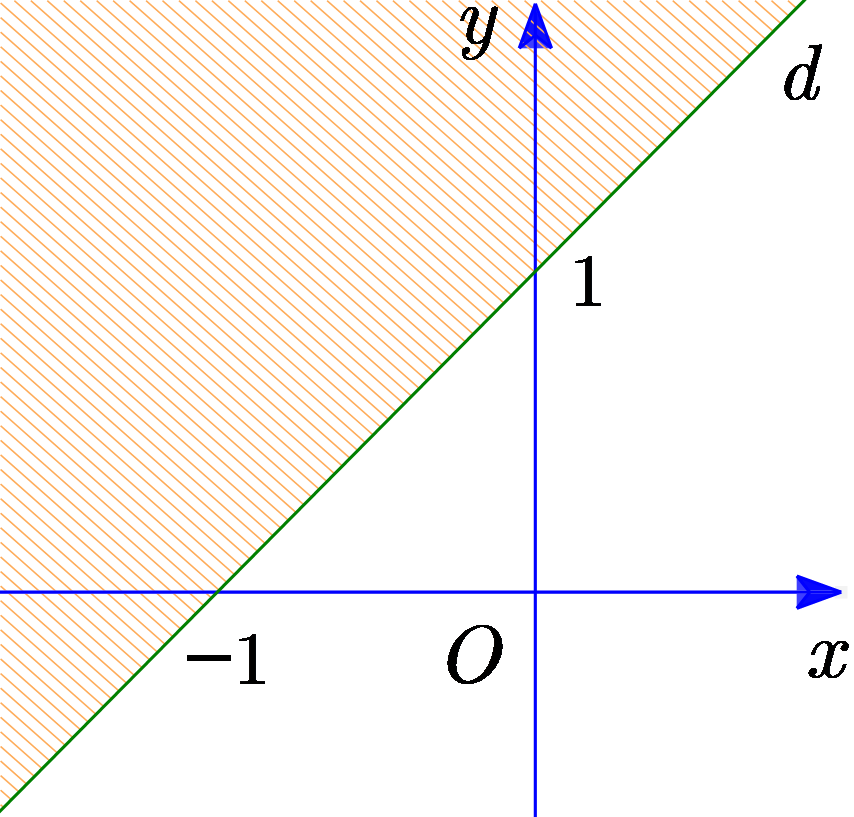
\(2x - y + 1 \le 0\).
\(2x - y + 1 > 0\).
\(x - y + 1 \ge 0\).
\(x - y + 1 < 0\).
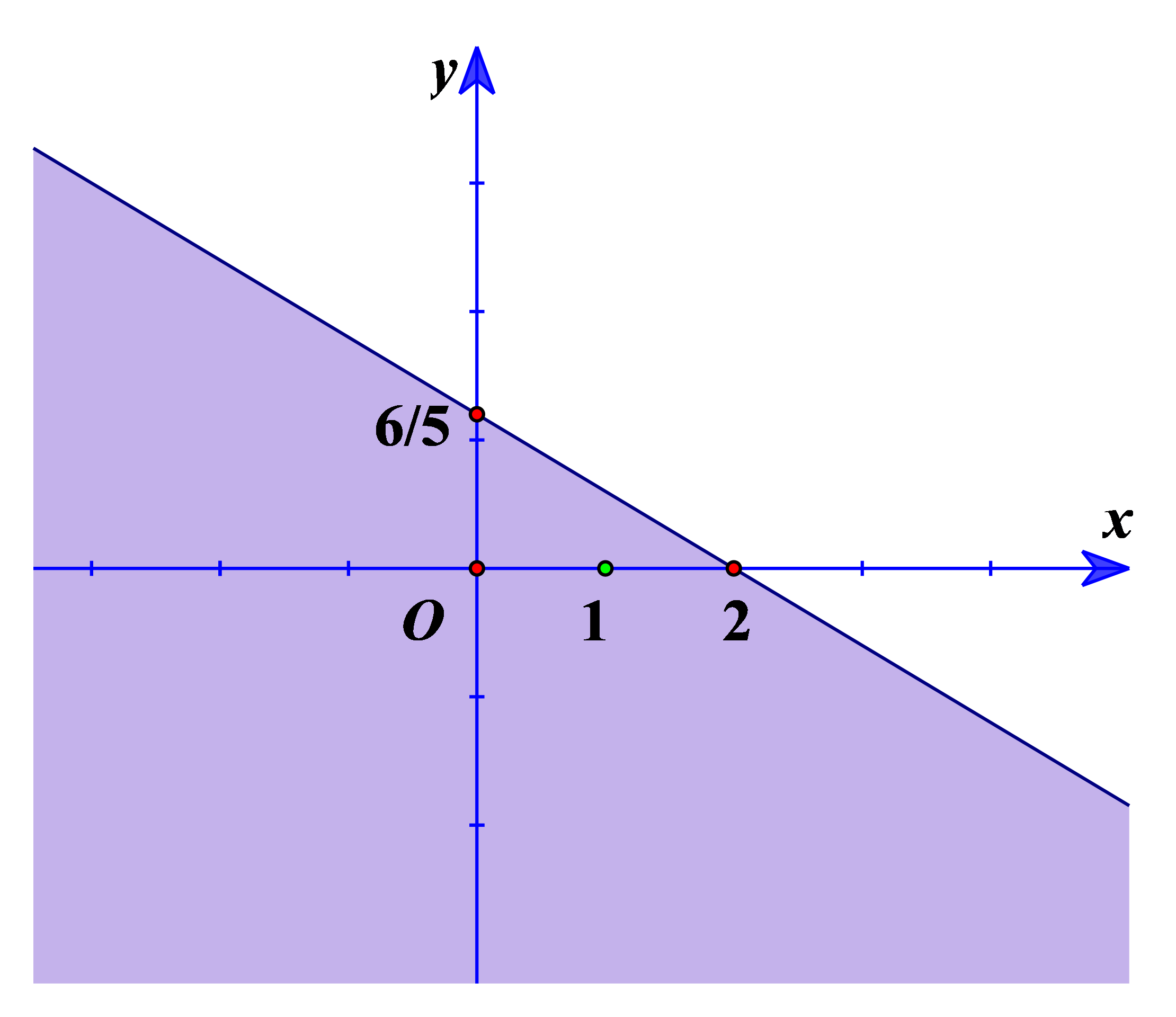
Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
![Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây? A. \[x + 2y < 4\]. B. \[2x + y \ge 4\]. C. \[x + 2y \ge 4\]. D. \[x + 2y > 4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1758596000.png)
\[x + 2y < 4\].
\[2x + y \ge 4\].
\[x + 2y \ge 4\].
\[x + 2y > 4\].
Bạn Việt mang \(100\,000\) đồng ra chợ mua hoa cúc và hoa hồng. Một bông hoa cúc có giá \(3\,000\) đồng, một bông hoa hồng có giá \(6\,000\) đồng. Gọi \(x\) và \(y\) lần lượt là số bông hoa cúc và số bông hoa hồng bạn Việt mua. Bất phương trình bậc nhất hai ẩn \(x,\,\,y\) để biểu diễn số tiền Việt mua hoa cúc và hoa hồng là
\(3x + 6y \le 100\).
\(6x + 3y \le 100\).
\(3x + 6y \ge 100\).
\(6x + 3y \ge 100\).
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho bất phương trình \(2x + 5y > 5\) (1).
a) Bất phương trình (1) là bất phương trình bậc nhất hai ẩn.
b) Cặp số \(\left( {x;y} \right) = \left( {1;1} \right)\) thuộc miền nghiệm của bất phương trình (1).
c) Bất phương trình (1) có một nghiệm duy nhất.
d) Miền nghiệm không được tô đậm (không kể bờ d) trong hình sau là miền nghiệm của bất phương trình (1).
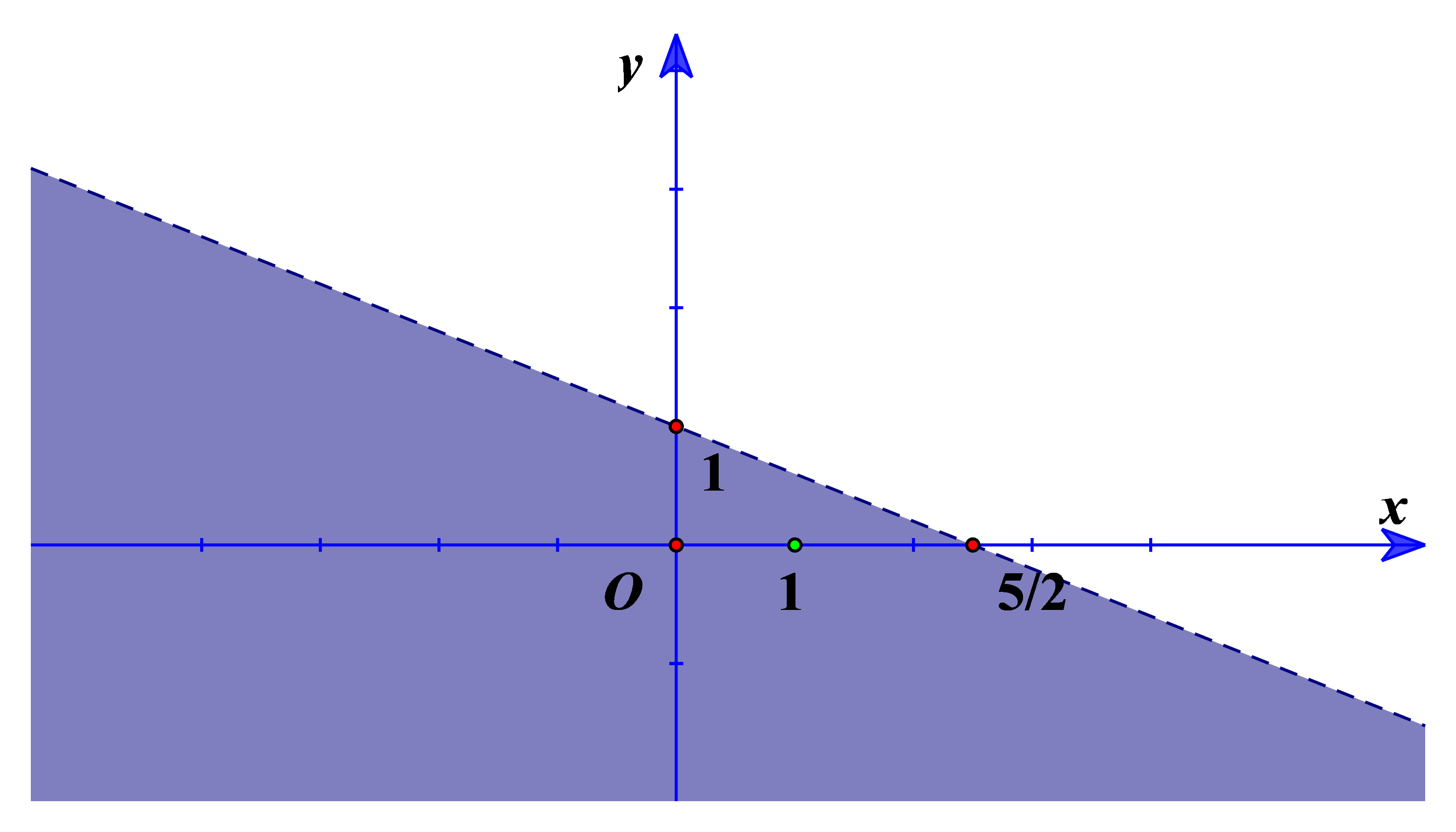
Cho bất phương trình bậc nhất hai ẩn \(3x + 5y \le 6\).
a) Cặp (3; 3) là một nghiệm của bất phương trình.
b) Điểm \(B\left( { - 2;2} \right)\) thuộc miền nghiệm của bất phương trình đã cho.
c) Với \(x = 0\) thì chỉ có 2 giá trị của y thỏa mãn bất phương trình.
d) Miền nghiệm của bất phương trình đã cho là miền tô đậm trong hình vẽ bao gồm cả bờ là đường thẳng \(3x + 5y = 6\).
Nhân ngày tết trung thu, một rạp chiếu phim phục vụ khán giả một bộ phim hoạt hình. Vé bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6 – 13 tuổi): 50000 đồng/vé.
Loại 2 (dành cho người trên 13 tuổi): 100000 đồng/vé.
Người ta tính toán rằng nếu bán được \(x\) vé loại 1 và \(y\) vé loại 2, để không phải bù lỗ thì số tiền vé thu được phải đạt tối thiểu 20 triệu đồng.
a) Số tiền bán được của vé loại 1 là \(50000x\), số tiền bán được của vé loại 2 là \(100000y\) với điều kiện \(x \ge 0;y \ge 0\).
b) Bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) để rạp phim không bị lỗ là \(50x + 100y \le 20000\).
c) \(\left( {200;100} \right)\) là một nghiệm của bất phương trình bậc nhất \(50x + 100y \ge 20000\).
d) Miền nghiệm của bất phương trình \(50x + 100y \ge 20000\) là nửa mặt phẳng bờ là đường thẳng \(d:50x + 100y = 20000\) không chứa điểm \(O\left( {0;0} \right)\).
Phần III. Trắc nghiệm trả lời ngắn
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn [−2022; 2022] để điểm (1; 1) không thuộc miền nghiệm của bất phương trình \(x + \left( {m + 1} \right)y + 1 \ge 0\).
Vào dịp Tết Nguyên đán nhà trường tổ chức Cuộc thi gói bánh chưng và bánh tày thể lệ như sau: Mỗi đội chơi được sử dụng tối đa 240000 đồng để mua nguyên liệu. Các bạn trong đội thi lớp 10A tính toán và thấy rằng để gói một cái bánh chưng mua hết 40000 đồng nguyên liệu và để gói một cái bánh tày mua hết 30000 đồng nguyên liệu. Gọi \(x;y\left( {x,y \in \mathbb{N}} \right)\)lần lượt là số bánh chưng và số bánh tày lớp 10A gói. Khi đó \(x\) và \(y\) thỏa mãn bất phương trình \(ax + 6y \le b\). Tính giá trị biểu thức \(3a - 2b\).
Trong mặt phẳng Oxy, phần nửa mặt phẳng không tô đậm (kể cả bờ) trong hình vẽ dưới đây là biểu diễn hình học tập nghiệm của bất phương trình \(ax + by \le 3\). Tính giá trị \(2a + b\).