Bộ 5 đề thi giữa kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới (Đề số 5)
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Rút gọn biểu thức \(P = {x^{\frac{1}{3}}}.\sqrt[6]{x}\) với \(x > 0\).
\(P = \sqrt x \).
\(P = {x^{\frac{1}{3}}}\).
\(P = {x^{\frac{1}{9}}}\).
\(P = {x^2}\).
Với \(a,b,x\) là các số thực dương thỏa mãn \({\log _2}x = 5{\log _2}a + 3{\log _2}b\), mệnh đề nào dưới đây đúng?
\(x = 3a + 5b\).
\(x = 5a + 3b\).
\(x = {a^5} + {b^3}\).
\(x = {a^5}{b^3}\).
Trong các hàm số sau, hàm số nào sau đây là hàm số mũ?
\(y = {x^2}\).
\(y = {2^x}\).
\(y = {x^\pi }\).
\(y = \sqrt x \).
Tập nghiệm \(S\) của bất phương trình \({\log _2}x > 2\) là:
\(S = \left( {2; + \infty } \right)\).
\(S = \left( {0;2} \right)\).
\(S = \left( {0;4} \right)\).
\(S = \left( {4; + \infty } \right)\).
Giá trị của biểu thức \(A = \frac{{{6^{3 + \sqrt 5 }}}}{{{2^{2 + \sqrt 5 }}{{.3}^{1 + \sqrt 5 }}}}\) bằng
\({6^{ - \sqrt 5 }}\).
\(18\).
\(1\).
\(9\).
Tìm \(a\) để hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình bên
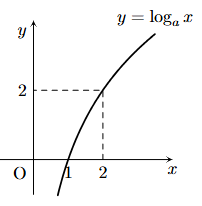
\(a = \sqrt 2 \).
\(a = \frac{1}{{\sqrt 2 }}\).
\(a = \frac{1}{2}\).
\(a = 2\).
Mệnh đề nào sau đây là đúng?
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Hai đường thẳng cùng vuông góc gới một đường thẳng thì song song với nhau.
Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
Trong không gian mặt phẳng \(\left( P \right)\) và đường thẳng \(d\) không vuông góc với mặt phẳng \(\left( P \right)\). Hãy chọn mệnh đề phát biểu đúng trong các mệnh đề dưới đây?
Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
Không tồn tại mặt phẳng \(\left( \alpha \right)\)chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) vuông góc với \(\left( P \right)\).
Tồn tại duy nhất một đường thẳng \(\Delta \) nằm trên mặt phẳng \(\left( P \right)\) và \(\Delta \) vuông góc với \(d\).
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không vuông góc với nhau. Gọi \(a'\) là hình chiếu vuông góc của \(a\) lên mặt phẳng \(\left( P \right)\). Giả sử \(b\) là một đường thẳng nằm trong mặt phẳng \(\left( P \right)\) và \(b \bot a'\).
Khi đó
Đường thẳng \(a\) luôn luôn chéo \(b\).
Đường thẳng \(a\) luôn luôn cắt \(b\).
\(a//b\).
\(a \bot b\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), đáy \(ABC\) là tam giác vuông tại \(A\), \(M\) là trung điểm \(BC\). Khi đó mặt phẳng \(\left( {ABC} \right)\) không vuông góc với mặt phẳng nào?
\(\left( {SAB} \right)\).
\(\left( {SAM} \right)\).
\(\left( {SAC} \right)\).
\(\left( {SBC} \right)\).
Hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) được gọi là vuông góc với nhau nếu:
góc giữa chúng bằng \(90^\circ \).
góc giữa chúng bằng \(180^\circ \).
góc giữa chúng bằng \(0^\circ \).
góc giữa chúng bằng \(45^\circ \).
Cho hình chóp đều \(S.ABCD\). Gọi \(I\) là trung điểm của \(AB\), \(G\) là trọng tâm của tam giác \(SCD\). Trong các mệnh đề sau, mệnh đề nào đúng?
\(\left( {SAC} \right) \bot \left( {SAD} \right)\).
\(\left( {SAB} \right) \bot \left( {SIG} \right)\).
\(\left( {SIG} \right) \bot \left( {SBC} \right)\).
\(\left( {SAD} \right) \bot \left( {SBD} \right)\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình \({9^{2x}}{.27^{{x^2}}} = \frac{1}{3}\).
a) \(x = 0\) là một nghiệm của phương trình.
b) \(x = - 1\)không phải là nghiệm của phương trình.
c) Tổng các nghiệm của phương trình là \(0\).
d) \(x_1^2 + x_2^2 = \frac{{10}}{9}\) với \({x_1},{x_2}\) là hai nghiệm của phương trình trên.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và tam giác \(ABC\) vuông tại \(B\). Gọi \(H,K\) là hình chiếu vuông góc của \(A\) trên các cạnh \(SB,SC\). Khi đó:
a) \(SA \bot BC\).
b) Tam giác \(SBC\) cân tại \(B\).
c) \(AH\) vuông góc với mặt phẳng \(\left( {SBC} \right)\).
d) Giả sử \(HK\) cắt \(BC\) tại \(D\). Khi đó \(\left( {AC,AD} \right) = 90^\circ \).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18.
Anh Toàn được tuyển dụng vào một công ty đầu năm 2013. Công ty trả lương cho anh theo nguyên tắc. Lương khởi điểm anh nhận là 6 triệu đồng/tháng và cứ sau 3 năm công ty lại tăng lương cho anh thêm 25% số lương đang hưởng. Hiện nay (năm 2024) anh đang được hưởng lương là bao nhiêu triệu đồng một tháng? (kết quả làm tròn đến hàng phần mười).
Cho \(a\) là số thực dương \(a \ne 1\). Tính \(P = {\log _{\sqrt[3]{a}}}{a^3}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, tam giác \(SAD\) là tam giác đều. Góc giữa hai đường thẳng \(BC\) và \(SA\) bằng bao nhiêu độ?
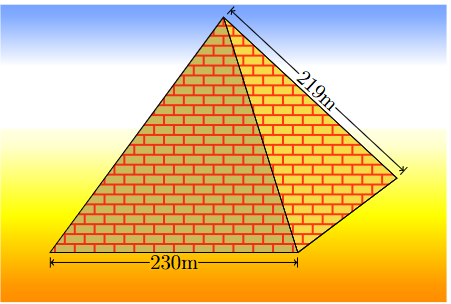
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có độ dài cạnh đáy khoảng 230m, các cạnh bên bằng nhau và dài khoảng 219 m. Gọi \(\varphi \) là số đo của góc tạo bởi mặt bên và mặt đáy của kim tự tháp. Tính \(\tan \varphi \) (tính chính xác đến hàng phần trăm).
PHẦN II. TỰ LUẬN
Rút gọn biểu thức \(P = {\log _3}\left( {{x^3} + x} \right) - {\log _3}\left( {{x^2} + 1} \right)\) với \(x > 0\).
Lốc xoáy là hiện tượng một luồng không khí xoáy tròn mở rộng ra từ một đám mây dông xuống tới mặt đất. Các cơn lốc xoáy thường có sức tàn phá rất lớn. Tốc độ của gió (đơn vị: dặm/giờ) gần tâm của một cơn lốc xoáy được tính bởi công thức \(S = k.\log d + 65\) (Nguồn: Ron Larson, Intermediate Algebra, Cengage) trong đó \(d\)(đơn vị: dặm) là quãng đường cơn lốc xoáy di chuyển được. Biết tốc độ của gió ở gần tâm (làm tròn kết quả đến hàng đơn vị) khi cơn lốc xoáy di chuyển được quãng đường là 10 dặm là 158 (dặm/giờ). Hãy tính tốc độ của gió ở gần tâm (làm tròn kết quả đến hàng đơn vị) khi cơn lốc xoáy di chuyển được quãng đường là 12 dặm.
Một chiếc cột được dựng trên nền sân phẳng. Gọi \(O\) là điểm đặt chân cột trên mặt sân và \(M\) là điểm trên cột cách chân cột \(40\) cm. Trên mặt sân, người ta lấy hai điểm \(A\) và \(B\) đều cách \(O\) là \(30\) cm (\(A,B,O\) không thẳng hàng). Người ta đo độ dài \(MA\) và \(MB\) đều bằng 50 cm. Hỏi theo các số liệu trên, chiếc cột có vuông góc với mặt sân hay không?