Bộ 5 đề thi giữa kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới (Đề số 4)
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Với \(a\) là số thực dương tùy ý, tích \({a^2}.{a^{\frac{1}{2}}}\) bằng
\({a^{\frac{5}{2}}}\).
\(a\).
\({a^{\frac{3}{2}}}\).
\({a^{\frac{1}{4}}}\).
Đặt \(a = {\log _2}5\). Khi đó \({\log _{25}}32\) bằng
\(\frac{5}{{2a}}\).
\(\frac{{5a}}{2}\).
\(\frac{2}{{5a}}\).
\(\frac{{2a}}{5}\).
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
\(y = {\left( {\frac{1}{e}} \right)^x}\).
\(y = {\left( {\sqrt {\frac{1}{\pi }} } \right)^x}\).
\(y = {\left( {\frac{1}{3}} \right)^x}\).
\(y = {\left( {\sqrt[{2024}]{\pi }} \right)^x}\).
Tập nghiệm \(S\) của bất phương trình \(\log x < 1\) là
\(S = \left( { - \infty ;10} \right)\).
\(S = \left( {0;10} \right)\).
\(S = \left( {10; + \infty } \right)\).
\(S = \left( { - \infty ;1} \right)\).
Cho \({\log _a}b = 2\) với \(a,b\) là số thực dương và \(a\) khác 1. Tính giá trị biểu thức \(T = {\log _{{a^2}}}{b^6} + {\log _a}\sqrt b \).
\(T = 7\).
\(T = 6\).
\(T = 5\).
\(T = 8\).
Trong hình vẽ bên có đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\). Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
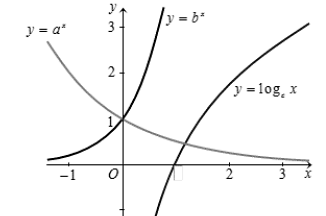
\(a < c < b\).
\(c < a < b\).
\(a < b = c\).
\(b < c < a\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Góc giữa hai đường thẳng \(SD\) và \(BC\) bằng
Góc giữa hai đường thẳng \(SD\) và \(DC\).
Góc giữa hai đường thẳng \(SD\) và \(AD\).
Góc giữa hai đường thẳng \(SD\) và \(BD\).
Góc giữa hai đường thẳng \(SD\) và \(SC\).
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình vuông tâm \(O\). Hình chiếu của điểm \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm
\(B\).
\(D\).
\(O\).
\(A\).
Cho hình chóp\(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Khẳng định nào dưới đây sai?
\(SA \bot AB\).
\(SA \bot BC\).
\(SA \bot AC\).
\(SB \bot AB\).
Cho các đường thẳng \(a,b\) và các mặt phẳng \(\left( \alpha \right),\left( \beta \right)\). Chọn mệnh đề đúng trong các mệnh đề sau
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\a \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \bot \left( \alpha \right)\end{array} \right. \Rightarrow b//\left( \alpha \right)\).
\(\left\{ \begin{array}{l}a \bot b\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
\(\left\{ \begin{array}{l}\left( \alpha \right) \bot \left( \beta \right)\\a \subset \left( \alpha \right)\\b \subset \left( \beta \right)\end{array} \right. \Rightarrow a \bot b\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\) và các cạnh bên bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm \(AD\) và \(SD\). Số đo góc \(\left( {MN,SC} \right)\) bằng
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
Cho tam giác \(ABC\) vuông cân tại \(B\) và \(AB = a\). Trên đường thẳng qua \(A\) vuông góc với \(\left( {ABC} \right)\) lấy điểm \(S\) sao cho \(SA = a\). Tính số đo góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\).
\(60^\circ \).
\(45^\circ \).
\(30^\circ \).
\(90^\circ \).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho \(a,b\) là hai số thực dương và biểu thức \(A = 3{\log _2}a + {\log _2}b\).
a) Nếu \(a = 4;b = 2\) thì \(A = 6\).
b) Biểu thức \(A = {\log _2}\left( {{a^3}b} \right)\).
c) Nếu \({a^3}b = 8\). Giá trị của biểu thức \(A\) bằng 3.
d) Nghiệm của phương trình \({\log _2}x = 2A\) là \(x = {a^3}{b^2}\).
Cho hình chóp đều \(S.ABC\) có \(ABC\) là tam giác đều cạnh \(a\), cạnh bên \(SA = \frac{{a\sqrt {21} }}{6}\). Gọi \(G\) là trọng tâm của \(\Delta ABC\) và kẻ \(AM \bot BC\).
a) Đường thẳng \(SG\) vuông góc với mặt phẳng \(\left( {ABC} \right)\).
b) \(SM \bot BC\).
c) Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) là góc \(\widehat {SMA}\).
d) Giá trị góc \(\alpha \) giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18.
Tập nghiệm \(S\) của bất phương trình \({5^{x + 2}} < {\left( {\frac{1}{{125}}} \right)^{ - x}}\) là \(\left( {a; + \infty } \right)\). Tìm \(a\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(AC\) và \(A'D\) bằng bao nhiêu độ?
Trong vật lí, sự phân rã các chất phóng xạ được cho bởi công thức \(m\left( t \right) = {m_0}{\left( {\frac{1}{2}} \right)^{\frac{t}{T}}}\). Trong đó, \({m_0}\) là khối lượng chất phóng xạ ban đầu (tại thời điểm \(t = 0\)), \(m\left( t \right)\) là khối lượng chất phóng xạ tại thời điểm \(t\) và \(T\) là chu kì bán rã. Hạt nhân Poloni (\({P_0}\)) là chất phóng xạ \(\alpha \)có chu kì bán rã 138 ngày. Giả sử lúc đầu có 100 Poloni. Tính khối lượng Poloni còn lại sau 100 ngày theo đơn vị gam (làm tròn kết quả đến phần chục).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Gọi \(H\) là trung điểm của \(AB\) và \(SH \bot \left( {ABCD} \right)\), gọi \(K\) là trung điểm của cạnh \(AD\). Góc giữa hai đường thẳng \(BK\) và \(SC\) bằng bao nhiêu độ?
PHẦN II. TỰ LUẬN
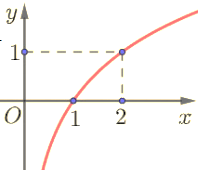
Cho các hàm số \(y = {\log _2}x;y = {\log _{\frac{1}{2}}}x;y = {\left( {\frac{1}{2}} \right)^x}\) và \(y = {2^x}\). Đồ thị hàm số dưới đây là của hàm số nào đã cho?
Một ngân hàng \(X\), quy định về số tiền nhận được của khách hàng sau \(n\) năm gửi tiền vào ngân hàng tuân theo công thức \(P\left( n \right) = A{\left( {1 + 8\% } \right)^n}\), trong đó \(A\) là số tiền gửi ban đầu của khách hàng. Hỏi số tiền ít nhất mà khách hàng phải gửi là bao nhiêu để sau 3 năm khách hàng đó nhận được lớn hơn 850 triệu đồng (kết quả làm tròn đến hàng triệu).
Kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc tạo bởi mặt bên và mặt đáy của kim tự tháp đó (đơn vị đo góc là độ, làm tròn đến hàng phần chục).