Bộ 5 đề thi giữa kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho a là một số thực dương, biểu thức \({a^{\frac{2}{3}}}\sqrt a \)viết dưới dạng lũy thừa với số mũ hữu tỉ là
\({a^{\frac{5}{6}}}\).
\({a^{\frac{7}{6}}}\).
\({a^{\frac{{11}}{6}}}\).
\({a^{\frac{6}{5}}}\).
Cho \(a > 0,\,a \ne 1\), biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu?
\( - 3\).
\(3\).
\(\frac{1}{3}\).
\( - \frac{1}{3}\).
Nghiệm của phương trình \({\log _2}x = 3\) là
\(9\).
\(6\).
\(8\).
\(\frac{3}{2}\).
Mệnh đề nào đúng trong các mệnh đề sau?
Góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Góc giữa hai đường thẳng là góc nhọn.
Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] khi \[b\] song song với \[c\] (hoặc \[b\] trùng với \[c\]).
Góc giữa hai đường thẳng \[a\] và \[b\] bằng góc giữa hai đường thẳng \[a\] và \[c\] thì \[b\] song song với \[c\].
Qua \(O\) cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng \(\Delta \) cho trước?
\(1\).
Vô số.
\(3\).
\(2\).
Mệnh đề nào sau đây là đúng?
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Cường độ một trận động đất M (richter) được cho bởi công thức \(M = \log A - \log {A_0}\), với \(A\) là biên độ rung chấn tối đa và \({A_0}\) là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ gần với số nào sau đây nhất là
\(8,9\).
\(7,9\).
\(8,6\).
\(8,4\).
Cho đồ thị hai hàm số \(y = {a^x}\) và \(y = {\log _b}x\) như hình vẽ
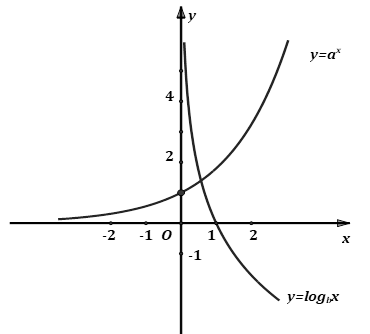
\(a > 1;b > 1\).
\(a > 1;0 < b < 1\).
\(0 < a < 1;0 < b < 1\).
\(0 < a < 1;b > 1\).
Nghiệm của phương trình \({\left( {\frac{1}{{25}}} \right)^{x + 1}} = {125^{2x}}\) là
\(x = 1\).
\(x = 4\).
\(x = - \frac{1}{4}\).
\(x = - \frac{1}{8}\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B,\) cạnh bên \(SA\) vuông góc với đáy. Gọi \(H\) là chân đường cao kẻ từ \(A\) của tam giác \(SAB\). Khẳng định nào dưới đây là sai?
\(SA \bot BC\).
\(AH \bot BC\).
\(AH \bot AC\).
\(AH \bot SC\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và đáy \(ABC\) là tam giác đều. Khẳng định nào sau đây sai?
\(\left( {SAB} \right) \bot \left( {ABC} \right)\).
Gọi \(H\) là trung điểm của cạnh \(BC\). Khi đó \(\widehat {AHS}\) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right).\)
Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAC} \right)\) là \(\widehat {ACB}\).
\(\left( {SAC} \right) \bot \left( {ABC} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, cạnh bên \(SA\) vuông góc với đáy. Tính diện tích hình chiếu của \(\Delta SBC\) trên mặt phẳng \(\left( {SAC} \right)\) biết \(SA = AB = 2a;AD = a\).
\({a^2}\sqrt 2 \).
\(\frac{{{a^2}\sqrt 5 }}{2}\).
\({a^2}\).
\(\frac{{{a^2}\sqrt 5 }}{5}\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho các đồ thị hàm số \(y = {\log _a}x;y = {\log _b}x;y = {\log _c}x\) như hình vẽ.
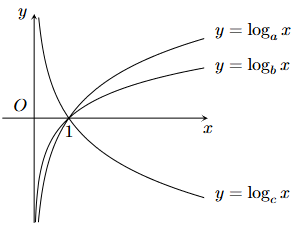
a) \(a > 1\).
b) \(0 < c < 1 < a < b\).
c) \({\left( {{a^3}.\sqrt a } \right)^{{{\log }_a}b}} = \sqrt[3]{{{b^2}}}\).
d) \(P = \log \frac{a}{b} + \log \frac{b}{c} + \log \frac{c}{d} - \log \frac{a}{d} > 0\) với \(d > 0\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\). Cạnh bên \(SA\) vuông góc với đáy. \(M\) là trung điểm của \(AC\).
a) \(SA \bot BC\).
b) \(\left( {SAB} \right) \bot \left( {ABC} \right)\).
c) \(BM \bot \left( {SAC} \right)\).
d) Mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {SAC} \right)\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 15 đến câu 18
Với \(a\) là số thực dương tùy ý, biểu thức \({a^{\frac{5}{3}}}.{a^{\frac{1}{3}}}\) được viết dưới dạng \({a^m}\). Tính \(m\).
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ dưới đây
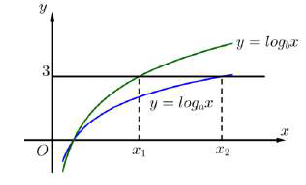
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},{x_2}\). Biết \({x_2} = 2{x_1}\). Tính \(\frac{{{a^3}}}{{{b^3}}}\).
Cho hình bình hành \(ABCD\) tâm \(O\) có bao nhiêu đường thẳng đi qua điểm \(O\) và vuông góc với mặt phẳng \(\left( {ABCD} \right)\)?
Kim tự tháp Giza cao nguyên Tượng đài Butte Hệ sinh thái Badlands có dạng hình chóp tứ giác đều. Giả sử cạnh đáy của kim tự tháp có chiều dài bằng 60 m và chiều cao của kim tự tháp bằng \(10\sqrt 3 \) m. Độ nghiêng của mặt bên kim tự tháp so với mặt đất là bao nhiêu độ? (xem mặt đất là mặt phẳng).
PHẦN II. TỰ LUẬN
Trong một phòng thí nghiệm, người ta nuôi một loại vi khuẩn. Lúc đầu có 300 vi khuẩn. Sau một giờ, số vi khuẩn là 705 con. Giả sử số vi khuẩn tăng lên theo công thức tăng trưởng mũ, số vi khuẩn sau \(x\) giờ là \(f\left( x \right) = C.{e^{kx}}\). Tính số lượng vi khuẩn có được sau 5 giờ. (kết quả làm tròn đến hàng phần mười).
Giải bất phương trình \({\log _2}x > 3\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của cạnh \(AB\). Gọi \(M\) là trung điểm của cạnh \(AD\). Chứng minh \(CM\) vuông góc với mặt phẳng \(\left( {SHD} \right)\).