Bộ 5 đề thi giữa kì 1 Toán 9 Kết nối tri thức cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Xác định hệ số \[a,\,\,b,\,\,c\] của phương trình bậc nhất hai ẩn \[2x-5y = 7\] ta được
\[a = 2,{\rm{ }}b = 5,{\rm{ }}c = 7.\]
\[a = - 5,{\rm{ }}b = 2,{\rm{ }}c = 7.\]
\[a = 5,{\rm{ }}b = 2,{\rm{ }}c = 7.\]
\[a = 2,{\rm{ }}b = - 5,{\rm{ }}c = 7.\]
Giá trị \(x = 0\) và \(x = - 1\) là nghiệm của phương trình nào sau đây?
\(x\left( {x - 1} \right) = 0\).
\(x\left( {x + 1} \right) = 0\).
\(x = 0\).
\(\left( {x - 1} \right)\left( {x + 1} \right) = 0\).
Cho hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\ - 2x + 4y = - 1\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\) và các khẳng định nào sau:
(i) Nhân hai vế của phương trình (1) với 2, rồi cộng từng vế với phương trình (2), ta nhận được phương trình \(0x = 3.\)
(ii) Nhân hai vế của phương trình (1) với 2, rồi cộng từng vế với phương trình (2), ta nhận được phương trình có vô số nghiệm.
(iii) Hệ phương trình đã cho vô nghiệm.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
0.
1.
2.
3.
Tập hợp \(S = \left\{ {\left( {x\,;\,\,\frac{2}{3}x + \frac{5}{3}} \right)|x \in \mathbb{R}} \right\}\) là tập nghiệm của phương trình nào dưới đây?
\[ - 2x + 3y = 5.\]
\[2x + 3y = 5.\]
\[3x--2y = 5.\]
\[2x--3y = 5.\]
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x + 2}} + 1 = \frac{3}{{x - 3}}\) là
\(x \ne 2.\)
\(x \ne 3.\)
\(x \ne - 2;x \ne 3.\)
\(x \ne - 3;x \ne 2.\)
Tổng các nghiệm của phương trình \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\) là
\(5\).
\(1\).
\( - 5\).
\( - 1\).
Nếu \[a < b\] thì . Dấu thích hợp điền vào ô trống là
\[ \ge \].
\[ \le \].
\[ < \].
\[ > \].
Biết rằng \(m > n\) với \(m,\,\,n\) bất kỳ, chọn câu đúng.
\(n + 2 > m + 2\).
\(m + 3 < n + 3\).
\(m - 2 < n - 2\).
\(m - 3 > n - 3\).
Trong hình bên, \(\cos \alpha \) bằng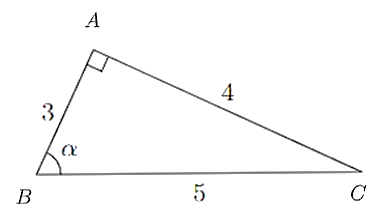
\(\frac{3}{5}.\)
\(\frac{3}{4}.\)
\(\frac{3}{4}.\)
\(\frac{4}{5}.\)
Giá trị \(\cot 35^\circ 23'\) (kết quả làm tròn đến chữ số thập phân thứ ba) là
\(1,408.\)
\(1,409.\)
\(1,407.\)
\(1,440.\)
Cho \(\alpha = 40^\circ \) và \(\beta = 50^\circ .\) Khẳng định nào sau đây là đúng?
\(\sin \alpha = \sin \beta \).
\(\cos \alpha = \cos \beta \).
\(\tan \alpha = \cot \beta \).
\(\tan \alpha = \tan \beta \).
Cho tam giác \(ABC\)vuông tại \(A\)có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?
\(12,45\)cm.
\(15,56\,\,{\rm{cm}}{\rm{.}}\)
\(6,43\,\,{\rm{cm}}{\rm{.}}\)
\(8\)cm.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\) bằng phương pháp cộng đại số theo các bước:
a) Nhân hai vế của phương trình thứ hai với 2, ta được: \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\)
b) Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ, ta được\(0x = 1\).
c) Phương trình \(0x = 1\) vô số nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {6y + 5;\,\,2x - 4} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Cho bất phương trình \(m\left( {5x - 2} \right) < 1\).
a) Bất phương trình đã cho là bất phương trình bậc nhất ẩn \(x\) với \(m \in \mathbb{R}\) tùy ý.
b) Khi \(m = 1,\) bất phương trình đã cho có nghiệm là \(x < \frac{3}{5}\).
c) Khi \(m = - 1,\) bất phương trình đã cho có nghiệm là \(x < \frac{1}{5}\).
d) Khi \(m = - 2,\) bất phương trình đã cho có nghiệm nguyên lớn nhất là \( - 1\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Cho hệ phương trình \(\left\{ \begin{array}{l}x - 5y = 21\\ - 6x + 3y = - 45\end{array} \right.\). Biết cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình. Tính giá trị của \(T = {x_0} + {y_0}.\)
Với giá trị nào của \(x\) thì hai biểu thức \(A = \frac{3}{{3x + 1}} + \frac{2}{{1 - 3x}}\) và \(B = \frac{{x - 5}}{{9{x^2} - 1}}\) có cùng một giá trị?
Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại \(180\,\,{\rm{ml}}\) nặng trung bình \(10\,\,{\rm{kg}}.\) Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là \(5,25\) tấn. Hỏi xe có thể chở được tối đa bao nhiêu thùng sữa như vậy, biết bác lái xe nặng \(65\,\,kg?\)
Cho tam giác \(ABC\) có \(AB = 5{\rm{\;cm}},\,\,BC = 12{\rm{\;cm}}\) và \(CA = 13{\rm{\;cm}}.\) Tính số đo góc \(C\) (làm tròn kết quả đến độ).
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Người ta cho thêm \[1\] kg nước vào dung dịch \[A\] (của axit \(X)\) thì được dung dịch \[B\] có nồng độ axit là \[20\% \]. Sau đó lại cho thêm \[1\] kg axit \(X\) vào dung dịch \[B\] thì được dung dịch \[C\] có nồng độ axit là \[33\frac{1}{3}\% \]. Tính nồng độ axit của dung dịch \[A\].
(1,5 điểm) Lúc 6 giờ sáng, bạn An đi từ nhà (điểm \[A)\] đến trường (điểm \[B)\] phải leo lên và xuống một con dốc đỉnh \(C\) được mô tả như hình vẽ dưới. Cho biết đoạn \[AB\] dài 762 m, \(\widehat {A\,\,} = 4^\circ ,\,\,\widehat {B\,} = 6^\circ .\)
![Lúc 6 giờ sáng, bạn An đi từ nhà (điểm \[A)\] đến trường (điểm \[B)\] phải leo lên và xuống một con dốc đỉnh \(C\) được mô tả như hình vẽ dưới. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/19-1758193340.png)
(0,5 điểm) Một nhóm học sinh tham gia một kỳ thi và có tổng cộng 40 điểm. Nếu biết rằng không có học sinh nào có điểm dưới 10 và tổng số điểm của các học sinh là 300. Chứng minh rằng không có học sinh nào có điểm lớn hơn 30.








