Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\(2{x^2} + 2 = 0.\)
\(3y - 1 = 5\left( {y - 2} \right).\)
\(2x + \frac{y}{2} = 1.\)
\(3\sqrt x + {y^2} = 0.\)
Hệ phương trình nào dưới đây là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}3{x^2} + y = 7\\{x^2} - y = - 1\end{array} \right.\).
\(\left\{ \begin{array}{l}3x + 2y = 8\\ - 2x + y = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}2{x^2} + y = 5\\x - 2{y^2} = - 1\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y = 0\\x + \frac{1}{{{y^2}}} = 3\end{array} \right.\).
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x - 1}} + \frac{{x - 2}}{{{x^2}}} = 2\) là
\(x \ne 1,{\rm{ }}x \ne 0.\)
\(x \ne 1,\,\,x > 0\).
\(x \ne - 1,{\rm{ }}x \ne 0.\)
\(x \ne - 1,{\rm{ }}x > 0.\)
Phát biểu “\(x\) không nhỏ hơn \( - \frac{5}{2}\)” được viết là
\(x > - \frac{5}{2}.\)
\(x \ge - \frac{5}{2}.\)
\(x < - \frac{5}{2}.\)
\(x \le - \frac{5}{2}.\)
Rút gọn \[\sqrt[3]{{{{\left( {x - 1} \right)}^3}}}\] ta được
\(\left| {x - 1} \right|.\)
\(1 - x.\)
\(x - 1.\)
Cả A, B, C đều sai.
Điều kiện xác định của căn thức \(\sqrt {\frac{2}{{x - 1}}} \) là
\(x \ge 1.\)
\(x > 1.\)
\(x < 1.\)
\(x \le 1.\)
Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}} \) bằng
\(3 - 2x.\)
\(2x - 3.\)
\(2x - 3\) và \( - 2x + 3\).
\(\left| {2x - 3} \right|.\)
Giá trị của biểu thức \({\sin ^2}45^\circ + {\cos ^2}45^\circ \) bằng bao nhiêu?
\(0.\)
\(1.\)
\(2.\)
\(4.\)
Với mọi góc nhọn \(\alpha \), ta có
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\tan \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = 1 - \tan \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = \sin \alpha .\)
Cho đường tròn \(\left( {O;{\rm{ 4 cm}}} \right)\) và \(\left( {O';{\rm{ 3 cm}}} \right)\) có \(OO' = 5{\rm{ cm}}{\rm{.}}\) Vị trí tương đối của hai đường tròn đã cho là
tiếp xúc trong.
cắt nhau.
tiếp xúc ngoài.
đựng nhau.
Góc ở tâm chắn cung \(160^\circ \) có số đo bằng bao nhiêu?
\(200^\circ .\)
\(160^\circ \).
\(80^\circ \).
\(20^\circ .\)
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Khẳng định nào sau đây là sai?
Khoảng cách từ điểm đó đến hai tiếp tuyến bằng nhau.
Tia kẻ từ điểm đó qua tâm là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Tia kẻ từ tâm qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Tia kẻ từ điểm đó qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Lan có một dung dịch nước muối sinh lí có nồng độ \(1,5\% \) và một dung dịch nước cất không chứa muối (nồng độ \(0\% \)). Lan cần pha trộn dung dịch để thu được 1 lít (1000 ml) dung dịch nước muối dinh lí súc miệng có nồng độ 0,9%. Gọi (ml) là thể tích dung dịch nước muối và \(y\) (ml) là thể tích nước cất \(0\% \) (\(x,{\rm{ }}y > 0\)).
a) Phương trình biểu diễn tổng thể tích dung dịch là \(x + y = 1\,\,000\).
b) Phương trình biểu diễn lượng muối trong dung dịch ban đầu là .
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}x + y = 1\,\,000\\0,015x + y = 900\end{array} \right.\).
d) Lan cần pha \(600{\rm{ ml}}\) dung dịch nước muối \(1,5\% \) và \(400{\rm{ ml}}\) dung dịch nước cốt \(0\% \) để được dung dịch mong muốn.\(1,5\% .x\)
Một người quan sát một tòa nhà và đứng cách tòa nhà khoảng \[25{\rm{\;m}}\]. Góc nâng từ mắt người quan sát đến nóc tòa nhà là \[36^\circ \]. Nếu anh ta đi thêm \[5{\rm{\;m}}\] nữa, đến vị trí \[E\] nằm giữa \[C\] và \[H\], thì có góc nâng mới từ \[F\] đến nóc tòa nhà. Chiều cao \[CD\] tính từ chân đến mắt người quan sát là \[1,6{\rm{\;m}}{\rm{.}}\] (Các kết quả làm tròn đến hàng đơn vị)
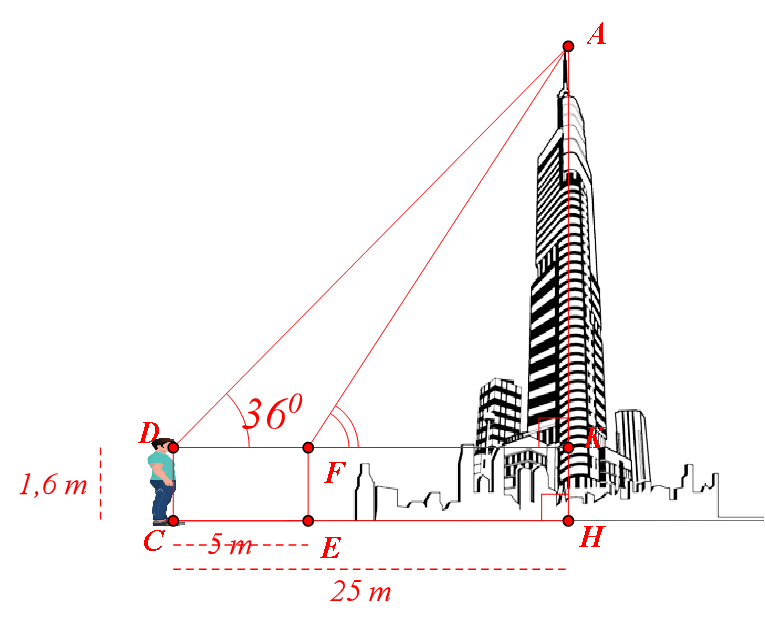
a) \[AK = KD \cdot \tan 36^\circ .\]
b) \[FK = 25{\rm{\;m}}{\rm{.}}\]
c) Độ dài tòa nhà lớn hơn 20 m.
d) Góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}} = \frac{{12}}{{1 - 9{x^2}}}.\)
Tìm giá trị nguyên nhỏ nhất của \(x\) thỏa mãn của bất phương trình \(\frac{{3x + 5}}{2} - 1 < \frac{{2x + 1}}{3} + x\).
Tính giá trị của biểu thức \[A = \frac{{\sqrt x - 2}}{{\sqrt x + 7}}\] tại \[x = 25.\] (Kết quả ghi dưới dạng số thập phân)
Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \[T = \left( {\frac{{a\sqrt a - 1}}{{a - \sqrt a }} - \frac{{a\sqrt a + 1}}{{a + \sqrt a }}} \right):\frac{{a + 1}}{{a - 1}}\] với \[a > 0,{\rm{ }}a \ne 1\].
a) Chứng minh rằng \[T = \frac{{2\left( {a - 1} \right)}}{{a + 1}}\].
b) Tìm các giá trị nguyên của \[a\] để \[T\] nhận giá trị nguyên.
(1,5 điểm)Cho nửa đường tròn tâm \[O\] đường kính \[AB = 2R\]. Từ \[A\] kẻ tiếp tuyến\[Ax\], \[P \in Ax\]sao cho \[AP > R.\] Từ \[P\] kẻ tiếp tuyến \[PM\] với \[\left( O \right)\] tại \[M.\] Gọi \[OP\] cắt \[MA\] tại \[Q\]. Đường vuông góc với \[AB\] tại \[O\] cắt \[BM\] tại \[N.\]
a) Chứng minh bốn điểm \[A,\,P,\,M,\,O\] cùng thuộc một đường tròn.
b) Chứng minh tứ giác \[OBNP\] là hình bình hành và gọi \[PM\] cắt \[ON\] tại \[I\]. Chứng minh \[\Delta POI\] cân.
c) Gọi \[PN\] cắt \[OM\] tại \[J,\,AN\] cắt \[OP\] tại \[K.\] Chứng minh ba điểm \[I,\,J,\,K\] thẳng hàng.
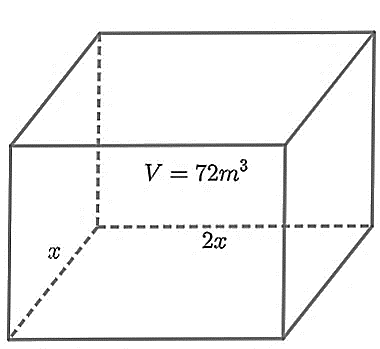
(0,5 điểm) Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng \(72{\rm{ }}{{\rm{m}}^3}\). Đáy bể có dạng hình chữ nhật với chiều rộng là \(x{\rm{ }}\left( {\rm{m}} \right)\), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì \(x\) phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?