Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\(\frac{x}{2} + \frac{y}{3} = 4.\)
\(3x - 0y - 2 = 0.\)
\(3y - 2z = \frac{1}{2}.\)
\(\frac{2}{x} + \frac{y}{3} - 2 = 0.\)
Trong các hệ phương trình dưới đây, hệ phương trình nào không phải là hệ hai phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x - 3y = 5\\2y - x = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y = 4\\2x - \sqrt 5 y = 3\end{array} \right.\).
\(\left\{ \begin{array}{l} - x + 3y = - 4\\3x - 2y = 1\end{array} \right.\).
\(\left\{ \begin{array}{l}2x + y = 1\\x - 3{y^2} = 4\end{array} \right.\).
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} - 1 = \frac{{30}}{{\left( {x + 3} \right)\left( {x - 4} \right)}}\) là
\(x \ne - 3;{\rm{ }}x \ne 4.\)
\(x \ne 3;{\rm{ }}x \ne - 4.\)
\(x \ne - 3;{\rm{ }}x \ne 4;{\rm{ }}x \ne - 2.\)
\(x \ne - 3;{\rm{ }}x \ne - 4.\)
Bất đẳng thức diễn tả khẳng định “\(n\) nhỏ hơn \(\frac{3}{5}\)” là
\(n \le \frac{3}{5}.\)
\(n < \frac{3}{5}.\)
\(n > \frac{3}{5}.\)
\(n \ge \frac{3}{5}.\)
Điều kiện xác định của biểu thức \(A = \sqrt {1 - 2x} \) là
\(x \le \frac{1}{2}.\)
\(x < \frac{1}{2}.\)
\(x > \frac{1}{2}.\)
\(x \ge \frac{1}{2}.\)
Cho hai biểu thức \(A\) và \(B\). Khẳng định nào sau đây là sai?
\(\sqrt {AB} = \sqrt A \cdot \sqrt B \) với \(A \ge 0,\,\,B \ge 0\).
\(\sqrt {AB} = \sqrt { - A} \cdot \sqrt { - B} \) với \(A < 0,\,\,B < 0\).
\(\sqrt {\frac{A}{B}} = \frac{{\sqrt A }}{{\sqrt B }}\) với \(A \ge 0,\,\,B \ge 0\).
\(\sqrt {\frac{A}{B}} = \frac{{\sqrt { - A} }}{{\sqrt { - B} }}\) với \(A < 0,\,\,B < 0\).
Trục căn thức ở mẫu của \(\frac{2}{{\sqrt 3 - 1}}\) được kết quả là
\(2\left( {\sqrt 3 + 1} \right).\)
\(2\left( {\sqrt 3 - 1} \right).\)
\(\sqrt 3 + 1.\)
\(\sqrt 3 - 1.\)
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó:
\(AB = AC.\cos B.\)
\(AB = AC.\cos C.\)
\(AB = BC.\cos B.\)
\(AB = BC.\cos C.\)
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \(\alpha + \beta = 90^\circ \). Khẳng định nào sau đây là đúng?
\(\tan \alpha = \sin \beta .\)
\(\tan \alpha = \cot \beta .\)
\(\tan \alpha = \cos \beta .\)
\(\tan \alpha = \tan \beta .\)
Điểm \(M\) nằm trên đường tròn \(\left( {O;\,\,R} \right)\) nếu
\(OM = R.\)
\(OM > R.\)
\(OM < R.\)
\(OM = 2R.\)
Cho hai đường tròn \(\left( {O;\,\,2{\rm{ cm}}} \right)\) và \(\left( {O';\,\,5{\rm{ cm}}} \right)\) tiếp xúc ngoài thì độ dài của \(OO'\) bằng:
\(2{\rm{ cm}}.\)
\({\rm{7 cm}}.\)
\({\rm{3 cm}}.\)
\({\rm{1 cm}}.\)
Cho hai đường tròn đồng tâm \(O\) có bán kính lần lượt là \(R\) và \(r{\rm{ }}\left( {R > r} \right).\) Diện tích phần nằm giữa hai đường tròn này – hình vành khăn được tính
\(S = \pi \left( {{r^2} - {R^2}} \right).\)
\(S = \pi \left( {{r^2} + {R^2}} \right).\)
\(S = \pi \left( {{R^2} - {r^2}} \right).\)
Kết quả khác.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Hai tổ cùng làm một công việc trong \(15\) giờ thì xong. Nếu tổ I làm trong \(3\) giờ, tổ II làm trong \(5\) giờ thì được \(25\% \) công việc. Gọi \(x,\,\,y\) (giờ) lần lượt là số giờ tổ I, tổ II làm riêng để hoàn thành toàn bộ công việc \(\left( {x,\,\,y > 0} \right).\)
a) Trong 1 giờ, tổ I làm được \(\frac{1}{x}\) (công việc); tổ II làm được \(\frac{1}{y}\) (công việc).
b) Trong 3 giờ, tổ I làm được \(\frac{3}{x}\) (công việc); trong 5 giờ tổ II làm được \(\frac{5}{y}\) (công việc).
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = 15\\\frac{3}{x} + \frac{5}{y} = \frac{1}{4}\end{array} \right.\).
d) Nếu làm riêng thì tổ I hoàn thành công việc trong 40 giờ, tổ II hoàn thành trong 24 giờ.
Một người có tầm mắt cao \[1,65{\rm{ m}}\] đứng trên tầng thượng của tòa Lotte Center thì nhìn thấy một chiếc xe thu gom phế thải đang dừng ở \[B\] với góc nghiêng \[80^\circ \] (như hình vẽ). Biết xe đó cách tòa nhà \(48{\rm{ m}}\). Lúc này, một người ở độ cao \[200{\rm{ m}}\] của tòa nhà cũng nhìn thấy xe thu gom phế thải khác đang dừng ở \[E\] với góc nghiêng \(65^\circ \). (Tất cả các kết quả làm tròn đến hàng phần trăm)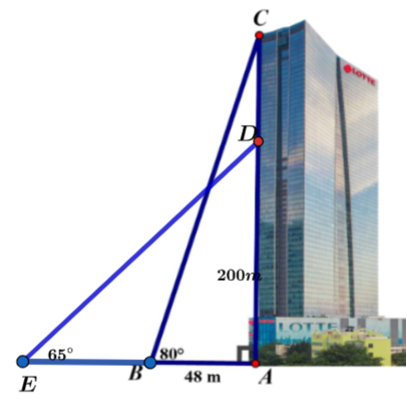
a)\(AC = AB.\cot \widehat {CBA}\).
b) Tòa nhà có độ cao lớn hơn \(272{\rm{ m}}{\rm{.}}\)
c) Khoảng cách từ xe thu gom phế thải ở \(E\) đến chân tòa nhà khoảng \(93,26{\rm{ m}}{\rm{.}}\)
d) Hai xe thu gom phế thải cách nhau một khoảng lớn hơn \(45{\rm{ m}}{\rm{.}}\)
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình \(\frac{{2x - 5}}{{x - 3}} - \frac{1}{x} = \frac{{6x + 3}}{{{x^2} - 3x}}\)?
Hỏi giá trị nguyên lớn nhất của \(x\) thỏa mãn bất phương trình \[\frac{{x + 1}}{3} - \frac{{x - 2}}{2} \ge 4\] là bao nhiêu?
Tính giá trị của biểu thức \(B = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}\) khi \(x = \frac{1}{{16}}.\) (Kết quả ghi dưới dạng số thập phân)
Cung tròn \(50^\circ \) của một đường tròn có độ dài là \(\pi {\rm{\;cm}}.\) Tính bán kính của đường tròn đó.
(Kết quả ghi dưới dạng số thập phân)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cho biểu thức \(P = \left( {\frac{{x - 2}}{{x + 2\sqrt x }} + \frac{1}{{\sqrt x + 2}}} \right) \cdot \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\) với \(x > 0\) và
a) Chứng minh rằng \(P = \frac{{\sqrt x + 1}}{{\sqrt x }}.\)
b) Tìm các giá trị của \(x\) để \(2P = 2\sqrt x + 5\).
(1,5 điểm) Cho nửa đường tròn \[\left( O \right)\] đường kính \[AB\]. Lấy \[C\] nằm trên đường tròn \[\left( O \right)\]. Gọi \[K\] là trung điểm của dây cung \[BC\]. Qua \[B\] dựng tiếp tuyến với \[\left( O \right)\], cắt \[OK\] tại \[D\].
a) Chứng minh rằng \[OD \bot BC\] và \[\Delta ABC\] vuông.
b) Chứng minh \[DC\] là tiếp tuyến của đường tròn \[\left( O \right)\].
c) Vẽ \[CH \bot AB\] tại \[H\]. Gọi \[I\] là trung điểm của \[CH\]. Tiếp tuyến tại \[A\] của đường tròn \[\left( O \right)\] cắt \[BI\] tại \[E\]. Chứng minh \[E,C,D\] thẳng hàng.
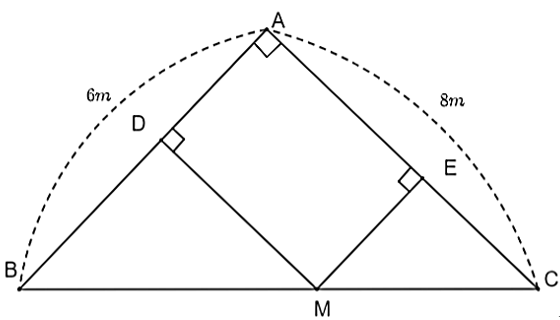
(0,5 điểm) Một người đào ao cá trên thửa ruộng dạng hình tam giác vuông \[ABC\] tại \[A\] có độ dài các cạnh góc vuông \[AB = 6{\rm{ m,}}\] \[AC = 8{\rm{ m}}{\rm{.}}\] Một chiếc máy xúc ở vị trí điểm \[M\] di chuyển trên bờ \[BC.\] Gọi \[MD\] và \[ME\] là khoảng cách từ \[M\] đến bờ \[AB,AC.\] Người đó đào được ao là tứ giác \[ADME\]. Tính diện tích lớn nhất của ao cá mà người đó có thể đào.