Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\(5x - y = 3.\)
\(\sqrt 3 x + 0y = 3.\)
\(0x + 2y = \sqrt 7 .\)
\(0x + 0y = 4.\)
Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y = 1\\2x - y = - 1\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2{y^2} = 4\\x + y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2y = 4\\3{x^2} - 2y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} + 2{y^2} = 4\\3x - y = 0\end{array} \right..\)
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x + 2}} + 1 = \frac{3}{{x - 3}}\) là
\(x \ne 2.\)
\(x \ne 3.\)
\(x \ne - 2;{\rm{ }}x \ne 3.\)
\(x \ne - 3;{\rm{ }}x \ne 2.\)
Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn?
\(x + 2y > 0.\)
\(\frac{1}{x} - 3 > 0.\)
\({x^2} + 1 > 0.\)
\(\frac{x}{2} + 1 > 0.\)
Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?
\({\left( { - \sqrt 5 } \right)^2}.\)
\(\sqrt {{5^2}} .\)
\(\sqrt {{{\left( { - 5} \right)}^2}} .\)
\( - {\left( {\sqrt 5 } \right)^2}.\)
Với mọi số \(a\), ta luôn có:
\(\sqrt {{a^2}} = a.\)
\(\sqrt {{a^2}} = \left| a \right|.\)
\(\sqrt a = \left| a \right|.\)
\(\sqrt {{a^2}} = - a.\)
Điều kiện xác định của căn thức \(\sqrt {2x + 3} \) là
\(x \ge \frac{{ - 3}}{2}.\)
\(x \le \frac{{ - 3}}{2}.\)
\(x \ge \frac{{ - 2}}{3}.\)
\(x \le \frac{{ - 2}}{3}.\)
Cho tam giác vuông có \(\alpha \) là góc nhọn. Khẳng định nào sau đây là sai?
Tỉ số giữa cạnh huyền và cạnh kề được gọi là cosin của góc \(\alpha \), kí hiệu \(\sin \alpha .\)
Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \alpha .\)
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \), kí hiệu \(\tan \alpha .\)
Tỉ số giữa cạnh kề và cạnh đối được gọi là tang của góc \(\alpha \), kí hiệu \(\cot \alpha .\)
Nếu \(\alpha \) là góc nhọn thì \[\sin \left( {90^\circ - \alpha } \right)\] bằng
\(\sin \alpha .\)
\(\tan \alpha .\)
\(\cos \alpha .\)
\(\cot \alpha .\)
Điền từ thích hợp vào chỗ trống: “Đường tròn có …. trục đối xứng”.
1.
0.
Vô số.
2.
Cho đường tròn \(\left( {O;\,\,6{\rm{ cm}}} \right)\) và đường thẳng \(a\) với khoảng cách từ \(O\) đến \(a\) là \(4\,\,{\rm{cm}}.\) Kết luận nào sau đây đúng về vị trí giữa đường tròn \(\left( O \right)\) và đường thẳng \(a\)?
\(\left( O \right)\) và \(a\) cắt nhau tại hai điểm.
\(\left( O \right)\) và \(a\) tiếp xúc.
\(\left( O \right)\) và \(a\) không có điểm chung.
\(\left( O \right)\) và \(a\) có duy nhất một điểm chung.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Lớp 9A và lớp 9B có tổng cộng \(86\) học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được \(5{\rm{ kg}}\), các bạn còn lại mỗi bạn góp \({\rm{2 kg}}{\rm{.}}\) Biết rằng lớp 9B góp nhiều hơn lớp 9A là \({\rm{8 kg}}\) giấy báo cũ. Gọi \(x\) là số học sinh của lớp 9A, \(y\) là số học sinh của lớp 9B \(\left( {x,{\rm{ }}y \in {\mathbb{N}^ * }} \right)\).
a)\(x + y = 86.\)
b) Phương trình biểu diễn mối liên hệ khối lượng giấy báo cũ giữa hai lớp là \(2x - 2y = 8.\)
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}x + y = 86\\y - x = 4\end{array} \right.\).
d) Lớp 9A có \(41\) học sinh, lớp 9B có \(45\) học sinh.
Đường thẳng \(d\) cách tâm \(O\) của đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) một khoảng \({\rm{3 cm}}.\) Khi đó vị trí tương đối của \(d\) và đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) là
Cắt nhau.
Không giao nhau.
Tiếp xúc nhau.
Không kết luận được.
Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Hai người đứng cách nhau \(250{\rm{ m}}\) như hình minh họa dưới đây. (Kết quả làm tròn đến hàng phần trăm)
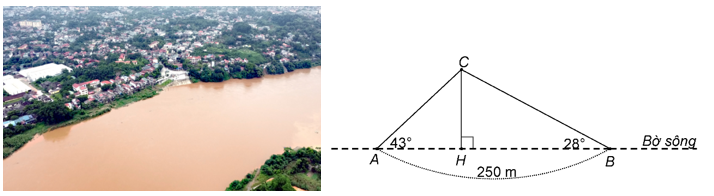
a)\(CH = AH \cdot \tan 43^\circ .\)
b)\(BH = \frac{{CH}}{{\tan 28^\circ }}.\)
c)\(AB = \left( {\tan 43^\circ + \tan 28^\circ } \right)CH\).
d) Cồn cách bờ sông hai người đứng một khoảng lớn hơn \(85{\rm{ m}}{\rm{.}}\)
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{x + 3}}{{x - 2}} - \frac{{x + 1}}{{x + 2}} = \frac{{{x^2} - 4x + 24}}{{{x^2} - 4}}\).
Tìm nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình: \(3x - \left( {6 + 2x} \right) \le 3 \cdot \left( {x + 4} \right)\).
Tính giá trị của biểu thức \(A = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{2\left( {1 - \sqrt x } \right)}}\) với \(x = \frac{1}{{25}}.\)(Kết quả ghi dưới dạng số thập phân)
Một chiếc đèn thả hình vành khuyên, rỗng ở giữa. Biết đường kính của đường tròn lớn là \(90\,{\rm{cm}}\), đường kính của đường tròn nhỏ là \(60\,{\rm{cm}}\). Hỏi diện tích của chiếc đèn bằng bao nhiêu mét vuông? (Kết quả làm tròn đến hàng phần trăm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \(A = \frac{3}{{\sqrt a + 3}}:\left( {\frac{{\sqrt a - 2}}{{\sqrt a + 3}} + \frac{{\sqrt a - 3}}{{2 - \sqrt a }} - \frac{{9 - a}}{{a + \sqrt a - 6}}} \right)\) với \(a \ge 0,{\rm{ }}a \ne 4\) và \(a \ne 9.\)
a) Chứng minh rằng \(A = \frac{3}{{\sqrt x - 2}}\).
b) Tìm \(a\) để \(A + \left| A \right| = 0.\)
(1,5 điểm)Cho nửa đường tròn tâm \(O\) đường kính \(AB = 2R,\)\(D\) là một điểm tùy ý trên nửa đường tròn (\(D\) khác \(A\) và \(D\) khác \(B\)). Các tiếp tuyến với nửa đường tròn \(\left( O \right)\) tại \(A\) và \(D\) cắt nhau tại \(C,{\rm{ }}BC\) cắt nửa đường tròn \(\left( O \right)\) tại điểm \(E\) (\(E\) nằm giữa \(C\) và \(B\)). Kẻ \(DF \bot AB\) tại \(F\).
a) Chứng minh bốn điểm \(O,\,\,A,\,\,C,\,\,D\) cùng thuộc một đường tròn.
b) Chứng minh đường thẳng \(BC\) đi qua trung điểm của \(DF\).
c) Giả sử \(OC = 2R,\) tính diện tích phần tam giác \(ACD\) nằm ngoài nửa đường tròn \(\left( O \right)\) theo \(R.\)
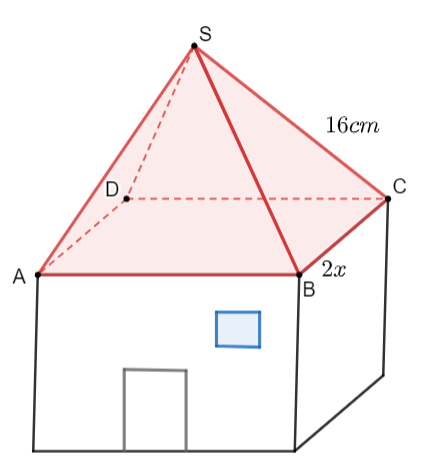
(0,5 điểm)Bạn Nam làm một căn nhà đồ chơi bằng gỗ có phần mái là một chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn Nam dùng các thanh gỗ có chiều dài \(16{\rm{ cm}}\). Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là \(2x{\rm{ }}\left( {{\rm{cm}}} \right)\). Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?