Bộ 5 đề thi giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 3
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như hình vẽ bên dưới.
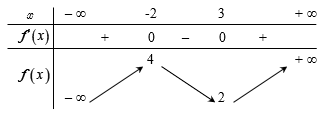
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
\[\left( {2;4} \right)\].
\[\left( { - \infty ;4} \right)\].
\[\left( {3; + \infty } \right)\].
\[\left( {2; + \infty } \right)\].
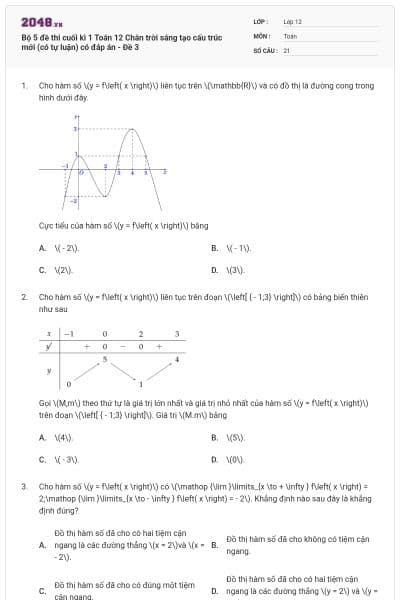
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên dưới.
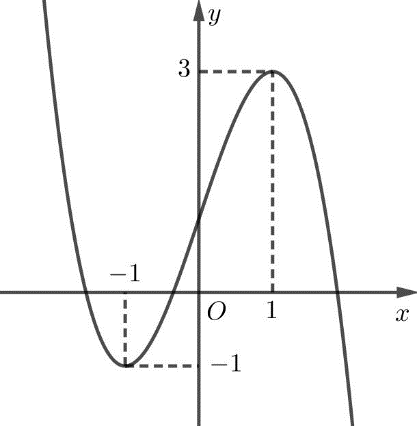
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là
\(\left( {3;1} \right)\).
\(\left( { - 1; - 1} \right)\).
\(\left( {1;3} \right)\).
\(\left( {1;\, - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là sai?
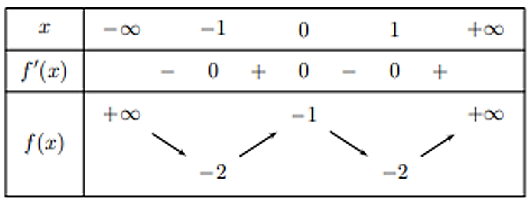
Hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng \( - 2\).
Hàm số \(y = f\left( x \right)\) không có giá trị lớn nhất.
Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất bằng \[ - 1\]
Hàm số \(y = f\left( x \right)\) đạt giá trị nhỏ nhất tại \( \pm 1\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) là đường thẳng có phương trình
\(x = - 1.\)
\(y = - 1.\)
\(x = 2.\)
\(y = 2.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên được cho dưới đây.
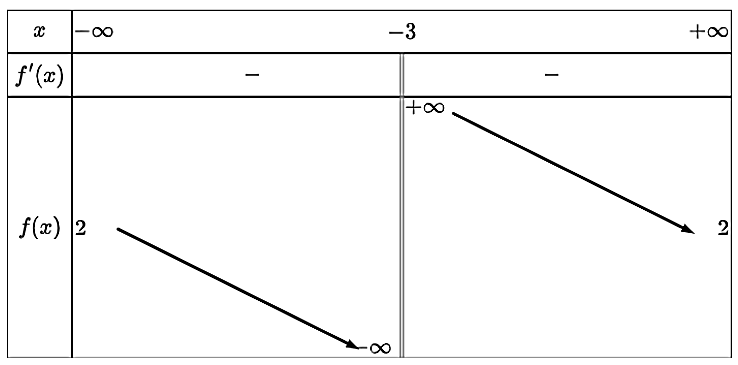
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\) là
2
3
0
1
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình sau:
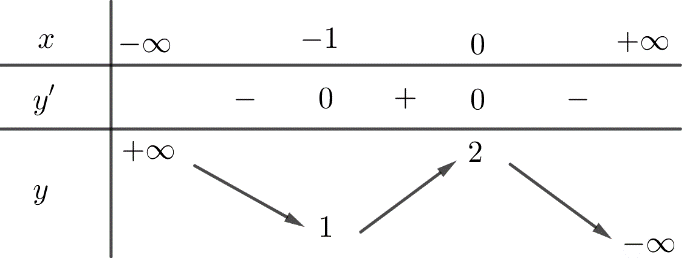
Số giao điểm của đồ thị hàm số đã cho với trục hoành là
0
2
3
1
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
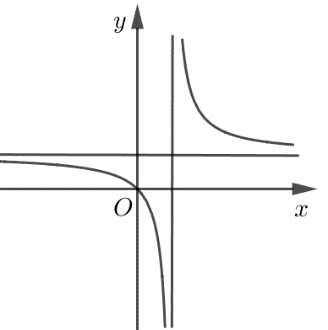
\(y = \frac{{x - 2}}{{x + 1}}\).
\(y = \frac{x}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = \frac{x}{{x + 1}}\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Chọn khẳng định đúng.
\[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} - \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} - \overrightarrow {DC} - \overrightarrow {DS} \].
\[\overrightarrow {SB} = \overrightarrow {DA} - \overrightarrow {DC} + \overrightarrow {DS} \].
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
\(\overrightarrow a \cdot \overrightarrow b = 0\).
\(\overrightarrow a \cdot \overrightarrow b = - 1\).
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\)
Cho hàm số \[y = f\left( x \right) = {x^3} + 3{x^2} - 1\]. Giá trị cực đại của hàm số đã cho là
-1
0
-2
3
Hàm số nào có bảng biến thiên như hình dưới đây?
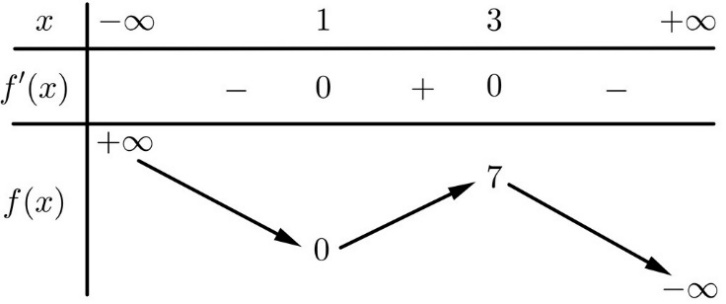
\[y = - \frac{7}{4}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x + 7\].
\[y = \frac{7}{4}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x + 7\].
\[y = - \frac{5}{3}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x\].
\[y = \frac{5}{3}{x^3} + \frac{{21}}{2}{x^2} - \frac{{63}}{4}x\].
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(O,O'\) lần lượt là tâm của hình vuông \(ABCD\) và \(A'B'C'D'\). Độ dài vec tơ \(\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \) bằng
4a
6a
2a
a
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Hỏi hàm số có đồ thị \(\left( C \right)\).
a) Đồ thị \(\left( C \right)\)có tiệm cận đứng là đường thẳng \(x = - 1\).
b)Đường thẳng\(y = x + 1\)là tiệm cận xiên của đồ thị \(\left( C \right)\).
c)Hàm số nghịch biến trên khoảng \(\left( { - 4; - 1} \right)\) và \(\left( { - 1;2} \right)\).
d) Đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị hàm số là \(y = 2x + 3\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) và \(AB = a\), \[AD = b\], \(AA' = c\). Gọi \(M\) là trung điểm của \(B'C'\) và\(G\) là trọng tâm tam giác \(DC'D'\).
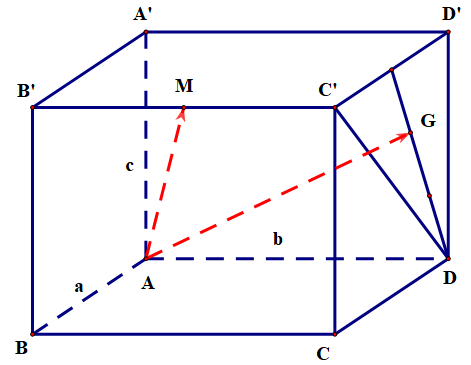
a) Có 3 vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp chữ nhật bằng \(\overrightarrow {AB} \).
b) \(\overrightarrow {AM} = \overrightarrow {AA'} + \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \).
c) \(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AA'} + \overrightarrow {AD} \) và \(AG = \sqrt {\frac{1}{9}{a^2} + \frac{4}{9}{c^2} + {b^2}} \).
d) \(\overrightarrow {AM} \cdot \overrightarrow {AG} = \frac{1}{6}{a^2} + {b^2} + \frac{2}{3}{c^2}\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Số lượng sản phẩm bán được của một công ty trong \(x\) (tháng) được tính theo công thức \(S\left( x \right) = 500\left( {3 - \frac{7}{{3 + x}}} \right)\), trong đó \(x \ge 1\). Số lượng sản phẩm được bán của công ty đó trong \(x\) (tháng) khi \(x\) đủ lớn gần bằng bao nhiêu?
Cho hàm số bậc ba \[y = {x^3} + a{x^2} + bx + c\] có đồ thị như hình vẽ dưới đây.
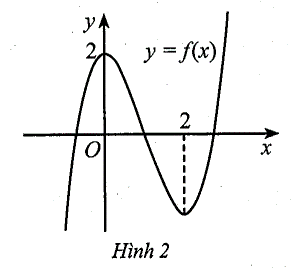
Tính giá trị của \[S = a + 2b + 3c\].
Gọi \(M,\,m\)lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = x + \sqrt {2 - {x^2}} \).
Tính \(M - \sqrt 2 \cdot m\).
Cho hai vectơ \[\overrightarrow a \] và \[\overrightarrow b \] thỏa mãn \[\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 2\sqrt 3 ,\overrightarrow a \cdot \overrightarrow b = - 3\]. Tính \[\left| {2\overrightarrow a + \overrightarrow b } \right|\].
PHẦN II. TỰ LUẬN
Cho hai vị trí \[A,B\]cách nhau \[615\,{\rm{m}}\], cùng nằm về một phía bờ sông. Khoảng cách từ \[A\]và \[B\] đến bờ sông lần lượt là \[118\,{\rm{m}}\] và \[487\,{\rm{m}}\]. Một người đi từ \[A\]đến bờ sông để lấy nước mang về \[B\]. Xác định độ dài đoạn đường ngắn nhất mà người đó có thể đi.
Một thùng rác thông minh cảm ứng tự động đóng mở dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2000m3 Thùng rác được làm bằng nhựa ABS có độ bền cao, chịu nhiệt, cách điện, chống nước. Để lượng vật liệu dùng để sản xuất thùng rác là nhỏ nhất thì chiều cao của chiếc hộp bằng bao nhiêu?

Người ta vận chuyển một thùng hàng có dạng hình hộp chữ nhật bằng cách móc 4 dây cáp vào 4 góc trên của thùng hàng và đầu còn lại móc vào cần cẩu như hình vẽ. Biết rằng các đoạn dây cáp có độ dài bằng nhau và góc tạo bởi hai đoạn dây cáp đối diện nhau là 60°. Chiếc cần cẩu kéo thùng hàng lên theo phương thẳng đứng. Biết rằng \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} ,\,\overrightarrow {{F_3}} ,\,\overrightarrow {{F_4}} \) chịu được tối đa lực căng là 5 000 N. Hỏi cần cẩu nâng được thùng hàng có khối lượng (đơn vị: kg) tối đa là bao nhiêu? Lấy g = 10 m/s2.