Bộ 5 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
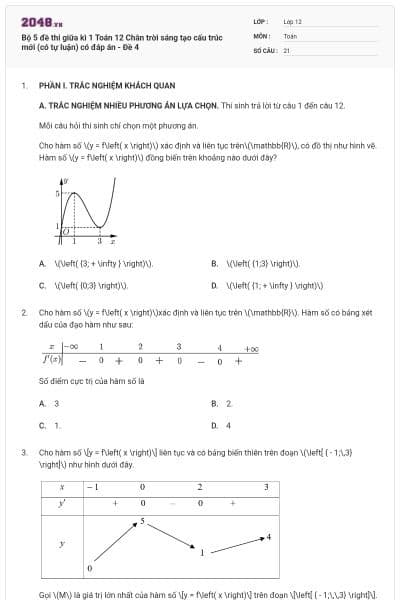
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
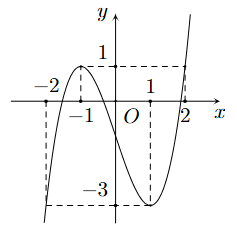
\(\left( {0;2} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - \infty ;1} \right)\).
\(\left( { - 2;1} \right)\).
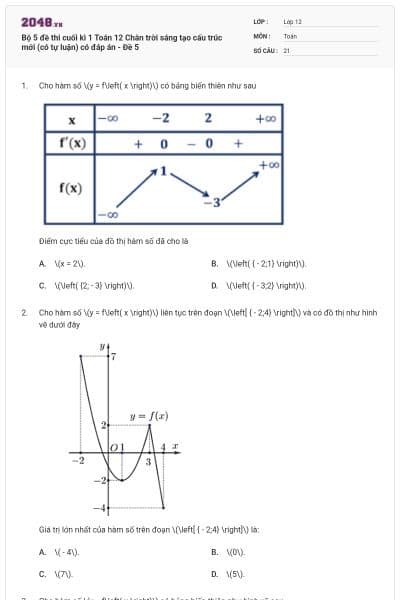
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
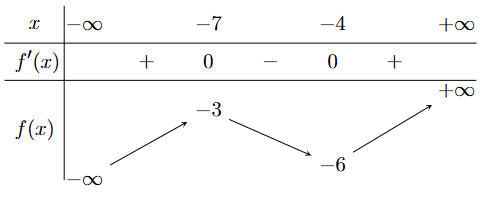
Điểm cực đại của hàm số đã cho là
\(x = - 7\).
\(x = - 4\).
\(x = - 3\).
\(x = - 6\).
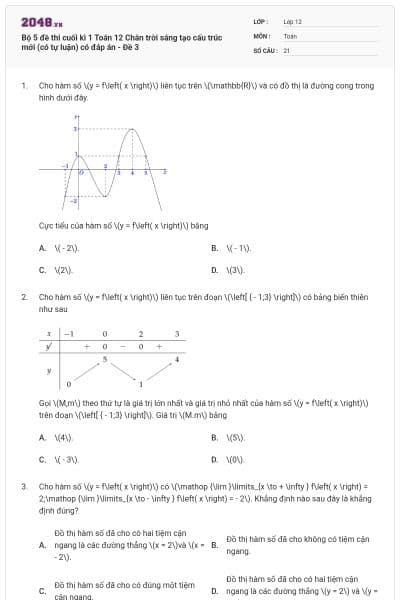
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ {1;3} \right]\). Giá trị của \(M + m\) bằng
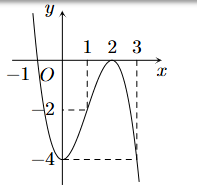
\(4\).
\( - 6\).
\( - 2\).
\( - 4\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong \(\left( C \right)\) và các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\). Hỏi mệnh đề nào sau đây đúng?
Đường thẳng \(y = 2\) là tiệm cận ngang của \(\left( C \right)\).
Đường thẳng \(y = 1\) là tiệm cận ngang của \(\left( C \right)\).
Đường thẳng \(x = 2\) là tiệm cận ngang của \(\left( C \right)\).
Đường thẳng \(x = 2\) là tiệm cận đứng của \(\left( C \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
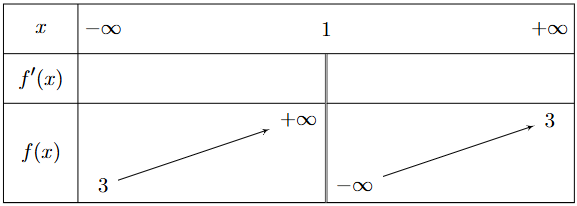
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
\(x = - 1\).
\(x = - 3\).
\(x = 3\).
\(x = 1\).
Đường cong ở hình bên là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào sau đây đúng?
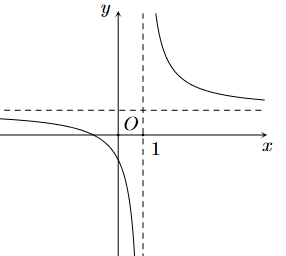
\(y' < 0,\forall x \ne 1\).
\(y' < 0,\forall x \in \mathbb{R}\).
\(y' > 0,\forall x \ne 1\).
\(y' > 0,\forall x \in \mathbb{R}\).
Trong không gian, cho các điểm \(I,N,E\). Tìm khẳng định đúng.
\(\overrightarrow {IN} - \overrightarrow {IE} = \overrightarrow {NE} \).
\(\overrightarrow {IN} + \overrightarrow {IE} = \overrightarrow {NE} \).
\(\overrightarrow {IN} + \overrightarrow {NE} = \overrightarrow {IE} \).
\(\overrightarrow {IE} - \overrightarrow {NE} = \overrightarrow {NI} \).
Cho hình hộp \(ABCD.A'B'C'D'\). Vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ \(\overrightarrow {B'D'} \) là vectơ nào sau đây.
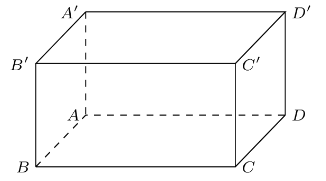
\(\overrightarrow {DB} \).
\(\overrightarrow {D'B'} \).
\(\overrightarrow {BA'} \).
\(\overrightarrow {BD} \).
Trong không gian \(\left( {Oxyz} \right)\), cho \(\overrightarrow {OA} = 3\overrightarrow k - \overrightarrow i \). Tọa độ của điểm \(A\) là
\(A\left( {3; - 1;0} \right)\).
\(A\left( { - 1;3;0} \right)\).
\(A\left( {3;0; - 1} \right)\).
\(A\left( { - 1;0;3} \right)\).
Cho \(\overrightarrow u = \left( { - 2;3;2} \right),\overrightarrow v = \left( {2;1; - 1} \right)\). Tọa độ vectơ \(\overrightarrow u - \overrightarrow v \) bằng
\(\left( {1;2;3} \right)\).
\(\left( {0;4;1} \right)\).
\(\left( { - 4;2;3} \right)\).
\(\left( {4; - 2; - 3} \right)\).
Cho mẫu số liệu ghép nhóm về khoảng tuổi và số người như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
\(16\).
\(3\).
\(61\).
\(60\).
Chọn khẳng định đúng.
Phương sai bằng bình phương số trung bình.
Phương sai bằng bình phương độ lệch chuẩn.
Phương sai bằng căn bậc hai của số trung bình.
Phương sai bằng căn bậc hai của độ lệch chuẩn.
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ
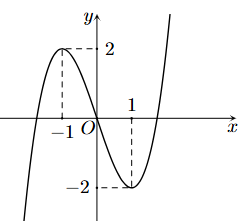
(a) Hàm số đồng biến trên khoảng \(\left( { - 1;1} \right)\).
(b) Giá trị cực đại của hàm số là 2.
(c) Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {\frac{1}{2};2} \right]\) là \( - 1\).
(d) Giá trị của hàm số tại \(x = 5\) là \(f\left( 5 \right) = 100\).
Trong không gian \(Oxyz\), cho \(\Delta ABC\) có \(A\left( {1;0;0} \right),B\left( {0;0;1} \right),C\left( {2;1;1} \right)\).
(a) \(\overrightarrow {AB} = \left( { - 1;0;1} \right)\).
(b) \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \) cùng phương.
(c) \(AB \bot AC\).
(d) Diện tích tam giác \(ABC\) là \(\sqrt 6 \).
Biết đồ thị hàm số \(y = \frac{{{x^2} + 3x + 2}}{{x - 3}}\) có đường tiệm cận xiên \(y = g\left( x \right) = ax + b\). Tính \(g\left( 2 \right)\).
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {3; - 2;1} \right),\overrightarrow b = \left( {1;2;1} \right)\). Vectơ \(\overrightarrow c = \left( {12;m;n} \right)\)là vectơ vuông góc đồng thời với hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \). Tính giá trị \(4n - 5m\).
Bảng sau đây cho biết chiều cao của các học sinh lớp 12A.

Tìm khoảng tứ phân vị cho mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A (kết quả làm tròn đến hàng phần trăm).
Để đánh giá chất lượng một loa pin điện thoại mới, người ta ghi lại thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả sau

Độ lệch chuẩn (làm tròn kết quả đến hàng phần trăm) của mẫu số liệu ghép nhóm trên là bao nhiêu?
Để thiết kế một bể cá hình hộp chữ nhật, không có nắp, có độ dài một cạnh ở đáy bằng 80 cm, thể tích 16000 cm3, người thợ dùng loại kính để sử dụng mặt bên có giá thành 80000 đồng/m2 và loại kính để làm mặt đáy có giá thành 100000 đồng/m2. Chi phí thấp nhất để hoàn thành bể cá là bao nhiêu nghìn đồng?
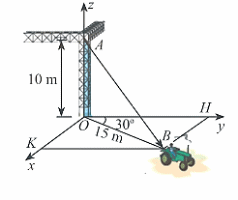
Một chiếc xe đang kéo căng sợi dây cáp \(AB\) trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ \(Oxyz\) như hình với độ dài đơn vị trên các trục tọa độ bằng 1 m. Tìm tọa độ của vectơ \(\overrightarrow {AB} \).
Một em nhỏ cân nặng \(m = 25\) kg trượt trên cầu trượt dài 4 m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 30°.
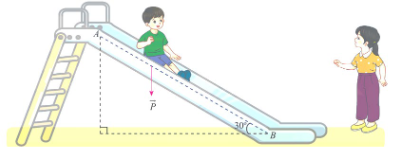
Công \(A\) (N) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P = m\overrightarrow g \) khi em nhỏ trượt hết chiều dài cầu trượt, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn là \(g = 9,8\) m/s2.