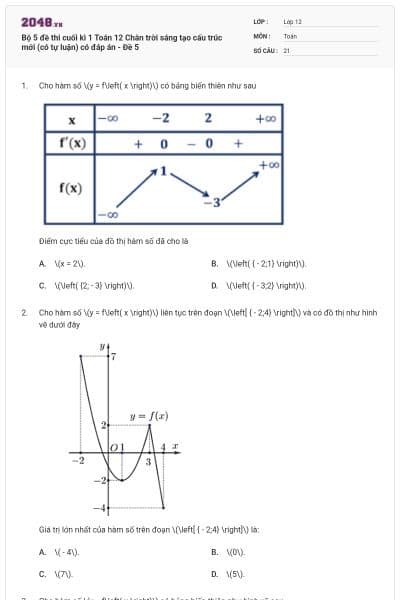
Bộ 5 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 3
21 câu hỏi
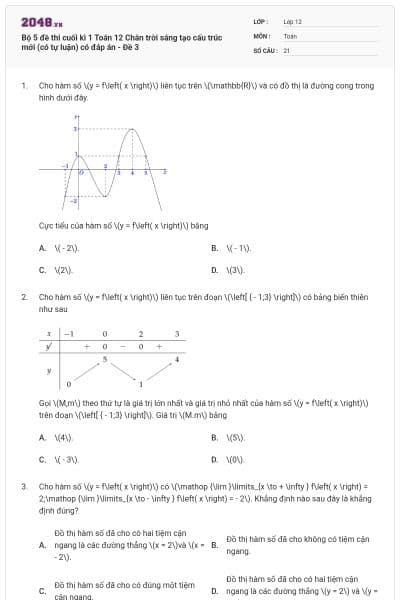
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình dưới đây.
Cực tiểu của hàm số \(y = f\left( x \right)\) bằng
\( - 2\).
\( - 1\).
\(2\).
\(3\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) có bảng biến thiên như sau
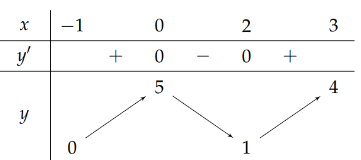
Gọi \(M,m\) theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\). Giá trị \(M.m\) bằng
\(4\).
\(5\).
\( - 3\).
\(0\).
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\). Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng \(x = 2\)và \(x = - 2\).
Đồ thị hàm số đã cho không có tiệm cận ngang.
Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng \(y = 2\) và \(y = - 2\).
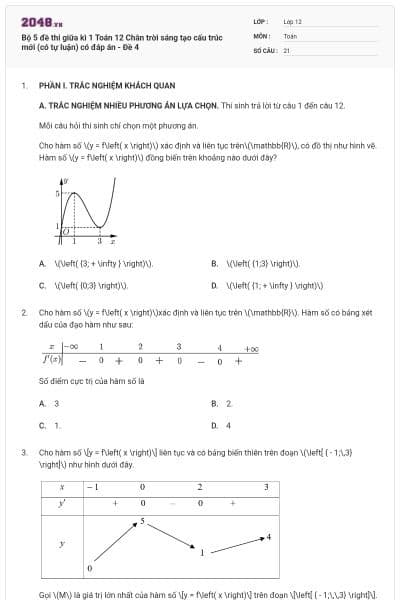
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
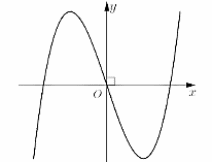
\(y = {x^3} - 3x\).
\(y = - {x^3} + 3x\).
\(y = {x^3} - 3{x^2} + 1\).
\(y = - {x^3} + 3{x^2}\).
Cho hình hộp \(ABCD.A'B'C'D'\)
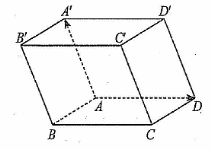
Khi đó \(\overrightarrow {AA'} + \overrightarrow {AD} \) bằng
\(\overrightarrow {AD'} \).
\(\overrightarrow {AB'} \).
\(\overrightarrow {AC'} \).
\(\overrightarrow {AC} \).
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a = \left( {3; - 1;2} \right)\). Độ dài của vectơ \(\overrightarrow a \) bằng
\(\sqrt 6 \).
\(\sqrt {14} \).
\(2\).
\(4\).
Bảng dưới thống kê khối lượng một số quả táo được lựa chọn ngẫu nhiên trong một thùng hàng

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
\(10\).
\(12\).
\(2\).
\(20\).
Chọn đáp án phù hợp để điền vào chỗ trống trong mệnh đề: “Phương sai của mẫu số liệu ghép nhóm ….”
A. Lớn hơn phương sai của mẫu số liệu gốc.
B. Xấp xỉ phương sai của mẫu số liệu gốc và được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
C. Được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
D. Lớn hơn phương sai của mẫu số liệu gốc và được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm đó.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {\left( {1 - x} \right)^2}{\left( {x + 1} \right)^3}\left( {3 - x} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ;1} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\[\left( {1;3} \right)\].
\(\left( {3; + \infty } \right)\).
Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) trên đoạn \(\left[ {0;4} \right]\). Tính tổng \(S = M + m\).
\(\frac{7}{3}\).
\(1\).
\[\frac{{10}}{3}\].
\(4\).
Cho ba điểm \(A\left( {3;1;0} \right),B\left( {2;1; - 1} \right),C\left( {x;y; - 1} \right)\). Tìm tọa độ \(C\) để tam giác \(ABC\) là tam giác vuông cân tại \(A\).
\(\left( {4;1 + \sqrt 2 ; - 1} \right);\left( {4;1 - \sqrt 2 ; - 1} \right)\).
\(\left( {4;1; - 1} \right)\).
\[\left( {2;1; - 1} \right)\].
\(\left( {2; - 1; - 1} \right)\).
Trong không gian \(Oxyz\), cho điểm \(K\left( {1;5; - 2} \right)\) và \(\overrightarrow {KH} = \left( {5;2; - 1} \right)\).Tọa độ của điểm \(H\) là
\(H\left( { - 4;3; - 1} \right)\).
\(H\left( {5;10;2} \right)\).
\[H\left( {6;7; - 3} \right)\].
\(H\left( {4; - 3;1} \right)\).
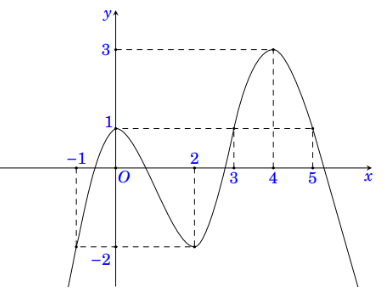
Cho hàm số đa thức bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ
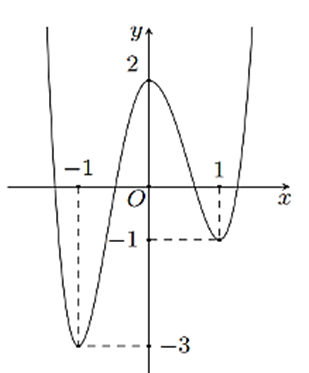
(a) \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - 3;2} \right)\).
(b) Hàm số \(y = f\left( {x + 2} \right)\) đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
(c) \(f\left( x \right)\) có hai điểm cực trị.
(d) Giá trị lớn nhất của \(f\left( x \right)\) trên đoạn \(\left[ { - 1;1} \right]\) bằng 2.
Kết quả đo cân nặng của 100 học sinh lớp 12 ở trường THPT X được cho bởi bảng sau

Khi đó:
(a) Khoảng biến thiên của mẫu số liệu ghép nhóm là 25.
(b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là 7.
(c) Phương sai của mẫu số liệu ghép nhóm bằng 28,5.
(d) Độ lệch chuẩn của mẫu số liệu ghép nhóm bằng 5.
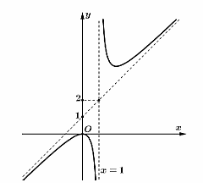
Cho hàm số \(y = \frac{{{x^2} + a}}{{x + b}}\) có đồ thị là đường cong trong hình vẽ. Tính giá trị của \(T = a + b\).
Trong một mẫu số liệu ghép nhóm ta tìm được \({Q_1} = 5;{Q_2} = 10,{Q_3} = 15\) là tứ phân vị của một mẫu số liệu trên. Tìm khoảng tứ phân vị của mẫu số liệu trên.
Cho tứ diện đều \(ABCD\) cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(CD\), \(G\) là trung điểm của \(AM\) biết \(\overrightarrow {BG} .\overrightarrow {AC} = n{a^2}\) ( \(n\) là số thập phân). Tìm \(n\) (kết quả làm tròn đến hàng phần mười).
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1;2; - 1} \right),B\left( {2; - 1;3} \right),C\left( { - 4;7;5} \right)\). Tọa độ chân đường phân giác trong góc \(B\) của tam giác \(ABC\) là \(\left( {a;b;c} \right)\). Tính tổng \(T = a + b + c\).
Một người quản lí ở một trang trại nuôi cá xác định rằng: Sau \(t\) tháng kể từ khi thả 300 con cá X với \(0 \le t \le 10\) thì khối lượng trung bình \(m\left( t \right)\) tính theo kg của một con cá X ước tính là \(m\left( t \right) = 0,45\left( {0,2 + \frac{{141}}{{155}}t - 0,05{t^2}} \right)\). Người này cũng nhận định tỉ lệ giữa số lượng cá X còn sống trong ao so với số lượng cá X thả ban đầu sau \(t\) tháng kể từ ngày thả là \(p\left( t \right) = \frac{{31}}{{31 + t}}\). Biết rằng sản lượng cá X tại một thời điểm được tính bằng tổng khối lượng của các con cá \(X\) đã thả còn sống trong ao lúc đó. Hỏi với những nhận định trên của người quản lý thì dự kiến trong tối đa 10 tháng nuôi, sản lượng cá X lớn nhất có thể đạt được là bao nhiêu?
Tại một vị trí cụ thể ở núi Bà Đen người ta đặt cố định một hệ trục tọa độ \(Oxyz\), mỗi đơn vị trên mỗi trục có độ dài bằng 1 mét. Một người đứng cố định tại vị trí \(B\left( {2;0; - 1} \right)\), quan sát một chiếc cabin cáp treo và thấy rằng cabin này xuất phát từ điểm \(A\left( { - 1;4;3} \right)\), chuyển động thẳng đều theo hướng của vectơ \(\overrightarrow u = \left( {1;2; - 2} \right)\) với vận tốc 6 m/s. Hỏi sau 5 giây kể từ lúc xuất phát khoảng cách giữa cabin và người quan sát bằng bao nhiêu mét?
Trong không gian với hệ trục tọa độ \(Oxyz\), cho tứ diện \(ABCD\) có \(A\left( {1;3; - 2} \right),B\left( { - 1; - 1;0} \right),C\left( {3;1; - 1} \right),D\left( {0;2; - 2} \right)\). Tìm tọa độ điểm \(M\) trên mặt phẳng \(\left( {Oxy} \right)\) sao cho \(f = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| + 3\left| {\overrightarrow {MD} } \right|\) đạt giá trị nhỏ nhất.