Bộ 5 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 5
21 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
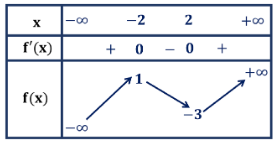
Điểm cực tiểu của đồ thị hàm số đã cho là
\(x = 2\).
\(\left( { - 2;1} \right)\).
\(\left( {2; - 3} \right)\).
\(\left( { - 3;2} \right)\).
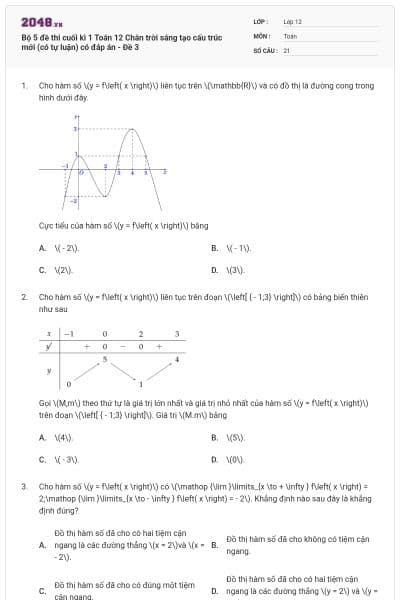
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;4} \right]\) và có đồ thị như hình vẽ dưới đây
![Cho hàm số y = f ( x ) liên tục trên đoạn [ − 2 ; 4 ] và có đồ thị như hình vẽ dưới đây Hình ảnh 1 Giá trị lớn nhất của hàm số trên đoạn [ − 2 ; 4 ] là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/blobid3-1761054351.png)
Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;4} \right]\) là:
\( - 4\).
\(0\).
\(7\).
\(5\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau
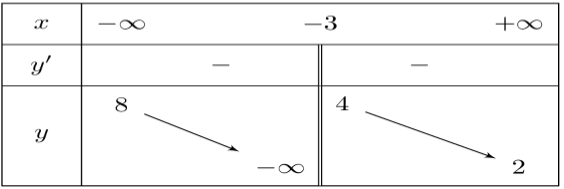
Tìm số đường tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\).
\(1\).
\(0\).
\(2\).
\(3\).
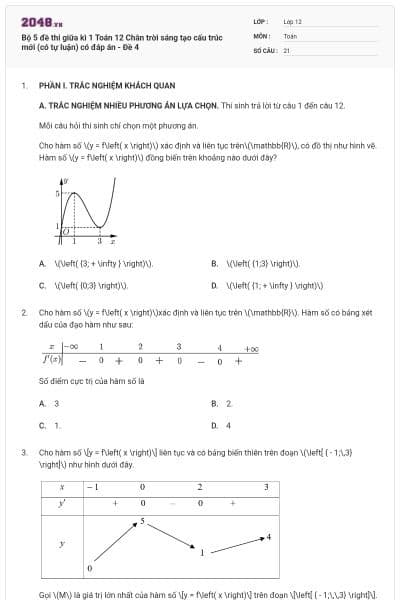
Đồ thị hàm số nào dưới đây có dạng đường cong như hình vẽ?
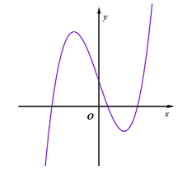
\(y = \frac{{x - 1}}{{x + 2}}\).
\(y = {x^3} - 3x + 1\).
\(y = - {x^3} + 3x + 1\).
\(y = \frac{{{x^2} + 3}}{{x + 2}}\).
Cho hình hộp \(ABCD.A'B'C'D'\), tổng \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DD'} \) là vectơ nào dưới đây?
\(\overrightarrow {BD} \).
\(\overrightarrow {DB'} \).
\(\overrightarrow {BD'} \).
\(\overrightarrow {DB} \).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là
\(\left( {3; - 2;1} \right)\).
\(\left( { - 1;2; - 3} \right)\).
\(\left( {2; - 3; - 1} \right)\).
\(\left( {1; - 2;3} \right)\).
Thời gian chạy bộ mỗi ngày trong thời gian gần đây của bạn Thuận được thống kê ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
\(20\).
\(30\).
\(15\).
\(25\).
Biết rằng phương sai của một mẫu số liệu ghép nhóm là \({s^2} = 36,36\). Độ lệch chuẩn của mẫu số liệu ghép nhóm này là
\(6,19\).
\(6,03\).
\(2,08\).
\(6,01\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 4} \right),\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
\(f\left( 0 \right) = f\left( 4 \right)\).
\(f\left( 0 \right) > f\left( 2 \right)\).
\(f\left( 4 \right) > f\left( 0 \right)\).
\(f\left( 4 \right) > f\left( 2 \right)\).
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ. Chọn mệnh đề đúng
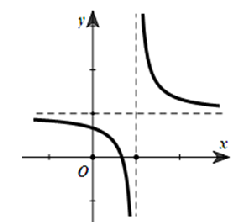
\(ac > 0\).
\(cd > 0\).
\(ab > 0\).
\(ad > bc\).
Trong không gian \(Oxyz\) cho ba điểm \(A\left( {1;2; - 1} \right),B\left( {2; - 1;3} \right),C\left( { - 3;5;1} \right)\). Tọa độ điểm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành là
\(\left( { - 2;8; - 3} \right)\).
\(\left( { - 2;2;5} \right)\).
\(\left( { - 4;8; - 5} \right)\).
\(\left( { - 4;8; - 3} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(\overrightarrow a = \left( {2; - 3; - 1} \right)\) và \(\overrightarrow b = \left( { - 2;0;4} \right)\). Vectơ \(\overrightarrow u = 2\overrightarrow a - 3\overrightarrow b \) có tọa độ là
\(\overrightarrow u = \left( { - 2; - 6;10} \right)\).
\(\overrightarrow u = \left( {10; - 6; - 14} \right)\).
\(\overrightarrow u = \left( {4; - 6; - 6} \right)\).
\(\overrightarrow u = \left( { - 2; - 6;6} \right)\).
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây
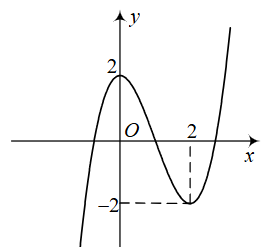
(a) Hàm số đạt cực tiểu tại \(x = 2\).
(b) Có 3 giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt.
(c) Đường cong trên là đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2\).
(d) Gọi \(M\)và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \([0;2]\) thì \(M + m = 0\)
Trong không gian \(Oxyz\), cho ba điểm \(A\left( { - 5;0;7} \right),B\left( {1;2;1} \right),C\left( {16;5; - 2} \right)\). Khi đó:
(a) \(\overrightarrow {AB} = \left( {6;2; - 6} \right)\).
(b) Góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) bằng \(158,7^\circ \).
(c) \(\left| {\overrightarrow {BC} + \overrightarrow {AB} } \right| = 5\sqrt {22} \).
(d) Điểm \(N\left( {a;b;c} \right)\) thuộc đoạn \(AB\) thỏa mãn \(NA = 3NB\). Khi đó \(a + b + c = 4,5\).
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to - {7^ - }} f\left( x \right) = - \infty \) và \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 3\). Hỏi đồ thị của hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Trong không gian \(Oxyz\), cho điểm \(M\left( {2;5;4} \right)\). Tìm tọa độ điểm \(M'\left( {a;b;c} \right)\) đối xứng với \(M\) qua mặt phẳng \(\left( {Oyz} \right)\). Tính \(a + b + c\).
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng sau:

Tổng của khoảng biến thiên và khoảng tứ phân vị của bảng số liệu trên bằng bao nhiêu?
Một nhóm vận động viên chạy marathon đã ghi lại thời gian hoàn thành cự li 42 km như sau:

Tìm phương sai của mẫu số liệu ghép nhóm này (làm tròn kết quả đến hàng phần mười).
Cho một tấm nhôm hình vuông có cạnh là 30 cm. Người ta cắt bỏ ở bốn góc của tấm nhôm đó các hình vuông bằng nhau có cạnh là \(x\) cm, sau đó gập tấm nhôm lại để tạo thành một chiếc hộp không nắp. Tìm \(x\) để thể tích chiếc hộp là lớn nhất.
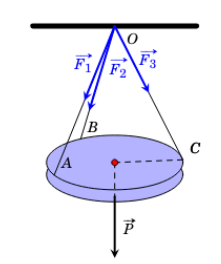
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không giãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên đèn tròn sao cho OA, OB, OC đôi một vuông góc với nhau. Biết khối lượng các sợi dây không đáng kể, các lực căng của sợi dây đặt tại điểm O là \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) có độ lớn bằng nhau và bằng 20 N. Trọng lượng của chiếc đèn đó bằng bao nhiêu newton?
Hai chiếc flycam được điều khiển cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc flycam thứ nhất nằm cách điểm xuất phát 3 m về phía nam và 2 m về phía đông, đồng thời cách mặt đất 5 m. Chiếc flycam thứ hai nằm cách điểm xuất phát 6 m về phía bắc và 6 m về phía tây, đồng thời cách mặt đất 5 m. Chọn hệ trục tọa độ \(Oxyz\) với gốc O đặt tại điểm xuất phát của hai chiếc flycam, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (coi như phẳng) có trục \(Ox\) hướng về phía nam, trục \(Oy\) hướng về phía đông và trục \(Oz\) hướng thẳng lên trời (đơn vị đo mỗi trục là mét). Trên mặt đất, người ta xác định được một vị trí sao cho tổng khoảng cách từ vị trí đó tới hai chiếc flycam ngắn nhất. Hỏi khoảng cách từ vị trí đó đến điểm xuất phát là bao nhiêu mét?
N