Bộ 5 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
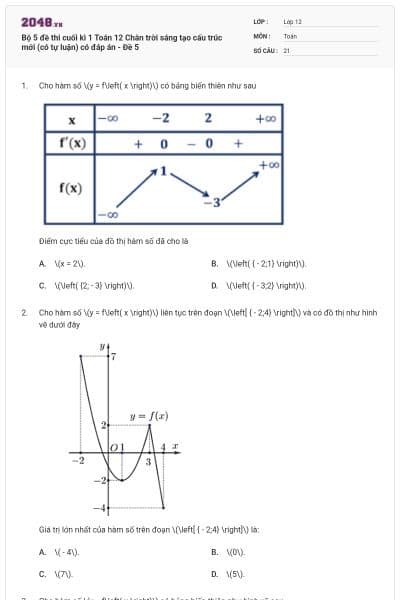
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
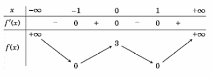
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {1; + \infty } \right)\).
\(\left( {0;1} \right)\).
\(\left( { - 1;0} \right)\).
\(\left( {0; + \infty } \right)\).
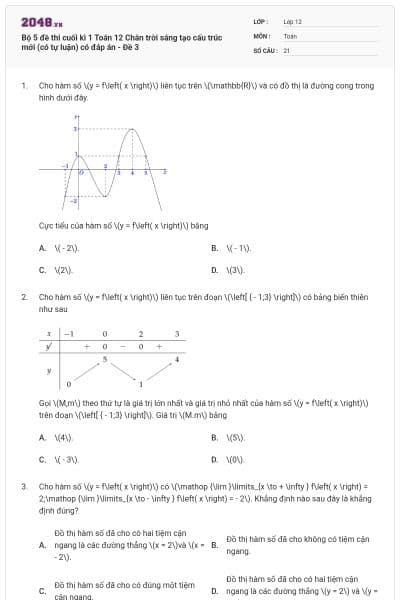
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên.
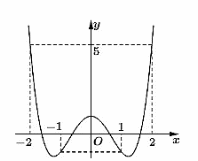
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;2} \right]\).
\(1\).
\(2\).
\(5\).
\(0\).
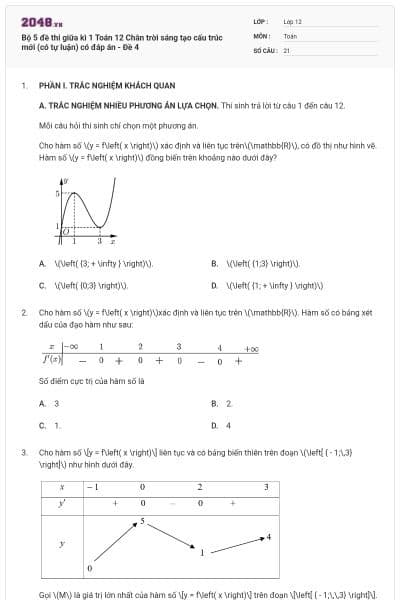
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
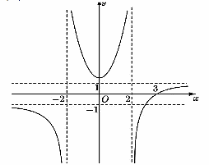
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
\(4\).
\(2\).
\(1\).
\(3\).
Đường cong trong hình là đồ thị của hàm số nào dưới đây?
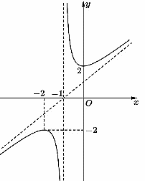
\(y = \frac{{{x^2} - 2x - 3}}{{x - 2}}\).
\(y = \frac{{{x^2} - 2x}}{{x + 1}}\).
\(y = \frac{{{x^2} + 3x}}{{x - 2}}\).
\(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Hàm số nào đồng biến trên \(\mathbb{R}\) trong các hàm số dưới đây.
\(y = {x^4}\).
\(y = {x^3} + 2x\).
\(y = {x^2} + x + 1\).
\(y = - 3x + 2\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 1}}{{2x + 4}}\) là
\(x = - 2\).
\(x = 1\).
\(y = 1\).
\(y = - 2\).
Cho hình hộp \(ABCD.A'B'C'D'\).
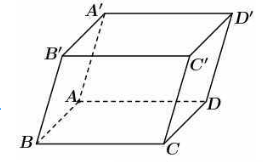
Khẳng định nào sau đây sai?
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {D'C'} } \right|\).
\(\left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {A'C'} } \right|\).
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AC'} \).
Trong không gian với hệ tọa độ \(Oxyz\), giả sử \(\overrightarrow {OM} = 2\overrightarrow i + 3\overrightarrow j - \overrightarrow k \). Khi đó tọa độ điểm \(M\) là
\(\left( { - 2;3;1} \right)\).
\(\left( {2; - 3; - 1} \right)\).
\(\left( {2;3; - 1} \right)\).
\(\left( {2;3;1} \right)\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1;2; - 3} \right)\). Hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là
\(\left( {0;2; - 3} \right)\).
\(\left( {1;0; - 3} \right)\).
\(\left( {1;2;0} \right)\).
\(\left( {1;0;0} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {2;1;0} \right)\) và \(\overrightarrow b = \left( { - 1;0;2} \right)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{2}{{25}}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{2}{5}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{2}{{25}}\).
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{2}{5}\).
Cho mẫu số liệu ghép nhóm thời gian sử dụng internet trong 1 tuần (giờ) của 20 học sinh như sau

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng
30.
29.
25.
8.
Cân nặng của một số quả mít trong một khu vườn được thống kê ở bảng sau

Hãy tính phương sai của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
18,04.
6,40.
8,72.
2,53.
Trong không gian với hệ tọa độ \(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1; - 1;0} \right),B\left( { - 2;5;3} \right),C\left( {3;4;9} \right)\).
(a) Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là \(G\left( {\frac{2}{3};\frac{4}{3};4} \right)\).
(b) Đoạn \(AB\) cắt mặt phẳng \(\left( {Oxz} \right)\) tại điểm \(M\left( {a;b;c} \right)\). Khi đó \(a + b + c = 6\).
(c) Tọa độ vectơ \(\overrightarrow {AB} = \left( {3; - 6; - 3} \right)\).
(d) Với điểm \(D\left( {6; - 2;6} \right)\) thì tứ giác \(ABCD\) là hình bình hành.
Kết quả đo chiều cao (đơn vị: cm) của 25 học sinh nam lớp 12 ở một trường THPT được biểu diễn bởi mẫu số liệu ghép nhóm ở bảng sau:

( a) Khoảng biến thiên của mẫu số liệu ghép nhóm là \(R = 5\) cm.
(b) Giá trị đại diện của nhóm \(\left[ {155;160} \right)\) là 158.
(c) Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là \(s = 29,84\).
(d) Số trung bình của mẫu số liệu ghép nhóm là 167,9.
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ bên dưới. Gọi \(I\left( {m;n} \right)\) là tâm đối xứng của đồ thị hàm số đã cho. Giá trị của \(m + n\) bằng bao nhiêu?
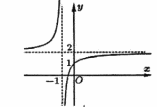
Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {1; - 3;1} \right),\overrightarrow b = \left( { - 1;1;2} \right)\). Giá trị của tích vô hướng \(\overrightarrow a .\overrightarrow b \) bằng bao nhiêu?
Cho tứ diện đều \(ABCD\) có cạnh bằng 12. Biết độ dài của \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \) bằng \(a\sqrt 6 \). Tìm \(a\).
Điều tra về độ tuổi của 200 cư dân trong một khu phố (đơn vị: độ tuổi) được kết quả cho trong bảng sau:

Tìm khoảng tứ phân vị của mẫu số liệu trên (kết quả làm tròn đến hàng phần chục).
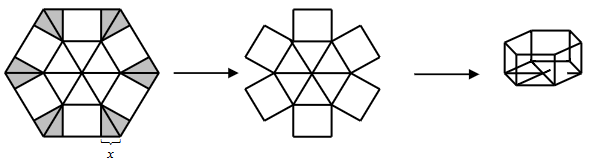
Cho một tấm nhôm hình lục giác đều cạnh 100 cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng \(x\) cm (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm \(x\) để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (đơn vị cm).
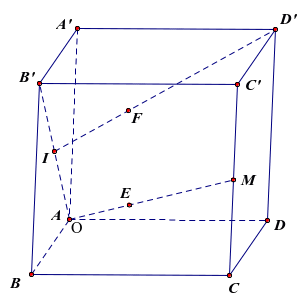
Bạn An đang nằm nghe nhạc trong phòng hình hộp chữ nhật, sàn nhà là hình vuông cạnh bằng 4 m, chiều cao của phòng là 3,2 m và phát hiện ra hai con nhện đang chăng tơ trong căn phòng của An, hai con nhện luôn di chuyển trên hai đường thẳng khác nhau. Giả sử căn phòng được mô hình hóa là hình hộp chữ nhật \(ABCD.A'B'C'D'\) với \(ABCD\) là nền phòng của An thì con nhện thứ nhất được coi như điểm \(E\)di chuyển trên đường dây tơ nối từ đỉnh \(A\) đến trung điểm \(M\) của \(CC'\), còn con nhện thứ hai được coi như điểm \(F\) di chuyển trên đường dây tơ nối từ \(D'\) đến tâm \(I\) của mặt \(ABB'A'\). Tính khoảng cách giữa hai con nhện khi đường thẳng đi qua hai con nhện vuông góc với trần nhà (đơn vị mét).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) đạt cực trị tại các điểm \({x_1};{x_2}\) với \({x_1} \in \left( { - 1;0} \right),{x_2} \in \left( {1;2} \right)\). Biết hàm số đồng biến trên khoảng \(\left( {{x_1};{x_2}} \right)\). Đồ thì hàm số cắt trục tung tại điểm có tung độ âm. Xác định dấu của các hệ số \(a,b,c,d\).