Bộ 5 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 2
21 câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau
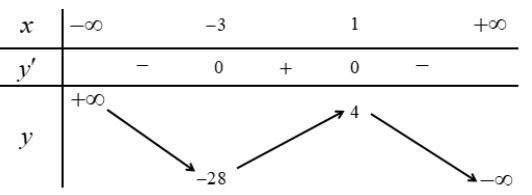
Hàm số đã cho nghịch biến trên khoảng nào sau đây
\(\left( { - 3; + \infty } \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - 3;1} \right)\).
\(\left( { - \infty ;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
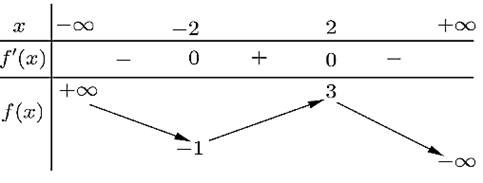
Trên khoảng \(\left( {0; + \infty } \right)\) giá trị lớn nhất của hàm số đã cho bằng
\(3\).
\( - 2\).
\( - 1\).
\(2\).
Hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
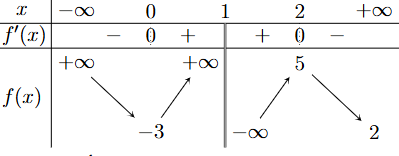
Đồ thị hàm số đã cho có tiệm cận ngang là đường thẳng nào sau đây?
\(y = 1\).
\(y = - 3\).
\(y = 5\).
\(y = 2\).
Đồ thị hàm số nào sau đây có dạng như đường cong trong hình vẽ?
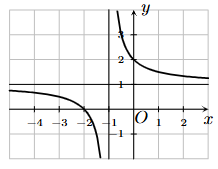
\(y = {x^3} - 3x + 1\).
\(y = \frac{{x - 2}}{{x + 1}}\).
\(y = 2{x^4} + {x^2} + 1\).
\(y = \frac{{x + 2}}{{x + 1}}\).
Cho hình chóp \(S.ABCD\), khi đó \(\overrightarrow {AB} + \overrightarrow {BS} + \overrightarrow {SA} \) bằng
\(\overrightarrow {AB} \).
\(\overrightarrow {BS} \).
\(\overrightarrow {SA} \).
\(\overrightarrow 0 \).
Trong hệ trục tọa độ \(Oxyz\), cho \(\overrightarrow u = \overrightarrow i - 3\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow u \) là
\(\left( {1; - 1;3} \right)\).
\(\left( {1; - 3;0} \right)\).
\(\left( {0;2; - 3} \right)\).
\(\left( {1;0; - 3} \right)\).
Trong hệ trục tọa độ \(Oxyz\), xác định vectơ cùng phương với vectơ \(\overrightarrow n = \left( {1;1;0} \right)\).
\(\overrightarrow u = \left( {2;0;2} \right)\).
\(\overrightarrow u = \left( {0;2;2} \right)\).
\(\overrightarrow u = \left( {2;2;2} \right)\).
\(\overrightarrow u = \left( {2;2;0} \right)\).
Trong hệ trục tọa độ \(Oxyz\), cho \(\overrightarrow a = \left( {2; - 3;3} \right),\overrightarrow b = \left( {0;2; - 1} \right)\). Tìm tọa độ của vectơ \(\overrightarrow a - \overrightarrow b \).
\(\left( {2; - 1;2} \right)\).
\(\left( { - 2;5; - 4} \right)\).
\(\left( {2;1;2} \right)\).
\(\left( {2; - 5;4} \right)\).
Trong hệ trục tọa độ \(Oxyz\), tọa độ trung điểm của đoạn \(AB\) với \(A\left( {1;0; - 3} \right)\) và \(B\left( { - 1;2;1} \right)\) là
\(\left( {1; - 1; - 2} \right)\).
\(\left( {2; - 2; - 4} \right)\).
\(\left( {0;2; - 2} \right)\).
\(\left( {0;1; - 1} \right)\).
Trong hệ trục tọa độ \(Oxyz\), xác định tọa độ vectơ \(\overrightarrow {AB} \) với \(A\left( {1; - 1;0} \right)\) và \(B\left( {2; - 2;1} \right)\).
\(\sqrt {19} \).
\(\sqrt 3 \).
\(\left( {3; - 3;1} \right)\).
\(\left( {1; - 1;1} \right)\).
Khi điều tra cân nặng của 50 bé trai 6 tuổi ở một địa phương, người ta thống kê được kết quả như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên bằng
\(8\).
\(18\).
\(26\).
\(2\).
Một mẫu số liệu ghép nhóm có các tứ phân vị là \({Q_1} = 51;{Q_2} = 58;{Q_3} = 70\). Khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu ghép nhóm đó bằng
\(12\).
\(19\).
\(21\).
\(17\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 2a,AD = 3a,A'A = 4a\).
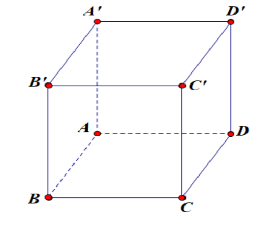
( a) \(\overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC'} \).
(b) Gọi \(G\) là trọng tâm tam giác \(D'DC\). Khi đó \(\overrightarrow {AG} .\overrightarrow {DB} = - \frac{{23}}{3}{a^2}\).
(c) \(\left| {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {CC'} } \right| = a\sqrt {29} \).
( d) \(\overrightarrow {AA'} .\overrightarrow {AD} = 12{a^2}\).
Số giờ sử dụng smartphone trong 1 ngày nghỉ của học sinh lớp 12A được thống kê trong bảng sau

( a) Khoảng biến thiên của mẫu số liệu trên bằng 6.
(b) Khoảng tứ phân vị của mẫu số liệu trên bằng 5.
(c) Giá trị trung bình của mẫu số liệu trên bằng \(\frac{{226}}{{45}}\).
(d) Độ lệch chuẩn của mẫu số liệu trên bằng \(\frac{{2\sqrt {730} }}{{45}}\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right){\left( {x + 2} \right)^2}{\left( {x - 3} \right)^3}\) trên \(\mathbb{R}\). Hàm số đã cho có bao nhiêu điểm cực trị?
Trong không gian \(Oxyz\)cho ba điểm \(A\left( {3;2; - 1} \right),B\left( { - 1; - x;1} \right),C\left( {7; - 1;y} \right)\). Khi \(A,B,C\) thẳng hàng thì giá trị biểu thức \(x + y\) bằng bao nhiêu?
Giả sử giá trị nhỏ nhất của hàm số \(y = \frac{{\ln x}}{x}\) trên đoạn \(\left[ {2;3} \right]\) bằng \(\frac{{a\ln 2}}{b}\) với \(a,b\) nguyên tố cùng nhau. Tính \(a - 5b\).
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực A, B cho kết quả như sau:

Tính tổng độ lệch chuẩn cho các mẫu số liệu về tiền lãi của các nhà đầu tư vào hai lĩnh vực A và B (làm tròn kết quả cuối cùng đến hàng phần mười).
Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) mét vải lụa ( \(1 \le x \le 18\)).Tổng chi phí sản xuất \(x\) mét vải lụa (tính bằng nghìn đồng) cho bởi hàm chi phí \(C\left( x \right) = {x^3} - 3{x^2} - 20x + 500\).
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi \(B\left( x \right)\) là số tiền bán được và \(L\left( x \right)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa. Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày bao nhiêu mét vải lụa để thu được lợi nhuận tối đa. Hãy tính lợi nhuận tối đa đó.
Trong hệ trục tọa độ \(Oxyz\), cho tam giác \(ABC\) vuông tại \(A\) thuộc tia \(Ox\), \(B\) thuộc tia \(Oy\) và trọng tâm tam giác \(ABC\) thuộc tia \(Oz\). Tính tỉ số \(\frac{{OA}}{{OB}}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ.
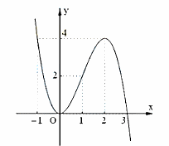
Phương trình \(f\left( x \right) = f\left( 3 \right)\) có bao nhiêu nghiệm?