Bộ 5 đề thi giữa kì 1 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
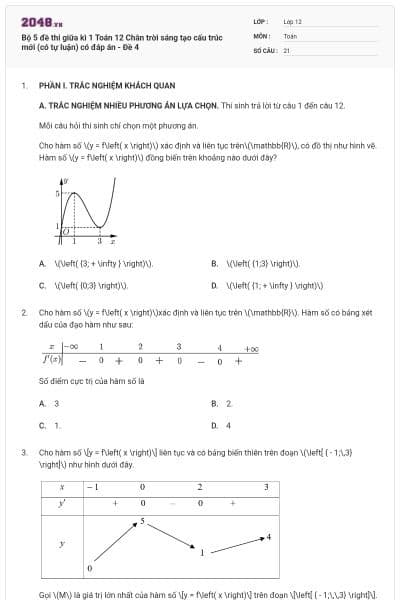
Cho hàm số có đồ thị như hình vẽ dưới đây.
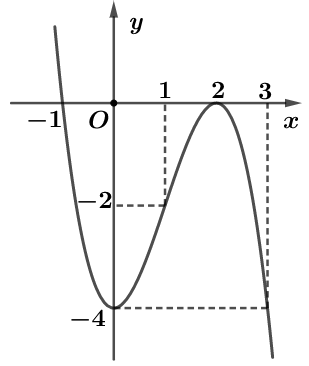
Hàm số đồng biến trên khoảng nào?
\(\left( {2; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
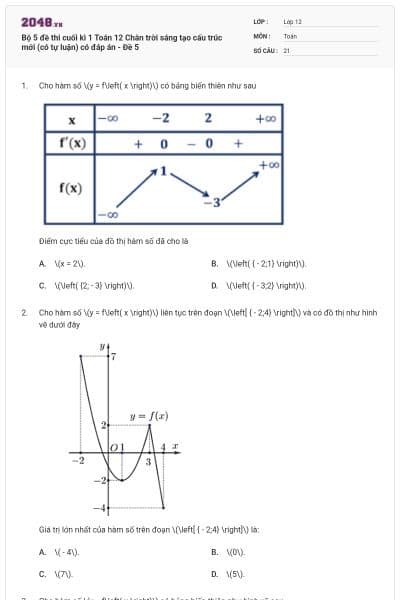
Cho hàm số có bảng biến thiên như sau:
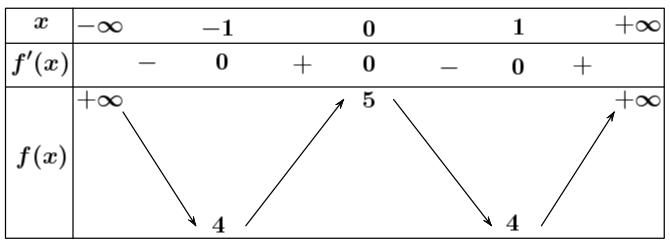
Giá trị cực đại của hàm số đã cho bằng
0.
5.
4.
-1.
Cho hàm số liên tục trên và có bảng biến thiên như hình dưới đây.
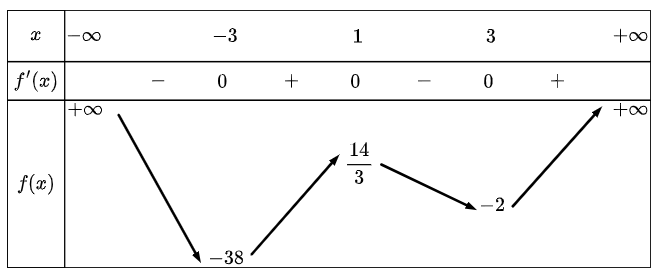
Khi đó giá trị nhỏ nhất của hàm số trên đoạn bằng bao nhiêu?
-38
-2
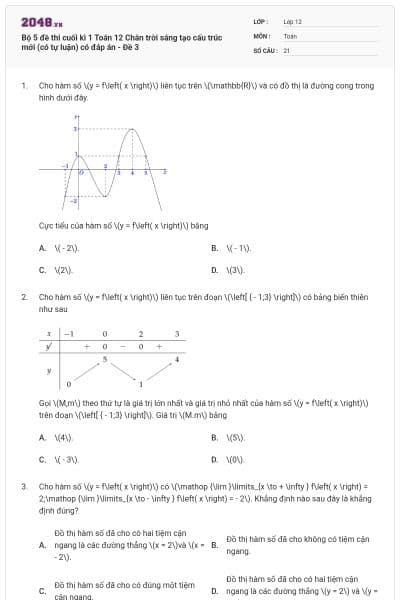
Cho hàm số ) có đồ thị là đường cong như hình dưới đây.

Đồ thị hàm số đã cho có đường tiệm cận đứng là
\(y = - 1\).
\(x = \frac{1}{3}\).
\(y = - \frac{1}{3}\).
\(x = - \frac{1}{3}\)
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2 - x}}{{2x + 1}}\) có phương trình là:
\(x = - \frac{1}{2}\).
\(y = 1\).
\(y = - \frac{1}{2}\).
\(x = 2\)
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình vẽ.
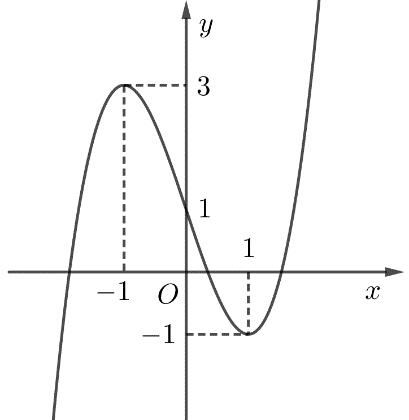
Đồ thị hàm số đã cho cắt trục tung tại điểm có tọa độ
\(\left( { - 1;\;3} \right)\).
\(\left( {1;\;0} \right)\).
\(\left( {1;\; - 1} \right)\).
\(\left( {0;\;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có bảng biến thiên như sau
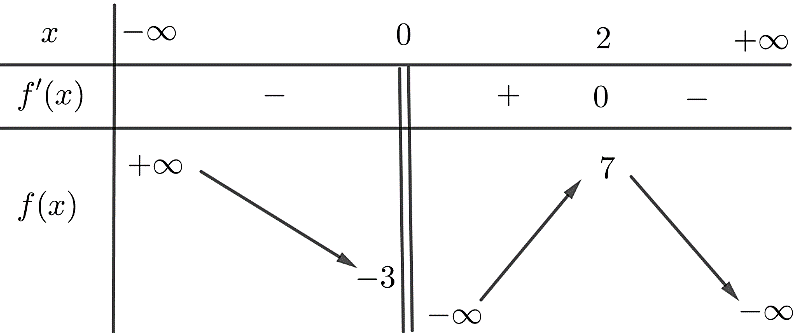
Số nghiệm của phương trình \(\frac{1}{3}f\left( x \right) + 1 = 0\) là
\(1.\)
\(3.\)
\(0.\)
\(2.\)
Cho tứ diện ABCD, gọi I là trung điểm của đoạn thẳng AB.
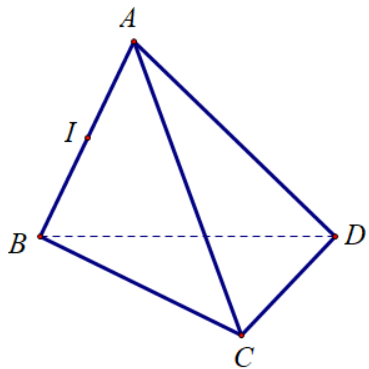
Vectơ \(\overrightarrow {AI} \) cùng hướng với vectơ nào sau đây?
\(\overrightarrow {CD} \).
\(\overrightarrow {AB} \).
\(\overrightarrow {CI} \).
\(\overrightarrow {BI} \).
Chohình lập phương\[ABCD.A'B'C'D'\].
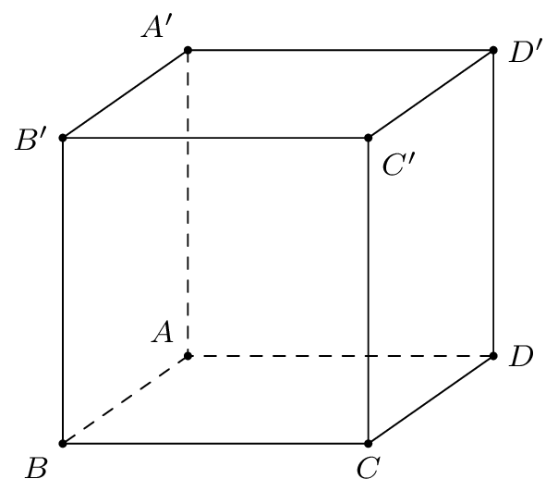
Số đo góc \[\left( {\overrightarrow {BC} ,\overrightarrow {B'D'} } \right)\] bằng
45
90
60
135
Hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right)\left( {{x^2} - 1} \right)\). Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng
\(\left( {1;2} \right)\).
\(\left( { - 2; - 1} \right)\).
\(\left( { - 1;0} \right)\).
\(\left( {0;1} \right)\).
Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
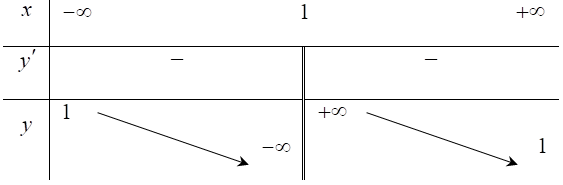
Bảng biến thiên trên của hàm số nào trong các hàm số sau?
\(y = \frac{{ - x + 2}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x + 1}}\).
\(y = \frac{{x - 3}}{{x - 1}}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh 2 (tham khảo hình vẽ dưới).
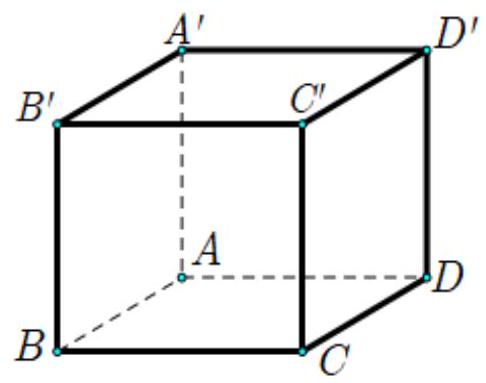
Độ dài vectơ \(\vec u = \overrightarrow {A'C'} - \overrightarrow {A'A} \) bằng
2
2
2
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).
a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).
c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).
d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = 1\) và \(BC = \sqrt 2 \).
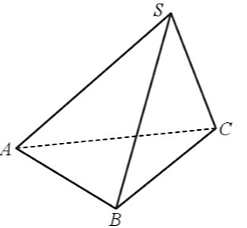
a)\(\overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {SC} \).
b)\(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = \sqrt 2 \).
c)\(\overrightarrow {SC} \cdot \overrightarrow {AB} = \frac{1}{2}\).
d) \(\cos \left( {\overrightarrow {SC} ,\,\overrightarrow {AB} } \right) = \frac{1}{2}\).
C. TRẢ LỜI NGẮN
Trong một thí nghiệm y học, người ta cấy \(900\) con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo giời gian bởi công thức: \(N\left( t \right) = 900 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó \(t\) là thời gian tính bằng giây \(\left( {t \ge 0} \right)\). Trong khoảng thời gian \(\left( {a;b} \right)\) từ lúc nuôi cấy thì số lượng vi khuẩn sẽ tăng lên. Tính \(3a + \,2b\).
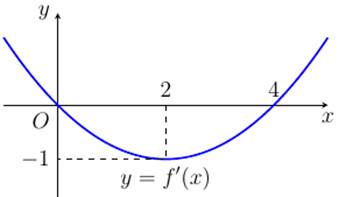
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị \(\left( C \right)\). Biết \(y = f'\left( x \right)\) có đồ thị như hình vẽ và tâm đối xứng của đồ thị \(\left( C \right)\) thuộc trục hoành. Tính khoảng cách giữa hai điểm cực trị của đồ thị \(\left( C \right)\). (Quy tròn kết quả đến hàng phần trăm).
Gọi \[m\], \[M\] lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \[f\left( x \right) = 2x + \cos \frac{{\pi x}}{2}\] trên đoạn \(\left[ { - 2\,;\,2} \right]\). Tính giá trị của biểu thức\(m + M\).
Cho hình chóp \(S.ABC\). Trên cạnh \(SA\), lấy điểm \(M\) sao cho \(SM = 2AM\). Trên cạnh \(BC\), lấy điểm \(N\) sao cho \(CN = 2BN\). Khi đó\(\overrightarrow {MN} = \frac{a}{b}\overrightarrow {AB} + \frac{c}{b}\overrightarrow {SC} \) với \(\,\frac{a}{b},\frac{c}{b}\)là các phân số tối giản. Tổng \(a + b + c\) bằng bao nhiêu?
PHẦN II. TỰ LUẬN
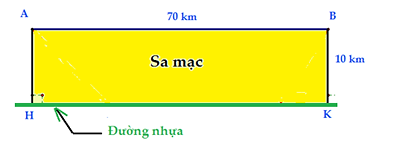
Một người đang ở tại điểm A trên sa mạc. Ông ta muốn đến điểm B và cách A một đoạn là 70 km. Trong sa mạc thì xe ông ta chỉ có thể di chuyển với vận tốc 30 km/h. Ông ấy phải đến được điểm B trong 2 giờ. Biết rằng có một con đường nhựa HK song song với AB và cách AB một đoạn 10 km. Trên đường nhựa này thì xe ông ấy có thể di chuyển với vận tốc 50 km/h . Để đến B sớm nhất (đảm bảo trong khung giờ cho phép) thì ông phải đi theo con đường nào?
Người ta bơm xăng vào bình xăng của một xe ô tô. Biết rằng thể tích \(V\) (tính theo lít) của lượng xăng trong bình xăng được tính theo thời gian bơm xăng \(t\) (phút) được cho bởi công thức:
\(V\left( t \right) = 300\left( {{t^2} - {t^3}} \right) + 4,5\) với \(0 \le t \le 0,5\).
Gọi \(V\prime \left( t \right)\) là tốc độ tăng thể tích tại thời điểm \(t\) với \(0 \le t \le 0,5\). Biết \(1\) lít xăng có giá là \(21\,000\) đồng.
a) Biết rằng sau khi bơm \(30\) giây thì bình xăng đầy, hỏi người mua phải trả bao nhiêu tiền?
b) Khi xăng chảy vào bình xăng thì tốc độ tăng thể tích là lớn nhất vào thời điểm nào?
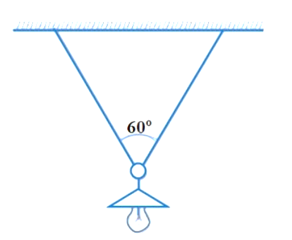
Người ta treo một bóng đèn có khối lượng m = 1 kg bằng cách luồn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt trên trần nhà. Hai nửa sợi dây có chiều dài bằng nhau và hợp với nhau một góc bằng 60°. Tính lực căng của mỗi nửa sợi dây, lấy g = 10 m/s2.