Bộ 5 đề thi giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Đề 04
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các câu sau, câu nào là mệnh đề?
Đi ngủ đi!
Trung Quốc là nước đông dân nhất thế giới.
Bạn học ở trường nào?
Không được làm việc riêng trong giờ học.
Cách viết nào sau đây là sai?
\(\left( {0; + \infty } \right) = \left\{ {x \in \mathbb{R}|x > 0} \right\}\).
\(\left[ {0;5} \right] = \left\{ {x \in \mathbb{R}|0 \le x \le 5} \right\}\).
\(\left( {0;5} \right) = \left\{ {x \in \mathbb{R}|0 < x < 5} \right\}\).
\(\left[ { - 1;5} \right) = \left\{ { - 1;0;1;2;3;4} \right\}\).
Cho các tập hợp \(A = \left\{ {x \in \mathbb{R}\,\left| {\,\,{x^2} - 9 \ge 0} \right.} \right\}\) và \(B = \left( {0\,;\,3} \right)\). Biết rằng \(A \cup B = \left( { - \infty \,;\,a} \right] \cup \left( {b\,;\, + \infty } \right)\). Tính giá trị của biểu thức \(a + b\).
\(a + b = 0\).
\(a + b = - 3\).
\(a + b = 3\).
\(a + b = 6\).
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(2x - 5y + 3z \le 0\).
\(2x + 3y < 5\).
\(3{x^2} + 2x - 4 > 0\).
\(2{x^2} + 5y > 3\).
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 > 0\end{array} \right.\]. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
\(N\left( { - 1\,;1} \right)\).
\(Q\left( { - 1\,;0} \right)\).
\(P\left( {1\,; - 3} \right)\).
\(M\left( {0\,;1} \right)\).
Miền nghiệm của bất phương trình \[x - 2 + 2\left( {y - 1} \right) > 2x + 4\] chứa điểm nào sau đây?
\(A\left( {1\,\,;\,\,1} \right).\)
\(B\left( {1\,\,;\,\,5} \right).\)
\(C\left( {4\,\,;\,\,3} \right).\)
\(D\left( {0\,\,;\,\,4} \right).\)
Tập xác định của hàm số \(y = \sqrt {x - 7} \) là
\(\left( { - \infty ;7} \right].\)
\(\left( { - \infty ;7} \right).\)
\(\left( {7; + \infty } \right).\)
\(\left[ {7; + \infty } \right).\)
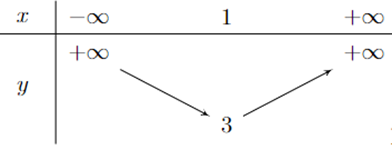
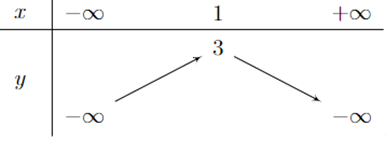
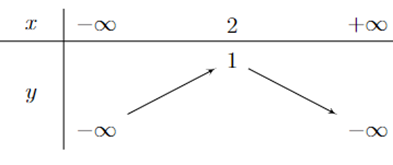
Bảng biến thiên của hàm số \(y = - 2{x^2} + 4x + 1\) là bảng nào sau đây?
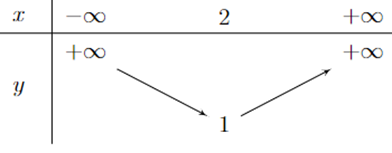
Parabol \(y = a{x^2} + bx + c\) đi qua \(A\left( {8;0} \right)\) và có đỉnh \(I\left( {6; - 12} \right)\). Khi đó tích \(a.b.c\) bằng
\( - 10368.\)
\(10368.\)
\(6912.\)
\( - 6912.\)
Góc nào dưới đây có côsin là một số âm?
\(75^\circ \).
\(23^\circ \).
\(125^\circ \).
\(82^\circ \).
Cho tam giác ABC có nửa chu vi bằng 6 và bán kính đường tròn nội tiếp tam giác bằng 1. Diện tích tam giác ABC bằng
\[12\].
\[3\].
\[6\].
\[24\].
Biết rằng \[\cos \alpha = \frac{1}{3}\]. Giá trị của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) là
\[\frac{1}{3}\].
\[\frac{{10}}{9}\].
\[\frac{{11}}{9}\].
\[\frac{4}{3}\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét tính đúng sai của mỗi câu sau:
a) A: “Năm 2010 là năm nhuận”.
b) Cho tập hợp \(A = \left\{ {n \in \mathbb{N}|2n + 1 \le 17} \right\}\), \(B = \left\{ {n \in \mathbb{N}|{n^2} \le 25} \right\}\). Tập hợp \(A \cap B\) có 6 phần tử.
c) H: “\(\sqrt 2 \) là số vô tỉ” có mệnh đề phủ định là \(\overline H :\) “\(\sqrt 2 \)là số hữu tỉ”.
d) Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Suy ra có 1 học sinh chỉ giỏi môn Lý.
Bác An dự định trồng hai loại cây ăn trái là mít và xoài trong nông trại rộng 100 hecta. Biết mỗi hecta trồng mít cần 20 công chăm sóc và thu lại lợi nhuận 150 triệu đồng, mỗi hecta trồng xoài cần 40 công chăm sóc và thu lại lợi nhuận 180 triệu đồng. Biết rằng tổng số công cần dùng không được vượt quá 2 800 công. Gọi \(x,y\) (hecta) lần lượt là diện tích đất dùng để trồng mít và xoài. Xét tính đúng sai của các phát biểu sau.
a) \(x + y \le 100\).
b) \(x + 2y \le 140\).
c) Tổng lợi nhuận thu được là \(E = 150x + 180y\) (triệu đồng).
d) Lợi nhuận thu được lớn nhất là 16 tỷ đồng.
Quan sát đồ thị hàm số bậc hai \(y = f\left( x \right)\) ở hình bên dưới
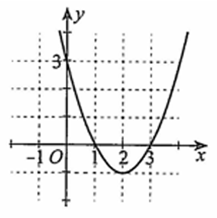
Các mệnh đề sau đúng hay sai?
a) \(a > 0\).
b) Tọa độ đỉnh \(I\left( {2; - 1} \right)\), trục đối xứng \(x = 2\).
c) \(x\) thuộc các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\) thì \(f\left( x \right) > 0\).
d) Đường thẳng \(y = 4\) cắt đồ thị hàm số tại hai điểm phân biệt có hoành độ dương.
Cho tam giác ABC có \(AB = 8,AC = 5,\widehat A = 60^\circ \). Các câu sau đúng hay sai?
a) Diện tích tam giác ABC bằng \(S = \frac{1}{2}AB.AC.\sin A\).
b) Độ dài cạnh \(BC = 4\sqrt 3 \).
c) Khoảng cách từ B đến AC bằng \(4\sqrt 3 \).
d) Điểm M thuộc cạnh BC sao cho \(BM = 5\), khi đó \(AM\) bằng \(\sqrt {46} \).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Bạn A Súa thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: 14 ngày có mưa, 15 ngày có sương mù, trong đó 10 ngày có cả mưa và sương mù. Hỏi trong tháng 3 đó có bao nhiêu ngày không có mưa và không có sương mù.
Một gian hàng trưng bày bàn và ghế rộng 60 m2. Diện tích để kê một chiếc ghế là 0,5 m2, một chiếc bàn là 1,2 m2. Gọi \(x\) là số chiếc ghế, \(y\) là số chiếc bàn được kê. Biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m2. Giả sử gian hàng đã kê 10 chiếc bàn thì phần diện tích cho phép còn lại có thể kê được nhiều nhất bao nhiêu chiếc ghế?
Bác Ba có một mảnh đất rộng \[6\] ha. Bác dự tính trồng cà chua và ngô cho mùa vụ sắp tới. Nếu trồng cà chua thì bác Ba cần \[20\] ngày để trồng một ha. Nếu trồng ngô thì bác Ba cần \[10\] ngày để trồng một ha. Biết rằng mỗi ha cà chua sau thu hoạch bán được \[50\] triệu đồng, mỗi ha ngô sau thu hoạch bán được \[30\] triệu đồng và bác Ba chỉ còn \[100\] ngày để canh tác cho kịp mùa vụ. Giả sử bác Ba trồng \[x\] ha cà chua và \[y\] ha ngô. Số tiền nhiều nhất mà bác Ba có thể thu được sau mùa vụ này là bao nhiêu triệu đồng?
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu triệu đồng để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
Tính giá trị biểu thức
\(A = {\cos ^2}15^\circ + {\cos ^2}25^\circ + {\cos ^2}35^\circ + {\cos ^2}45^\circ + {\sin ^2}15^\circ + {\sin ^2}25^\circ + {\sin ^2}35^\circ \).
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ so với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách \(AB = 40\;{\rm{m}}\), \(\widehat {CAB} = 45^\circ \), \(\widehat {CBA} = 70^\circ \). Vậy sau khi đo đạc và tính toán khoảng cách AC bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?