Bộ 5 đề thi giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Đề 03
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các câu sau, câu nào không phải là mệnh đề?
Buồn ngủ quá!
Hình thoi có hai đường chéo vuông góc với nhau.
8 là số chính phương.
Hà Nội là thủ đô của Việt Nam
Cho tập hợp \(X = \left\{ {0;2;5} \right\}\). Tập hợp nào dưới đây không phải là tập con của tập hợp \(X\)?
\(\emptyset \).
\(\left\{ 2 \right\}\).
\(\left\{ {0;2;5} \right\}\).
\(\left\{ {0;1;2} \right\}\).
Cho \(A = \left\{ {x \in \mathbb{N}|\left( {2x - {x^2}} \right)\left( {2{x^2} - 3x - 2} \right) = 0} \right\}\) và \(B = \left\{ {n \in \mathbb{N}*|3 < {n^2} < 30} \right\}\). Khi đó tập hợp \(A \cap B\) bằng
\(\left\{ {2;4} \right\}\).
\(\left\{ 2 \right\}\).
\(\left\{ {4;5} \right\}\).
\(\left\{ 3 \right\}\).
Cặp số \(\left( {{x_0};{y_0}} \right)\) nào là nghiệm của bất phương trình \( - 3x + 5y \le 6\).
\(\left( {{x_0};{y_0}} \right) = \left( {2;8} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( { - 10; - 3} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( {3;3} \right)\).
\(\left( {{x_0};{y_0}} \right) = \left( {0;2} \right)\).
Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l} - 2x \le 0\\5x - 2y < 0\end{array} \right.\) .
\(\left\{ \begin{array}{l}3y \ge 0\\x - y \ge 0\end{array} \right.\).
\(\left\{ \begin{array}{l}4x - y \ge 0\\ - x - 3y < 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \ge 0\\2x - 2{y^2} \ge 0\end{array} \right.\).
Khẳng định nào dưới đây là khẳng định đúng?
Cho bất phương trình \(3 - 3y > 0\) có miền nghiệm là nửa mặt phẳng bờ \(3 - 3y = 0\) chứa O (kể cả bờ).
Cho bất phương trình \(2x + y > 1\) có miền nghiệm là nửa mặt phẳng bờ \(2x + y - 1 = 0\) chứa O (không chứa bờ).
Cho bất phương trình \( - 2x + y + 1 \le 0\) có miền nghiệm là nửa mặt phẳng bờ \( - 2x + y + 1 = 0\) chứa O.
Cho bất phương trình \(2x - 3y + 5 \ge 0\) có miền nghiệm là nửa mặt phẳng bờ \(2x - 3y + 5 = 0\) chứa O (kể cả bờ).
Cho hàm số \(y = {x^2} + x - 2\). Giá trị của hàm số tại \(x = 2\) là
2.
−2.
4.
−4.
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị \(\left( P \right)\) như hình vẽ.
Khẳng định nào sau đây là sai?
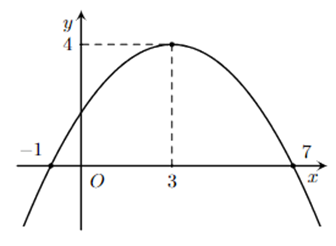
Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\).
\(\left( P \right)\) có đỉnh là \(I\left( {3;4} \right)\).
\(\left( P \right)\) cắt trục tung tại điểm có tung độ bằng 4.
\(\left( P \right)\) cắt trục hoành tại hai điểm phân biệt.
Xác định parabol (P): \(y = a{x^2} + bx + c\) biết \(\left( P \right)\) có giá trị lớn nhất bằng 3 tại \(x = 2\) và cắt trục \(Ox\) tại điểm có hoành độ bằng 1.
\(y = - {x^2} + 4x - 3\) .
\(y = {x^2} - 4x + 7\).
\(y = 2{x^2} - 12x + 20\).
\(y = - 3{x^2} + 12x - 9\).
Giá trị của \(\cos 30^\circ + \sin 60^\circ \) bằng bao nhiêu?
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\sqrt 3 \).
\(1\).
Chọn công thức đúng trong các đáp án sau.
\(S = \frac{1}{2}bc\sin A\,.\)
\(S = \frac{1}{2}ac\sin A\,.\)
\(S = \frac{1}{2}bc\sin B\,.\)
\(S = \frac{1}{2}bc\sin B\,.\)
Một tam giác có ba cạnh là \(52,56,60.\) Bán kính đường tròn ngoại tiếp tam giác là:
\(\frac{{65}}{8}.\)
\(40.\)
\(32,5.\)
\(\frac{{65}}{4}.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét tính đúng sai của các câu sau
a) Phương trình \({x^2} - 3x + 8 = 0\) có nghiệm.
b) Cho hai tập hợp \(A = \left\{ {a;c;d;e;f} \right\}\) và \(B = \left\{ {b;c;d;e;g;h} \right\}\). Khi đó \(A \subset B\).
c) \(\forall x \in \mathbb{R},{x^2} > 0\).
d) Kí hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khi đó \(G\backslash T = \emptyset \).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 1 \ge 0\\2x + y - 3 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) (I). Các câu sau đúng hay sai?
a) Đây là hệ bất phương trình bậc nhất hai ẩn.
b) \(\left( {3;2} \right)\) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình trên là một miền tứ giác.
d) \(x = 1;y = 0\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị nhỏ nhất.
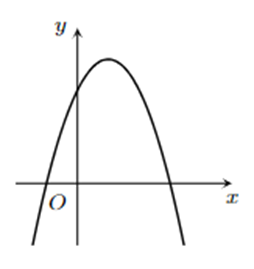
Cho hàm số \(y = a{x^2} + bx + c\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình vẽ bên.
Khẳng định sau đây đúng hay sai?
a) Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
b) Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
c) \(c > 0\).
d) \(a < 0;b > 0\).
Cho tam giác \(ABC\) có \(b = 7{\rm{cm}}{\rm{,}}\)\(c = 5\;{\rm{cm}}\), \(\widehat A = 120^\circ \). Các mệnh đề sau đúng hay sai?
a) \(S = \frac{1}{2}bc\cos A\).
b) \(a = \sqrt {127} \) cm.
c) \(\cos C \approx 0,91\).
d) \(R \approx 6,03\) cm.
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Cho các tập hợp khác rỗng \(A = \left[ {m - 1;\frac{{m + 3}}{2}} \right]\) và \(B = \left( { - \infty ; - 3} \right) \cup \left[ {3; + \infty } \right)\). Gọi \(S\) là tập hợp các giá nguyên dương của m để \(A \cap B \ne \emptyset \). Tìm số tập hợp con của \(S\).
Một hãng taxi có bảng giá như sau (sử dụng cho taxi 4 chỗ).

Bạn Trâm bắt taxi đi quãng đường 35 km thì phải trả số tiền là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng nghìn).
Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này với số vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800 000 đồng và lãi 150 000 đồng 1 áo, loại ngắn tay giá mua vào 600 000 đồng và lãi 120 000 đồng 1 áo. Cửa hàng ước tính nhu cầu của khách không quá 100 cái cho cả 2 loại. Để kinh doanh có lãi nhiều nhất thì cửa hàng cần nhập bao nhiêu áo dài tay.
Một viên bi được ném xiên từ vị trí A cách mặt đất 2 m theo quỹ đạo dạng parabol như hình vẽ sau đây. Tìm khoảng cách từ vị trí E đến vị trí F, biết rằng vị trí E là nơi viên bi rơi xuống chạm mặt đất (kết quả làm tròn đến hàng phần trăm).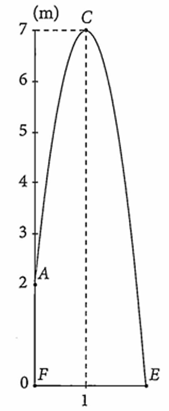
Cho góc α với \(\cot \alpha = 5\). Tính giá trị của biểu thức \(P = 2{\cos ^2}\alpha + 5\sin \alpha \cos \alpha + 1\) (kết quả làm tròn đến hàng phần trăm).
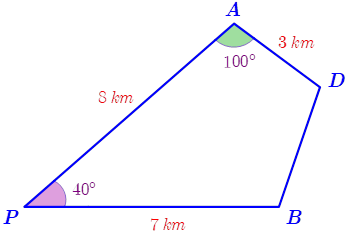
Hai bạn An và Hưng cùng xuất phát từ điểm \(P\), đi theo hai hướng khác nhau và tạo với nhau một góc \(40^\circ \) để đến đích là điểm \(D\). Biết rằng họ dừng lại để ăn trưa lần lượt tại \(A\) và \(B\) (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích (làm tròn kết quả đến hàng phần mười)?