Bộ 5 đề thi giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Đề 02
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phủ định của mệnh đề “\(1 + 2 = 3\)” là mệnh đề nào?
\(1 + 2 > 3\).
\(1 + 2 < 3\).
\(1 + 2 \ne 3\).
\(1 + 2 \le 3\).
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}\,} \right|\,\,4 \le x \le 9} \right\}\) được kết quả là
\(\left[ {4\,;9} \right]\).
\(\left( {4\,;9} \right]\).
\(\left[ {4\,;9} \right)\).
\(\left( {4\,;9} \right)\).
Cho \(A = \left[ { - 1;3} \right]\), \(B = \left( {2;5} \right)\). Tìm mệnh đề sai.
\(B\backslash A = \left( {3;5} \right)\).
\(A \cap B = \left( {2;3} \right]\).
\(A\backslash B = \left[ { - 1;2} \right]\).
\(A \cup B = \left[ { - 1;5} \right]\).
Trong các cặp số \(\left( {x\,;y} \right)\) sau đây, cặp nào là nghiệm của bất phương trình \[2x + y < 1\]?
\[\left( { - 2\,;1} \right)\].
\[\left( {0\,;1} \right)\].
\[\left( {3\,;7} \right)\].
\[\left( {2\,; - 1} \right)\].
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình\[\left\{ {\begin{array}{*{20}{c}}{x + 3y - 2 > 0}\\{2x - y + 1 < 0}\end{array}} \right.\]?
\[\left( {1;4} \right)\].
\[\left( { - 4;4} \right)\].
\[\left( {0;0} \right)\].
\[\left( { - 3;4} \right)\].
Miền không gạch chéo (không kể bờ \(d\)) trong hình sau là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây?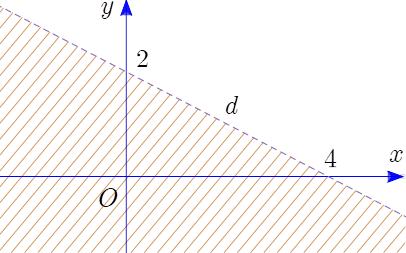
\[x + 2y < 4\].
\[2x + y \ge 4\].
\[x + 2y \ge 4\].
\[x + 2y > 4\].
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x - 1}},x \in \left( { - \infty ;2} \right]\\{x^2} - 1,x \in \left( {2;5} \right]\end{array} \right.\). Tính \(f\left( 3 \right)\).
\[8\].
\[7\].
\[2\].
Hàm số nào sau đây có đồ thị như hình dưới đây?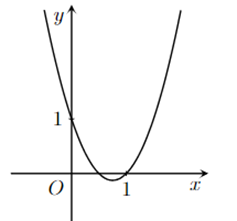
\[y = {x^2} - 3x + 1\].
\[y = - {x^2} + 3x - 1\].
\[y = - 2{x^2} + 3x - 1\].
\[y = 2{x^2} - 3x + 1\].
Cho parabol \(y = a{x^2} + bx + 4\) có trục đối xứng là đường thẳng \(x = \frac{1}{3}\) và đi qua điểm \(A\left( {1;3} \right)\). Tổng giá trị \(a + 2b\) là
\[ - \frac{1}{2}\].
\[\frac{1}{2}\].
\[ - 1\].
\[1\].
Trong các đẳng thức sau đây, đẳng thức nào đúng?
\(\sin 120^\circ = - \frac{{\sqrt 3 }}{2}\).
\(\cos 120^\circ = \frac{1}{2}\).
\(\tan 120^\circ = \sqrt 3 \).
\(\cot 120^\circ = - \frac{{\sqrt 3 }}{3}\).
Cho tam giác \(ABC\), có độ dài ba cạnh là \(BC = a,AC = b,AB = c\). Gọi \(R\) là bán kính đường tròn ngoại tiếp tam giác và \(S\) là diện tích tam giác đó. Mệnh đề nào sau đây sai?
\[{a^2} = {b^2} + {c^2} - 2bc\cos A\].
\[\frac{{\sin A}}{a} = \frac{{\sin B}}{b} = \frac{{\sin C}}{c}\].
\[S = \frac{{abc}}{R}\].
\[S = \sqrt {p(p - a)(p - b)(p - c)} \].
Tính diện tích tam giác có ba cạnh lần lượt là \(5\), \(12\) và \(13\).
\(S = 60\).
\(S = 30\).
\(S = 34\).
\(S = 7\sqrt 5 \).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các câu sau đúng hay sai?
a) Mệnh đề: “12 là số chính phương” là mệnh đề đúng.
b) \(A \cap B = \){\(x \in A\) và \(x \in B\)}.
c) Q: “Tam giác ABC là tam giác cân” có mệnh đề phủ định là \(\overline Q \): “Tam giác ABC không là tam giác vuông”.
d) Lớp 10A có 18 học sinh tham gia câu lạc bộ bóng đá và 15 học sinh tham gia câu lạc bộ bóng rổ. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên. Khi đó có 23 học sinh tham gia ít nhất một trong hai câu lạc bộ trên.
Cho hệ bất phương trình \(\left\{ \begin{array}{l} - 2x + y \le 2\\ - x + 2y \ge 4\\x + y \ge 5\end{array} \right.\) . Các mệnh đề sau là đúng hay sai?
a) Hệ trên không phải là một hệ bất phương trình bậc nhất hai ẩn.
b) (−1; 2) là một nghiệm của hệ bất phương trình trên.
c) Miền nghiệm của hệ bất phương trên là miền tam giác ABC có tọa độ các đỉnh \(A\left( {2;0} \right),C\left( {2;3} \right),B\left( {1;4} \right)\) bao gồm cả các cạnh.
d) Giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = x - 2y\) là 2.
Cho hàm số bậc hai \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ sau
Các mệnh đề sau đúng hay sai?
a) \(a > 0\).
b) \(c > 0\).
c) \(a - 2b + c = 7\).
d) \(a - {b^2} + {c^3} = 10\).
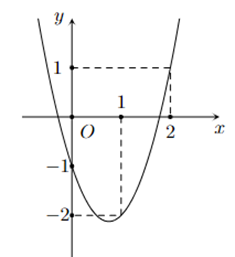
Cho tam giác \(ABC\) biết cạnh \(a = 137,5\;{\rm{cm}}\), \(\widehat B = 83^\circ \), \(\widehat C = 57^\circ \). Các mệnh đề sau đúng hay sai?
a) \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\).
b) \(\widehat A = 40^\circ \).
c) \(R \approx 106,96\) cm.
d) \(b \approx 179,4\)cm.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa (biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong ba môn Toán, Lý, Hóa).
Bạn Lan mang 150 000 đồng đi nhà sách để mua một số quyển tập và bút. Biết rằng giá một quyển tập là 8 000 đồng và giá của một cây bút là 6 000 đồng. Bạn Lan có thể mua được tối đa bao nhiêu quyển tập nếu bạn đã mua 10 cây bút.
Một công ty trong một đợt quảng cáo và bán khuyến mãi hàng hóa cần thuê xe để chở trên \(140\) người và trên \(9\) tấn hàng. Nơi thuê chỉ có hai loại xe \(A\) và \(B\). Trong đó xe loại \(A\) có \(10\) chiếc, xe loại \(B\) có \(9\) chiếc. Một chiếc xe loại \(A\) cho thuê với giá \(4\) triệu, loại \(B\) giá \(3\) triệu. Biết rằng xe \(A\) chỉ chở tối đa \(20\) người và \(0,6\)tấn hàng. Xe \(B\) chở tối đa \(10\) người và \(1,5\) tấn hàng. Hỏi chi phí vận chuyển là thấp nhất mà công ty phải trả là bao nhiêu triệu?
Một quả bóng được đá lên từ độ cao 1,5 mét so với mặt đất. Biết quỹ đạo của quả bóng là một đường parabol trong mặt phẳng tọa độ \(Oxy\) có phương trình là \(h = a{t^2} + bt + c\left( {a < 0} \right)\) trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và h là độ cao (tính bằng mét) của quả bóng. Biết rằng sau 2 giây thì nó đạt độ cao 5 m; sau 4 giây nó đạt độ cao 4,5 m. Hỏi sau 5,5 giây quả bóng đạt độ cao bao nhiêu mét so với mặt đất?
Giá trị của biểu thức \(B = \frac{{2{{\sin }^2}30^\circ }}{{1 - 2{{\cos }^2}30}} + 4\sin 60^\circ - \cot 30^\circ \) có dạng \(a + b\sqrt 3 \) trong đó \(a,b \in \mathbb{Z}\). Tính \(a + b\).
Từ vị trí người ta quan sát một cây cao.
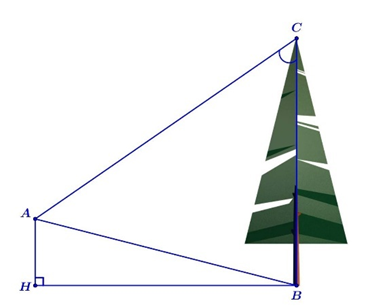
Biết \(AH = 4\;{\rm{m}}\), \(HB = 20\;{\rm{m}}\), \(\widehat {BAC} = 45^\circ \). Tính chiều cao của cây (làm tròn kết quả đến hàng phần mười).








