Bộ 5 đề thi giữa kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Đề 01
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu nào là một mệnh đề?
13 là số nguyên tố.
Bây giờ là mấy giờ?
Cảnh báo đường trơn, lái xe cẩn thận!
Các em phải học hành chăm chỉ nhé!
Khẳng định nào sau đây là đúng?
\(\mathbb{R} \subset \mathbb{Q}\).
\(\mathbb{Z} \subset \mathbb{N}\).
\(\mathbb{Q} \subset \mathbb{Z}\).
\(\mathbb{N} \subset \mathbb{R}\).
Cho hai tập hợp \(X = \left\{ {2;4;8;10;12} \right\}\) và \(Y = \left\{ {3;4;5;6;7;8;9} \right\}\). Khi đó tập hợp \(X\backslash Y\) có bao nhiêu phần tử?
3.
4.
5.
6.
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(3x + 2y \ge 0.\)
\({x^2} + {y^2} < 2.\)
\(2{x^2} + 3y > 0.\)
\(x + {y^2} \ge 0.\)
Điểm \(O\left( {0;0} \right)\) không thuộc miền nghiệm của hệ bất phương trình nào sau đây?
\(\left\{ \begin{array}{l}x + 3y < 0\\2x + y + 4 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 3y \ge 0\\2x + y - 4 < 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 3y - 6 < 0\\2x + y + 4 > 0\end{array} \right.\) .
\(\left\{ \begin{array}{l}x + 3y - 6 < 0\\2x + y + 4 \ge 0\end{array} \right.\).
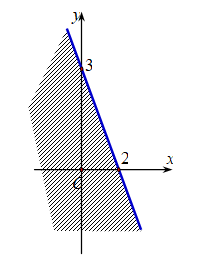
Miền nghiệm của bất phương trình \(3x + 2y \ge 6\) là
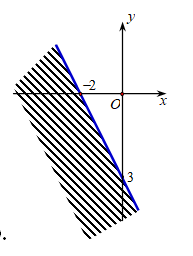
Tìm tập xác định của hàm số \(y = \frac{{x - 2}}{{x - 1}}\).
\(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {1;2} \right\}.\)
\(D = \mathbb{R}.\)
\(D = \mathbb{R}\backslash \left\{ 2 \right\}.\)
Trong các hàm số sau hàm số nào là hàm số bậc hai?
\(y = 2{x^2} + 3x - 5.\)
\(y = \frac{{2{x^3} + 3x - 5}}{x}.\)
\(y = 2{x^2} + 3{x^3} - 5.\)
\(y = 3x + 2.\)
Cho hàm số bậc hai \(y = f\left( x \right)\) có đồ thị như hình vẽ. Tập nghiệm của bất phương trình \(f\left( x \right) > 0\) là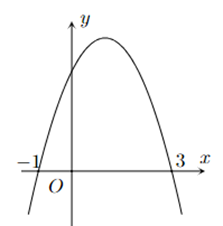
\(\left( {0;3} \right).\)
\(\left[ { - 1;3} \right].\)
\(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right).\)
\(\left( { - 1;3} \right).\)
Cho góc α tù. Khẳng định nào sau đây là đúng?
\(\cos \alpha < 0\).
\(\cot \alpha > 0\).
\(\sin \alpha < 0\).
\(\tan \alpha > 0\).
Cho \(\Delta ABC\) có \(a = 4,c = 5,\widehat B = 150^\circ \). Tính diện tích tam giác \(ABC\).
\(S = 10\).
\(S = 10\sqrt 3 \).
\(S = 5\).
\(S = 5\sqrt 3 \).
Cho \(\Delta ABC\) có \(AB = 4;AC = 6;\widehat A = 120^\circ \). Độ dài cạnh BC là
\(\sqrt {19} \).
\(3\sqrt {19} \).
\(2\sqrt {19} \).
\(2\sqrt 7 \).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các câu sau đúng hay sai?
a) Cho hai mệnh đề P: “Tứ giác ABCD là hình vuông” và mệnh đề Q: “Tứ giác ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau”. Mệnh đề đảo của mệnh đề P Þ Q là mệnh đề: “Nếu ABCD là hình chữ nhật có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình vuông”.
b) \(A \cup B = \){\(x|x \in A\) và \(x \in B\)}.
c) Mệnh đề phủ định của mệnh đề \(\forall x \in \mathbb{R},{x^2} + 1 = 0\) là \(\exists x \in \mathbb{R},{x^2} + 1 \ne 0\).
d) Lớp 10A có tất cả 40 học sinh trong đó có 13 học sinh chỉ thích đá bóng, 18 học sinh chỉ thích chơi cầu lông và số học sinh còn lại thích chơi cả hai môn thể thao nói trên. Vậy, có 27 học sinh thích chơi cả hai môn cầu lông và đá bóng.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}3x + 2y \ge 9\\x - 2y \le 3\\x + y \le 6\\x \ge 1\end{array} \right.\) (I). Khi đó:
a) Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) (3; 2) là một nghiệm của hệ bất phương trình.
c) Miền nghiệm của hệ bất phương trình là miền tam giác.
d) \(x = 1;y = 3\) là nghiệm của hệ bất phương trình (I) sao cho \(F = 3x - y\) đạt giá trị lớn nhất.
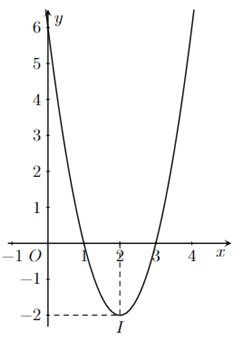
Cho đồ thị hàm số bậc hai \(y = f\left( x \right)\) có dạng như hình bên:
Các câu sau đúng hay sai?
a) Trục đối xứng của đồ thị là đường thẳng \(x = - 2\).
b) Đỉnh I của đồ thị hàm số có tọa độ là \(\left( {2; - 2} \right)\).
c) Đường thẳng \(y = m + 2\) cắt đồ thị hàm số tại hai điểm phân biệt khi và chỉ khi \(m > - 1\).
d) Hàm số đã cho là \(y = 2{x^2} - 2x + 6\).
Cho có \(BC = \sqrt 6 ,CA = 2,AB = 1 + \sqrt 3 \). Các mệnh đề sau đúng hay sai?
a) \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos \widehat {\rm{A}}\).
b) \(\widehat B = 35^\circ \).
c) \(S = \frac{{3 + \sqrt 3 }}{2}\).
d) \(R = \sqrt 2 \).
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10A đưa ra ba nhóm ngành cho học sinh lựa chọn đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có 6 học sinh chọn nhóm ngành Giáo dục, 9 học sinh chọn nhóm ngành Y tế, 10 học sinh chọn nhóm ngành Công nghệ thông tin, 22 học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có 3 học sinh chọn hai nhóm ngành Giáo dục và Y tế, 2 học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, 3 học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Hỏi có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10A có 40 học sinh.
Bạn Nam tiết kiệm được 450 nghìn đồng. Trong đợt ủng hộ các bạn học sinh đồng bào miền Trung bị lũ lụt vừa qua, bạn Nam đã ủng hộ \(x\) tờ tiền loại 20 nghìn đồng, \(y\)tờ tiền loại 10 nghìn đồng. Khi đó bất phương trình biểu diễn tổng số tiền mà bạn Nam đã ủng hộ có dạng \(ax + by \le c\). Tính giá trị của biểu thức \(P = c - 2a - b\).
Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi thu được khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900. Gọi \({x_0};{y_0}\) lần lượt là số radio kiểu một và radio kiểu hai sản xuất được trong một ngày để tiền lãi thu được là nhiều nhất. Tính tổng \(T = {x_0} + 2{y_0}\).
Một cửa hàng kinh doanh giày và giá để nhập một đôi giày là 40 đô la. Theo nghiên cứu của bộ phận kinh doanh thì nếu cửa hàng bán mỗi đôi giày với giá \(x\) đô la thì mỗi tháng sẽ bán được \(120 - x\) đôi giày. Hỏi cửa hàng bán giá bao nhiêu cho một đôi giày để có thể thu lãi cao nhất trong tháng?
Cho \(\tan \alpha = - 1\). Tính giá trị của biểu thức \(P = \frac{{\sin \alpha + 2\cos \alpha }}{{\cos \alpha + 2\sin \alpha }}\).
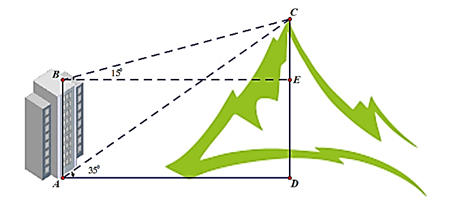
Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang \[35^\circ \] và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang \[15^\circ \] (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao \[60\left( {\rm{m}} \right)\] (làm tròn đến hàng phần trăm).