Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 4
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) là
\(x \ne 0;\,\,x \ne 1.\)
\(x \ne 0;\,\,x \ne - 1.\)
\(x \ne 3;\,\,x \ne 2.\)
\(x \ne 0.\)
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\(5x - y = 3.\)
\(\sqrt 3 x + 0y = 3.\)
\(0x + 2y = \sqrt 7 .\)
\(0x + 0y = 4.\)
Trong các hệ phương trình sau, đâu không phải là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}3x - y = 5\\x + 2y = - 1\end{array} \right..\)
\(\left\{ \begin{array}{l} - 3y = 6\\3x + 5y = 15\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} - 4{y^2} = 0\\2x + 5y = 7\end{array} \right..\)
\(\left\{ \begin{array}{l}2x - 3y = - 3\\2x + 5y = 7\end{array} \right..\)
Phát biểu “\(x\) không lớn hơn \( - 100\)” được viết là
\(x > - 100.\)
\(x \ge - 100.\)
\(x < - 100.\)
\(x \le - 100.\)
Biết rằng \(m > n\) với \(m,\,n\) bất kì. Khẳng định nào dưới đây là đúng?
\(m - 3 > n - 3.\)
\(m + 3 < n + 3.\)
\(m - 2 < n - 2.\)
\(n + 2 > m + 2.\)
Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?
\({\left( { - \sqrt 5 } \right)^2}.\)
\(\sqrt {{5^2}} .\)
\(\sqrt {{{\left( { - 5} \right)}^2}} .\)
\( - {\left( {\sqrt 5 } \right)^2}.\)
Điều kiện xác định của biểu thức \(A = \sqrt {1 - 2x} \) là
\(x \le \frac{1}{2}.\)
\(x < \frac{1}{2}.\)
\(x > \frac{1}{2}.\)
\(x \ge \frac{1}{2}.\)
Thu gọn biểu thức \(\sqrt[3]{{{{\left( {5 - x} \right)}^3}}}\) được
\({\left( {5 - x} \right)^3}.\)
\(5 - x.\)
\(x - 5.\)
\(\left| {5 - x} \right|.\)
Với mọi góc nhọn \(\alpha \), ta có
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\tan \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = 1 - \tan \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = \sin \alpha .\)
Cho \(\Delta MNP\) vuông tại \(N\). Hệ thức nào sau đây là đúng?
\(NP = MN \cdot \tan P.\)
\(NP = MN \cdot \cos P.\)
\(NP = MP \cdot \cos P.\)
\(NP = MP \cdot \cot P.\)
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn
Cắt nhau.
Tiếp xúc nhau.
Ngoài nhau.
Không xác định.
Đường thẳng \(d\) cách tâm \(O\) của đường tròn \(\left( {O;\,\,4\,{\rm{cm}}} \right)\) một khoảng \({\rm{3 cm}}.\) Khi đó vị trí tương đối của \(d\) và đường tròn \(\left( {O;\,\,4\,{\rm{cm}}} \right)\) là
cắt nhau.
không giao nhau.
tiếp xúc nhau.
không kết luận được.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Bạn An mua một quyển sách bồi dưỡng Toán và một quyển sách bồi dưỡng Ngữ Văn với tổng số tiền theo giá niêm yết là \(270{\rm{ }}000\) đồng. Vì An mua vào lúc cửa hàng có chương trình giảm giá nên khi thanh toán quyển sách Toán được giảm giá \(10\% \); quyển sách Ngữ Văn được giảm giá \(20\% .\) Do đó An chỉ cần phải trả \(228{\rm{ }}000\) đồng. Gọi giá niêm yết của quyển sách bồi dưỡng Toán và quyển sách bồi dưỡng Ngữ Văn lần lượt là \(x,{\rm{ }}y\) (đồng).
a) Điều kiện xác định \(x > 0,{\rm{ }}y > 0.\)
b)\(x + y = 270{\rm{ }}000\).
c)\(\left\{ \begin{array}{l}x + y = 270{\rm{ }}000\\0,9x + 0,8y = 228{\rm{ }}000\end{array} \right.\).
d) Giá niêm yết của quyển sách bồi dưỡng Toán là \(150{\rm{ }}000\) đồng và quyển sách bồi dưỡng Ngữ Văn là \(120{\rm{ }}000\) đồng.
Một người quan sát một tòa nhà và đứng cách tòa nhà khoảng \[25{\rm{\;m}}\]. Góc nâng từ mắt người quan sát đến nóc tòa nhà là \[36^\circ \]. Nếu anh ta đi thêm \[5{\rm{\;m}}\] nữa, đến vị trí \[E\] nằm giữa \[C\] và \[H\], thì có góc nâng mới từ \[F\] đến nóc tòa nhà. Chiều cao \[CD\] tính từ chân đến mắt người quan sát là \[1,6{\rm{\;m}}{\rm{.}}\] (Các kết quả làm tròn đến hàng đơn vị)
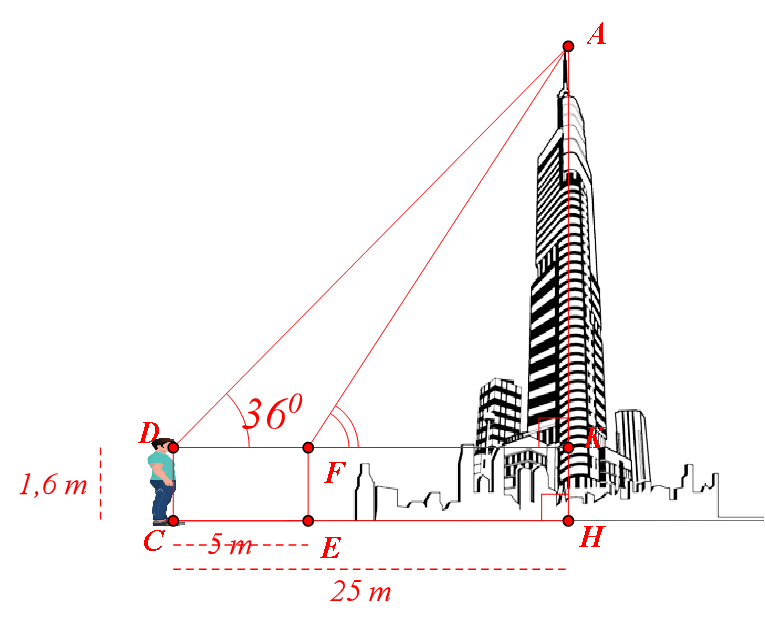
a) \[AK = KD \cdot \tan 36^\circ .\]
b) \[FK = 25{\rm{\;m}}{\rm{.}}\]
c) Độ dài tòa nhà lớn hơn 20 m.
d) Góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}} = \frac{{12}}{{1 - 9{x^2}}}.\)
Tìm giá trị nguyên nhỏ nhất của \(x\) thỏa mãn bất phương trình: \(3x - \left( {6 + 2x} \right) \le 5\left( {x + 4} \right)\).
Tính giá trị của biểu thức \(A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) khi \(x = 25.\)
Cho đường tròn \(\left( {O;{\rm{ }}12{\rm{ cm}}} \right)\), dây \(AB\) vuông góc với bán kính \(OC\) tại trung điểm \(M\) của \(OC\). Dây \(AB\) có độ dài bao nhiêu centimet? (Kết quả làm tròn đến hàng phần mười)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \[T = \left( {\frac{{a\sqrt a - 1}}{{a - \sqrt a }} - \frac{{a\sqrt a + 1}}{{a + \sqrt a }}} \right):\frac{{a + 1}}{{a - 1}}\] với \[a > 0,{\rm{ }}a \ne 1\].
a) Chứng minh rằng \[T = \frac{{2\left( {a - 1} \right)}}{{a + 1}}\].
b) Tìm các giá trị nguyên của \[a\] để \[T\] nhận giá trị nguyên.
(1,5 điểm) Cho đường tròn \(\left( O \right)\) và một điểm \(A\) nằm ngoài đường tròn. Các tiếp tuyến với đường tròn kẻ từ \(A\) tiếp xúc với đường tròn tại \(B\) và \(C\). Gọi \(H\) là giao điểm của \(OA\) và \(BC\), kẻ đường kính \(BD\) của đường tròn \(\left( O \right)\), hạ \(CM \bot BD\) tại \(M.\) Tia \(AO\) cắt đường tròn \(\left( O \right)\) tại \(E,F\).
a) Chứng minh rằng .
b) Chứng minh rằng \[BE\] là phân giác của \(\widehat {ABC}.\)
c) Cho \[\widehat {DCM} = 30^\circ \] và \[AH = 4{\rm{ cm}}\]. Tính diện tích hình quạt giới hạn bởi các bán kính \[OB,OC\] và cung nhỏ \(BC\).
(0,5 điểm)Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\)và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.








