Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 3
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phương trình \(\frac{x}{{2x + 1}} + \frac{3}{{x - 5}} = \frac{x}{{\left( {2x + 1} \right)\left( {x - 5} \right)}}\) là
\(x \ne - \frac{1}{2}.\)
\(x \ne - \frac{1}{2}\)và \(x \ne 5.\)
\(x \ne - 5.\)
\(x \ne \frac{1}{2}\) và \(x \ne - 5.\)
Trong các hệ thức sau, hệ thức nào không phải là phương trình bậc nhất hai ẩn?
\(0x - 0y = 8.\)
\(0x - 2y = 0.\)
\(3x + 0y = 1.\)
\( - 3x + 3y = 3.\)
Trong các hệ phương trình sau, hệ phương trình bậc nhất hai ẩn \(x\) và \(y\) là
\(\left\{ \begin{array}{l}3x - y = 2\\x + 2y = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}0x - 0y = 5\\2x + y = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}x - y = 2\\x + {y^2} = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}2{x^2} - y = 2\\x + y = - 1\end{array} \right..\)
Bất đẳng thức diễn tả khẳng định “\(n\) không nhỏ hơn \(\frac{9}{4}\)” là
\(n \le \frac{9}{4}.\)
\(n < \frac{9}{4}.\)
\(n > \frac{9}{4}.\)
\(n \ge \frac{9}{4}.\)
Cho \(m\) bất kỳ. Kết quả so sánh nào sau đây là đúng?
\(m - 3 > m - 4.\)
\(m - 3 < m - 5.\)
\(m - 3 \ge m - 2.\)
\(m - 3 \le m - 6.\)
Điều kiện xác định của \(\sqrt {16 - x} \) là
\(x < 16.\)
\(x > 16.\)
\(x \ge 16.\)
\(x \le 16.\)
Biểu thức nào sau đây là căn thức bậc ba?
\(\sqrt {{x^3}} .\)
\({\left( {\sqrt x - 1} \right)^3}.\)
\(\sqrt[3]{{x + 1}}.\)
\(\sqrt {{{\left( {2x + 1} \right)}^3}} .\)
Nếu \(\sqrt {{a^2}} = - a\) thì
\(a \ge 0.\)
\(a = - 1.\)
\(a \le 0.\)
\(a = 0.\)
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó:
\(AC = AB.\cot C.\)
\(AC = AB.\cot B.\)
\(AC = BC.\cot C.\)
\(AC = BC.\cot B.\)
Cho tam giác \(A\) có đường cao \(AH\) như hình vẽ.
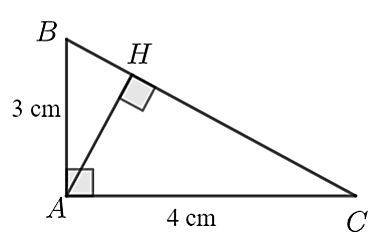
Khẳng định nào đúng?
\(\cot \widehat {CAH} = \frac{3}{4}.\)
\(\cot \widehat {CAH} = \frac{3}{5}.\)
\(\cot \widehat {CAH} = \frac{4}{3}.\)
\(\cot \widehat {CAH} = \frac{4}{5}.\)
Trong hình bên \(\widehat {ACB}\) là góc gì?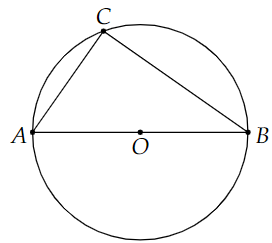
Góc vuông.
Góc tù.
Góc nhọn.
Góc bẹt.
Cho đường tròn \(\left( {O;\,\,{\rm{6 cm}}} \right)\) và đường tròn \(\left( {O';\,\,{\rm{4 cm}}} \right)\). Biết hai đường tròn này cắt nhau nên
\(OO' > 10{\rm{ cm}}{\rm{.}}\)
\(OO' = 10{\rm{ cm}}{\rm{.}}\)
\(OO' < 10{\rm{ cm}}{\rm{.}}\)
\(2{\rm{ cm}} < OO' < 10{\rm{ cm}}{\rm{.}}\)
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Hai tổ cùng làm một công việc trong \(15\) giờ thì xong. Nếu tổ I làm trong \(3\) giờ, tổ II làm trong \(5\) giờ thì được \(25\% \) công việc. Gọi \(x,\,\,y\) (giờ) lần lượt là số giờ tổ I, tổ II làm riêng để hoàn thành toàn bộ công việc \(\left( {x,\,\,y > 0} \right).\)
a) Trong 1 giờ, tổ I làm được \(\frac{1}{x}\) (công việc); tổ II làm được \(\frac{1}{y}\) (công việc).
b) Trong 3 giờ, tổ I làm được \(\frac{3}{x}\) (công việc); trong 5 giờ tổ II làm được \(\frac{5}{y}\) (công việc).
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = 15\\\frac{3}{x} + \frac{5}{y} = \frac{1}{4}\end{array} \right.\).
d) Nếu làm riêng thì tổ I hoàn thành công việc trong 40 giờ, tổ II hoàn thành trong 24 giờ.
Sau một trận bão lớn, một cái cây mọc thẳng đứng ở vị trí \(C\) đã bị gãy ngang tại \(A\) (như hình vẽ). Ngọn cây chạm mặt đất cách gốc một khoảng \(BC = 5{\rm{ m}}\). Biết rằng phần ngọn bị gãy \(AB\) và phần gốc \(AC\) có tỉ lệ \(3:2\). (Các kết quả làm tròn đến chữ số thập phân thứ hai)
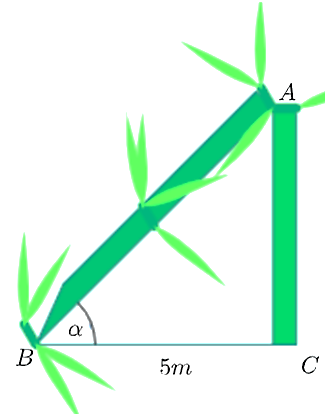
a)\(\sin \widehat {ABC} = \frac{2}{3}.\)
b) Góc tạo bởi phần thân bị gãy và mặt đất nhỏ hơn \(42^\circ \).
c) Độ dài phần ngọn bị gãy nhỏ hơn \(6,5{\rm{ m}}{\rm{.}}\)
d) Chiều cao ban đầu của cây khoảng \(11,18{\rm{ m}}{\rm{.}}\)
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình \(\frac{{2x - 5}}{{x - 3}} - \frac{1}{x} = \frac{{6x + 3}}{{{x^2} - 3x}}\)?
Hỏi giá trị nguyên lớn nhất của \(x\) thỏa mãn bất phương trình \[\frac{{x + 1}}{3} - \frac{{x - 2}}{2} \ge 4\] là bao nhiêu?
Tính giá trị của biểu thức \(B = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}\) khi \(x = \frac{1}{{16}}.\) (Kết quả ghi dưới dạng số thập phân)
Cung tròn \(50^\circ \) của một đường tròn có độ dài là \(\pi {\rm{\;cm}}.\) Tính bán kính của đường tròn đó.
(Kết quả ghi dưới dạng số thập phân)
TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cho hai biểu thức: \[A = \left( {\frac{{\sqrt a }}{2} - \frac{1}{{2\sqrt a }}} \right)\left( {\frac{{a - \sqrt a }}{{\sqrt a + 1}} - \frac{{a + \sqrt a }}{{\sqrt a - 1}}} \right)\] với \(a > 0,{\rm{ }}a \ne 1\).
a) Rút gọn biểu thức \(A.\)
b) Tính giá trị của \(A\) khi \(\left| {a - 1} \right| = 1\).
(1,5 điểm) Cho đường tròn \[\left( O \right)\] và điểm \[A\] nằm bên ngoài đường tròn. Từ \[A\] kẻ hai tiếp tuyến \[AM,AN\] với đường tròn \[\left( O \right)\]. Một đường thẳng \[d\] đi qua \[A\] cắt đường tròn \[\left( O \right)\] tại hai điểm \[B\] và \[C\] (\[AB < AC\], \[d\] không đi qua tâm \[O\]). Gọi \[I\] là trung điểm của \[BC\]. Đường thẳng \[NI\] cắt đường tròn \[\left( O \right)\] tại điểm thứ hai là \[F\].
a) Chứng minh bốn điểm \[A,M,O,N\] cùng thuộc một đường tròn.
b) Chứng minh \[MF\,{\rm{//}}\,AC\].
c) Hai tiếp tuyến của đường tròn \[\left( O \right)\] tại \[B\] và \[C\] cắt nhau tại \[K\]. Chứng minh \[K\] thuộc một đường tròn cố định khi \[d\] thay đổi.
(0,5 điểm)Một sợi dây thép \(AC\) có chiều dài \({\rm{8 m}}\)được chia thành hai phần \(AB,\,\,BC\) (như hình vẽ minh họa dưới đây).
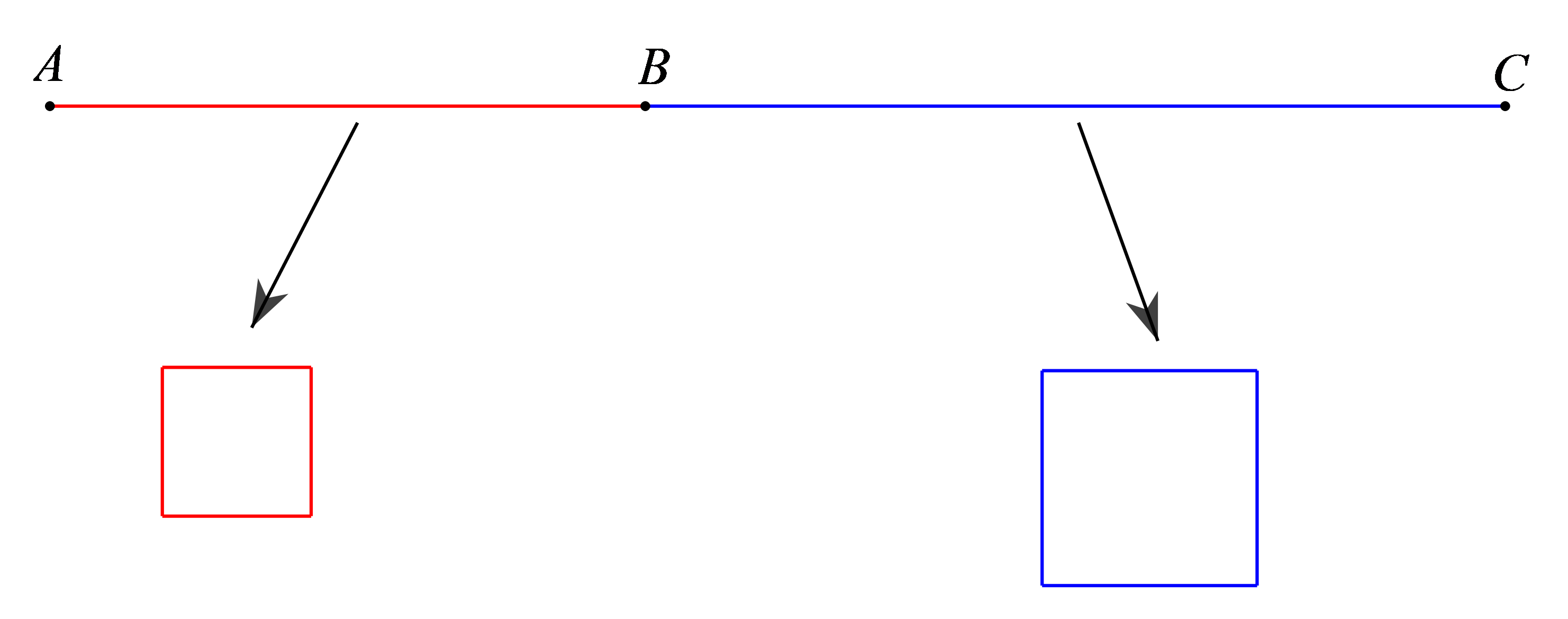
Mỗi phần đều được uốn thành một hình vuông. Hỏi phải chia sợi dây ban đầu như thế nào để tổng diện tích hai hình vuông thu được sau khi uốn là nhỏ nhất?








