Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 1
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x - 4}} + 1 = \frac{3}{{x + 2}}\) là
\(x \ne - 4;\,\,x \ne 2.\)
\(x \ne 4;\,\,x \ne - 2.\)
\(x \ne 4;\,\,x \ne 2.\)
\(x \ne 4;\,\,x \ne 2.\)
Trong các hệ thức sau, hệ thức nào không phải là phương trình bậc nhất hai ẩn?
\(x - 2y = 3.\)
\(0x + 3y = 1.\)
\(0x - 0y = 5.\)
\(2x - 0y = 4.\)
Trong các hệ phương trình dưới đây, đâu là phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x - y = 3\\{x^2} + y = 4\end{array} \right..\)
\(\left\{ \begin{array}{l}3x - y = 5\\0x + 0y = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}2x + y = 4\\x + {y^2} = 3\end{array} \right..\)
\(\left\{ \begin{array}{l}4x + y = 5\\x - 3y = 2\end{array} \right..\)
Cho \(a\) bất kì. Kết quả so sánh nào dưới đây là đúng?
\(a - 4 > a - 5.\)
\(a - 3 < a - 4.\)
\(a - 2 \le a - 4.\)
\(a - 7 \ge a - 9.\)
Phát biểu “\(x\) không lớn hơn \( - \frac{{10}}{3}\)” được viết là
\(x > - \frac{{10}}{3}.\)
\(x \ge - \frac{{10}}{3}.\)
\(x < - \frac{{10}}{3}.\)
\(x \le - \frac{{10}}{3}.\)
Điều kiện xác định của căn thức \(\sqrt {\frac{2}{{x - 1}}} \) là
\(x \ge 1.\)
\(x > 1.\)
\(x < 1.\)
\(x \le 1.\)\(x - 1 > 0\)\(x > 1.\)
Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}} \) bằng
\(3 - 2x.\)
\(2x - 3.\)
\(\left| {2x - 3} \right|.\)
\(2x - 3\) và \( - 2x + 3\).
Rút gọn \[\sqrt[3]{{{{\left( {1 - x} \right)}^3}}}\] ta được
\(\left| {1 - x} \right|.\)
\(1 - x.\)
\(x - 1.\)
Cả A, B, C đều sai.
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3;\,\,AB = 4;\,\,BC = 5.\) Khi đó \(\tan C\) bằng
\(\frac{3}{4}.\)
\(\frac{3}{5}.\)
\(\frac{4}{3}.\)
\(\frac{4}{5}.\)
Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào dưới đây là sai?
\(\sin B = \cos C.\)
\(\cos B = \sin C.\)
\(\cot B = \tan C.\)
\(\tan B = \frac{1}{{\cot C}}.\)
Góc ở tâm chắn cung \(160^\circ \) có số đo bằng bao nhiêu?
\(200^\circ .\)
\(160^\circ \).
\(80^\circ \).
\(20^\circ .\)
Cho đường tròn \(\left( {O;{\rm{ 4 cm}}} \right)\) và \(\left( {O';{\rm{ 3 cm}}} \right)\) có \(OO' = 5{\rm{ cm}}{\rm{.}}\) Vị trí tương đối của hai đường tròn đã cho là
tiếp xúc trong.
cắt nhau.
tiếp xúc ngoài.
đựng nhau.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Lan có một dung dịch nước muối sinh lí có nồng độ \(1,5\% \) và một dung dịch nước cất không chứa muối (nồng độ \(0\% \)). Lan cần pha trộn dung dịch để thu được 1 lít (1000 ml) dung dịch nước muối dinh lí súc miệng có nồng độ 0,9%. Gọi (ml) là thể tích dung dịch nước muối và \(y\) (ml) là thể tích nước cất \(0\% \) (\(x,{\rm{ }}y > 0\)).
a) Phương trình biểu diễn tổng thể tích dung dịch là \(x + y = 1\,\,000\).
b) Phương trình biểu diễn lượng muối trong dung dịch ban đầu là .
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}x + y = 1\,\,000\\0,015x + y = 900\end{array} \right.\).
d) Lan cần pha \(600{\rm{ ml}}\) dung dịch nước muối \(1,5\% \) và \(400{\rm{ ml}}\) dung dịch nước cốt \(0\% \) để được dung dịch mong muốn.\(1,5\% .x\)
Trên nóc của một tòa nhà có một cột ăng – ten cao \(5{\rm{ m}}\). Từ vị trí quan sát \(A\) cao \(7{\rm{ m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và đỉnh \(C\) của một cột ăng – ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang.
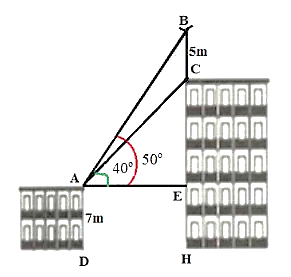
a) \(CE = AE.\tan 40^\circ .\)
b) \(BE = AE.\tan 50^\circ .\)
c) \(AE = \frac{{BC}}{{\tan 40^\circ + \tan 50^\circ }}\).
d) Chiều cao của tòa nhà lớn hơn 24 m.
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình \(\frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}} = \frac{4}{{1 - 9{x^2}}}\)?
Tìm giá trị nguyên nhỏ nhất của \[x\] thỏa mãn bất phương trình \[\frac{{4x + 9}}{3} + \frac{1}{2} \ge \frac{{2x - 1}}{4}\].
Tính giá trị của biểu thức \[A = \frac{{\sqrt x - 2}}{{\sqrt x + 7}}\] tại \[x = 25.\] (Kết quả ghi dưới dạng số thập phân)
Mặt đĩa CD có dạng vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là \[4{\rm{ cm}}\] và \[6{\rm{ cm}}\]. Hình vành khuyên đó có diện tích bằng bao nhiêu centimet vuông? (Kết quả làm tròn đến hàng phần mười)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cho biểu thức \(P = \left( {\frac{{x - 2}}{{x + 2\sqrt x }} + \frac{1}{{\sqrt x + 2}}} \right) \cdot \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\) với \(x > 0\) và
a) Chứng minh rằng \(P = \frac{{\sqrt x + 1}}{{\sqrt x }}.\)
b) Tìm các giá trị của \(x\) để \(2P = 2\sqrt x + 5\).
(1,5 điểm) Trên đường thẳng \(xy\), lấy lần lượt ba điểm \(A,B,C\) sao cho \(AB > BC\). Vẽ đường tròn \(\left( O \right)\) đường kính \(AB\) và đường tròn \(\left( {O'} \right)\) đường kính .
a) Gọi \(H\) là trung điểm của \(AC\). Vẽ dây \(DE\) của đường tròn \(\left( O \right)\) vuông góc với \(AC\) tại \(H\). Chứng minh tứ giác \(ADCE\) là hình thoi.
b)\(DC\) cắt đường tròn \(\left( {O'} \right)\) tại \(F\). Chứng minh rằng ba điểm \(F,B,E\) thẳng hàng.
c) Chứng minh rằng \(HF\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\).
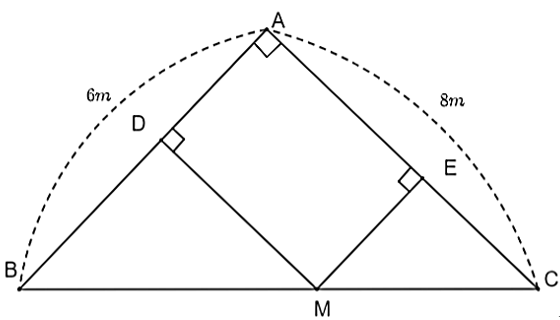
(0,5 điểm) Một người đào ao cá trên thửa ruộng dạng hình tam giác vuông \[ABC\] tại \[A\] có độ dài các cạnh góc vuông \[AB = 6{\rm{ m,}}\]\[AC = 8{\rm{ m}}{\rm{.}}\] Một chiếc máy xúc ở vị trí điểm \[M\] di chuyển trên bờ \[BC.\] Gọi \[MD\] và \[ME\] là khoảng cách từ \[M\] đến bờ \[AB,AC.\]Người đó đào được ao là tứ giác \[ADME\]. Tính diện tích lớn nhất của ao cá mà người đó có thể đào.