Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 8
16 câu hỏi
Mẫu thức chung đơn giản nhất khi quy đồng mẫu thức hai vế của phương trình \(\frac{{x + 3}}{{x - 3}} + \frac{{2x - 1}}{{3 - x}} = 5\) là
\(x - 3\).
\(\left( {x - 3} \right)\left( {3 - x} \right)\).
\({\left( {x - 3} \right)^2}\).
\(5\left( {x - 3} \right)\).
Tổng các nghiệm của phương trình \(\left( {\frac{1}{3}x - 3} \right)\left( {x + 8} \right) = 0\) là
\(5\).
\(1\).
\( - 5\).
\( - 1\).
Sau khi thực hiện các bước giải hệ phương trình \(\left\{ \begin{array}{l}2x + y = 1\\ - 4x - 2y = - 2\end{array} \right.\) theo phương pháp cộng đại số, bạn An được phương trình \(0x = 0.\) Bạn An cần viết kết luận về nghiệm của hệ phương trình như nào?
Vậy hệ phương trình vô nghiệm.
Vậy hệ phương trình có nghiệm duy nhất là \(\left( {0;\,\,1} \right)\).
Vậy hệ phương trình có vô số nghiệm. Nghiệm tổng quát của hệ được viết là \(\left( {x;\,\,2x - 1} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Vậy hệ phương trình có vô số nghiệm. Nghiệm tổng quát của hệ được viết là \(\left( {x;\,\,1 - 2x} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Cho hệ phương trình \(\left\{ \begin{array}{l}x - y = 8\\2x + 3y = - 9\end{array} \right..\) Cho các khẳng định sau:
(i) Từ phương trình thứ nhất của hệ, biểu diễn \(y\) theo \(x,\) ta được: \(y = x - 8\).
(ii) Từ phương trình thứ nhất của hệ, biểu diễn \(x\) theo \(y,\) ta được: \(x = 8 - y.\)
(iii) Nghiệm của hệ là cặp số \(\left( {3;\,\, - 5} \right)\).
Số khẳng định đúng trong các khẳng định trên là
0.
1.
2.
3.
Cho số thực \(a\). Khẳng định nào sau đây là sai?
\(a - 5 < a + 2\).
\( - 3a < - 2a\) với \(a < 0\).
\(5a > 10a\) với \(a < 0\).
\(\frac{a}{3} < \frac{a}{2}\) với \(a > 0\).</>
Nếu \[a < b\] thì 2a+1....2b+1.Dấu thích hợp điền vào ô trống là
\[ \ge \].
\[ \le \].
\[ < \].
\[ > \].
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\(2x + 1 > \left( {2x + 4} \right)x\).
\(\frac{{2x}}{3} - 2 < 0\).
>
\(0x - 4 \ge - 4\).
\({x^2} + 2x + 1 \ge 0\).
Giá trị nguyên dương nhỏ nhất của \(x\) thỏa mãn bất phương trình \( - 3x \ge - 9\) là
\(x = 0\).
\(x = 1.\)
\(x = 2\).
\(x = 3\).
Giá trị \[\cos 16^\circ 7'\] gần nhất với số nào sau đây?
\(0,9\).
\(0,96\).
\(0,962\).
\(0,9606\).
Cho tam giác \(ABC\) vuông tại \(A\). Khẳng định nào sau đây là đúng?
\(A{B^2} = B{C^2} + A{C^2}\).
\(\cot B - \tan B = 0\).
\(\sin C = \cos B\).
\(\cot C = \frac{{AC}}{{AB}}\).
Cho tam giác \(ABC\) vuông tại \(A\). Hệ thức nào sau đây là sai?
\(BC = \frac{{AC}}{{\sin B}}\).
\(BC = \frac{{AB}}{{\sin C}}\).
\(BC = \frac{{AC}}{{\cos C}}\).
\(AB = \frac{{AC}}{{\tan C}}\).
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 70^\circ \) và biểu thức: \[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\].
Giá trị của biểu thức \(A\) là
0.
1.
2.
3.
(2,0 điểm)
1. Giải các phương trình sau:
a) \[4x\left( {x + 3} \right) - 3x - 9 = 0.\]
b) \(\frac{{x + 3}}{{x + 1}} - \frac{{x - 1}}{x} = \frac{{{x^2} + 5x + 1}}{{x\left( {x + 1} \right)}}.\)
2. Giải các bất phương trình sau:
a) \[{\left( {x + 2} \right)^2}\; < {x^2} + 5x\;--3.\]
b) \(\frac{{x\left( {x + 1} \right)}}{{12}} - \frac{{x - 1}}{8} \ge \frac{{2{x^2} + 3}}{{24}} + \frac{{5x}}{6}\).
(2,5 điểm)
1. Xác định giá trị của \(a\) và \(b\) để đường thẳng \(y = ax + b\) đi qua hai điểm \(M\left( {3;\,\, - 5} \right)\) và \(N\left( {1;\,\,2} \right).\)
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được số mới lớn hơn số đã cho là \(63\). Tổng của số đã cho và số mới tạo thành bằng \(99\). Tìm số đã cho.
(2,0 điểm)
1. Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\) và \(\widehat {C\,} = 32^\circ .\) Tính độ dài các cạnh còn lại của tam giác \(ABC\) (kết quả làm tròn đến hàng phần trăm).
2. Cho hai tòa nhà 1 và tòa nhà 2 như hình vẽ bên. Trên nóc tòa nhà 2 có một cột ăng-ten thẳng cao \(4\) m. Từ vị trí quan sát \(A\) (trên nóc tòa nhà 1) cao \(7\) m so với mặt đất có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten lần lượt dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang. Tính chiều cao \(CH\) của tòa nhà 2 (làm tròn kết quả đến hàng phần mười).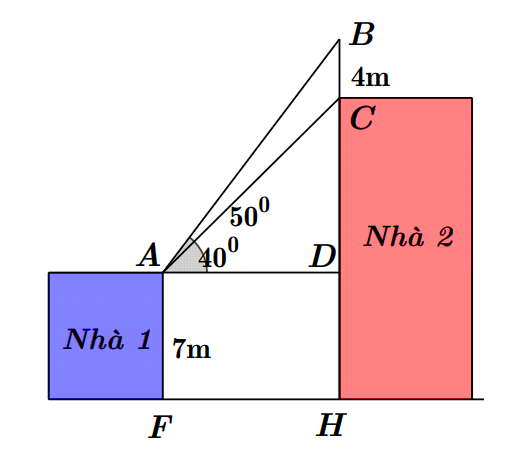
(0,5 điểm) Cho \(a,\,\,b,\,\,c,\,\,d\) là các số thực dương. Chứng minh rằng nếu \(\frac{a}{b} < 1\) thì \(\frac{a}{b} < \frac{{a + c}}{{b + c}}.\,\,\,\left( 1 \right)\)
Áp dụng bất đẳng thức (1) để chứng minh bất đẳng thức sau:
\(1 < \frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < 2\).








