Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án - Đề 7
16 câu hỏi
Bạn An sau khi thực hiện các bước phương trình \(\frac{{2x + 1}}{{x + 1}} + \frac{2}{x} = \frac{2}{{x\left( {x + 1} \right)}}\) nhận được kết quả là \(x = 0\) và \(x = - \frac{3}{2}.\) Khi đó, kết luận bạn An cần viết là
Vậy nghiệm của phương trình đã cho là \(x = 0\).
Vậy nghiệm của phương trình đã cho là \(x = - \frac{3}{2}\).
Vậy nghiệm của phương trình đã cho là \(x = 0;\) \(x = - \frac{3}{2}\).
Vậy phương trình vô nghiệm.
Phương trình \(\left( {x + 4} \right)\left( {8 - x} \right) = 0\) có nghiệm là
\(x = 4;\,\,x = 8\).
\(x = - 4;\,\,x = - 8\).
\(x = 4;\,\,x = - 8\).
\(x = - 4;\,\,x = 8\).
Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có nhiều nhất bao nhiêu nghiệm?
0.
1.
2.
Vô số.
Cho hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\ - 2x + 4y = - 1\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\) và các khẳng định nào sau:
(i) Nhân hai vế của phương trình (1) với 2, rồi cộng từng vế với phương trình (2), ta nhận được phương trình \(0x = 3.\)
(ii) Nhân hai vế của phương trình (1) với 2, rồi cộng từng vế với phương trình (2), ta nhận được phương trình có vô số nghiệm.
(iii) Hệ phương trình đã cho vô nghiệm.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
0.
1.
2.
3.
Phát biểu “\(x\) không lớn hơn \( - 10\)” được viết là
\(x > - 10\).
\[x \ge - 10\].
\(x < - 10\).
</>
\(x \le - 10\).
Cho \(m\) bất kỳ, chọn khẳng định đúng:
\(m - 3 > m - 4\).
\(m - 3 < m - 5\).
</>
\(m - 3 \ge m - 2\).
\(m - 3 \le m - 6\).
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\(x + 2y > 0\).
\(\frac{1}{x} - 3 > 0\).
\({x^2} + 1 > 0\).
\(\frac{x}{2} + 1 > 0\).
Số nguyên nhỏ nhất thỏa mãn bất phương trình \(x\left( {5x + 1} \right) + 4\left( {x + 3} \right) \ge 5{x^2}\) là
\(x = - 3\).
\(x = - 2\).
\(x = - 1\).
\(x = 0\).
Cho tam giác \[MNP\] vuông tại \(M.\) Khi đó \(\cot N\) bằng
\(\frac{{MN}}{{NP}}.\)
\(\frac{{MP}}{{NP}}.\)
\(\frac{{MN}}{{MP}}.\)
\(\frac{{MP}}{{MN}}.\)
Cho góc \(\alpha \) thỏa mãn \(0^\circ < \alpha < 90^\circ \). Biết \(\tan \alpha = \frac{3}{5}\). Giá trị của \(\cot \left( {90^\circ - \alpha } \right)\) bằng
\(\frac{3}{5}\).
\(\frac{4}{5}\).
\(\frac{5}{3}\).
\(\frac{5}{4}\).
Trong tam giác vuông \[ABC\] nếu có \(\widehat {B\,} = 60^\circ \) thì tỉ số giữa cạnh góc vuông \(AC\) và cạnh huyền \(BC\) bằng bao nhiêu?
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{2}\).
\(\frac{{\sqrt 2 }}{2}.\)
1.
Cho \(\Delta ABC\) vuông tại \(A\), có đường cao \(AH\) và \(AB = 13\,\;{\rm{cm}}\), \(BH = 5\;\,{\rm{cm}}{\rm{.}}\) Tỉ số lượng giác \(\sin C\) (làm tròn đến chữ số thập phân thứ hai) bằng
\(\sin C = 2,6\).
\(\sin C \approx 0,385\).
\(\sin C \approx 0,4\).
\(\sin C \approx 0,38\).
(2,0 điểm)
1. Giải các phương trình sau:
a) \[2x\left( {3x - 1} \right) + 6x - 2 = 0\].
b) \(\frac{2}{{x - 3}} - \frac{3}{{x + 3}} = \frac{{3\left( {x + 1} \right)}}{{{x^2} - 9}}\).
2. Giải các bất phương trình sau:
a) \(5 - 7x > 4\left( {x - 3} \right) - 7.\)
b) \(\frac{{x - 1}}{2} - \frac{{7x + 3}}{{15}} \le \frac{{2x + 1}}{3} + \frac{{3 - 2x}}{5}.\)
(2,5 điểm)
1. Xác định \(a\) và \(b\) sao cho hệ phương trình \(\left\{ \begin{array}{l}ax + 2by = - 18\\bx - 3ay = - 3\end{array} \right.\) nhận cặp số \(\left( { - 3;\,\,2} \right)\) làm nghiệm.
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một chiếc thuyền xuôi dòng và ngược dòng trên khúc sông dài \(40\) km hết \(4\) giờ \(30\) phút. Biết thời gian thuyền xuôi dòng \(5\) km bằng thời gian thuyền ngược dòng \(4\) km. Tính vận tốc dòng nước.
(2,0 điểm)
1. Cho tam giác \(ABC\) có đường cao \(AH = 5\,\,{\rm{cm}},\,\,\widehat {B\,} = 70^\circ ,\,\,\widehat {C\,} = 35^\circ .\) Tính độ dài các cạnh của tam giác \(ABC\) (làm tròn kết quả đến chữ số thập phân thứ hai).
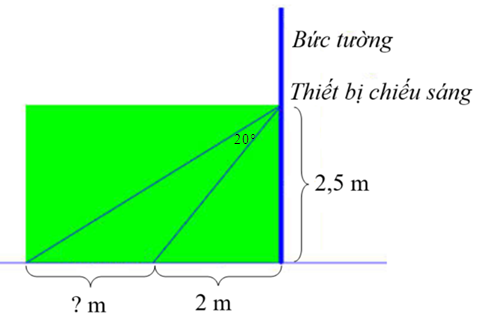
2. Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là \(20^\circ \) và cần đặt cao hơn mặt đất là \(2,5\,\,{\rm{m}}.\) Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường \(2\,\,{\rm{m}}.\) Tính độ dài vùng được chiếu sáng trên mặt đất (làm tròn kết quả đến chữ số thập phân thứ nhất). |
|
(0,5 điểm) Cho hai số thực \[a,\,\,b\] thỏa mãn \[a + b \ne 0.\] Chứng minh bất đẳng thức sau:
\({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} \ge 2.\)