Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 2
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Phương trình nào dưới đây có tập xác định là \(x \ne - 1\) và \(x \ne 3\)?
\(\frac{2}{{x + 1}} = \frac{3}{{x + 3}}.\)
\(\frac{5}{{x - 1}} = \frac{2}{{x - 3}}.\)
\(\frac{{x + 3}}{{x - 1}} = 2.\)
\(\frac{2}{{x + 1}} = \frac{3}{{x - 3}}.\)
Phương trình nào dưới đây là phương trình bậc nhất hai ẩn \(x\) và \(y\)?
\(5x + y = 7.\)
\(2{x^2} + y = 4.\)
\(0x + 0y = - 2.\)
\(2{x^2} + 2{y^2} = 3.\)
Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y = 1\\2x - y = - 1\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2{y^2} = 4\\x + y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2y = 4\\3{x^2} - 2y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} + 2{y^2} = 4\\3x - y = 0\end{array} \right..\)
Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn?
\(x + 2y > 0.\)
\(\frac{1}{x} - 3 > 0.\)
\({x^2} + 1 > 0.\)
\(\frac{x}{2} + 1 > 0.\)
Cho \(a > b\). Khẳng định nào dưới đây là đúng?
\(a - 3 > b - 3.\)
\( - 3a + 4 > - 3b + 4.\)
\(2a + 3 < 2b + 3.\)
\( - 5b - 1 < - 5a - 1.\)
Với mọi số \(a\), ta luôn có:
\(\sqrt {{a^2}} = a.\)
\(\sqrt {{a^2}} = \left| a \right|.\)
\(\sqrt a = \left| a \right|.\)
\(\sqrt {{a^2}} = - a.\)
Điều kiện xác định của căn thức \(\sqrt {2x + 3} \) là
\(x \ge \frac{{ - 3}}{2}.\)
\(x \le \frac{{ - 3}}{2}.\)
\(x \ge \frac{{ - 2}}{3}.\)
\(x \le \frac{{ - 2}}{3}.\)
Điều kiện xác định của căn thức \(\sqrt[3]{{{{\left( {2 - x} \right)}^3}}}\) là
\(x \le 2.\)
\(x \ne 2.\)
\(x < 2.\)
\(\mathbb{R}.\)
Cho tam giác vuông có \(\alpha \) là góc nhọn. Khẳng định nào sau đây là sai?
Tỉ số giữa cạnh huyền và cạnh kề được gọi là cosin của góc \(\alpha \), kí hiệu \(\sin \alpha .\)
Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \alpha .\)
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \), kí hiệu \(\tan \alpha .\)
Tỉ số giữa cạnh kề và cạnh đối được gọi là tang của góc \(\alpha \), kí hiệu \(\cot \alpha .\)
Nếu \(\alpha \) là góc nhọn thì \[\sin \left( {90^\circ - \alpha } \right)\] bằng
\(\sin \alpha .\)
\(\tan \alpha .\)
\(\cos \alpha .\)
\(\cot \alpha .\)
Đường thẳng \(d\) cách tâm \(O\) của đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) một khoảng \({\rm{3 cm}}.\) Khi đó vị trí tương đối của \(d\) và đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) là
Cắt nhau.
Không giao nhau.
Tiếp xúc nhau.
Không kết luận được.
Cho hai đường tròn đồng tâm \(O\) có bán kính lần lượt là \(R\) và \(r{\rm{ }}\left( {R > r} \right).\) Diện tích phần nằm giữa hai đường tròn này – hình vành khăn được tính
\(S = \pi \left( {{r^2} - {R^2}} \right).\)
\(S = \pi \left( {{r^2} + {R^2}} \right).\)
\(S = \pi \left( {{R^2} - {r^2}} \right).\)
Kết quả khác.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Lớp 9A và lớp 9B có tổng cộng \(86\) học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được \(5{\rm{ kg}}\), các bạn còn lại mỗi bạn góp \({\rm{2 kg}}{\rm{.}}\) Biết rằng lớp 9B góp nhiều hơn lớp 9A là \({\rm{8 kg}}\) giấy báo cũ. Gọi \(x\) là số học sinh của lớp 9A, \(y\) là số học sinh của lớp 9B \(\left( {x,{\rm{ }}y \in {\mathbb{N}^ * }} \right)\).
a)\(x + y = 86.\)
b) Phương trình biểu diễn mối liên hệ khối lượng giấy báo cũ giữa hai lớp là \(2x - 2y = 8.\)
c) Hệ phương trình biểu diễn bài toán là \(\left\{ \begin{array}{l}x + y = 86\\y - x = 4\end{array} \right.\).
d) Lớp 9A có \(41\) học sinh, lớp 9B có \(45\) học sinh.
Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Hai người đứng cách nhau \(250{\rm{ m}}\) như hình minh họa dưới đây. (Kết quả làm tròn đến hàng phần trăm)
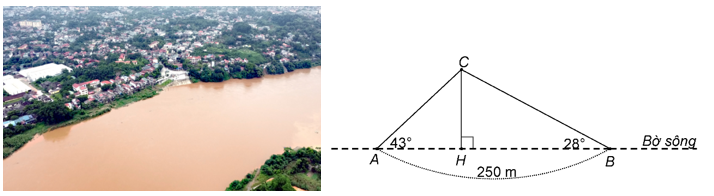
a)\(CH = AH \cdot \tan 43^\circ .\)
b)\(BH = \frac{{CH}}{{\tan 28^\circ }}.\)
c)\(AB = \left( {\tan 43^\circ + \tan 28^\circ } \right)CH\).
d) Cồn cách bờ sông hai người đứng một khoảng lớn hơn \(85{\rm{ m}}{\rm{.}}\)
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{x + 3}}{{x - 2}} - \frac{{x + 1}}{{x + 2}} = \frac{{{x^2} - 4x + 24}}{{{x^2} - 4}}\).
Tìm nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình: \(3x - \left( {6 + 2x} \right) \le 3 \cdot \left( {x + 4} \right)\).
Tính giá trị của biểu thức \(A = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{2\left( {1 - \sqrt x } \right)}}\) với \(x = \frac{1}{{25}}.\)(Kết quả ghi dưới dạng số thập phân)
Một chiếc đèn thả hình vành khuyên, rỗng ở giữa. Biết đường kính của đường tròn lớn là \(90\,{\rm{cm}}\), đường kính của đường tròn nhỏ là \(60\,{\rm{cm}}\). Hỏi diện tích của chiếc đèn bằng bao nhiêu mét vuông? (Kết quả làm tròn đến hàng phần trăm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \(A = \frac{3}{{\sqrt a + 3}}:\left( {\frac{{\sqrt a - 2}}{{\sqrt a + 3}} + \frac{{\sqrt a - 3}}{{2 - \sqrt a }} - \frac{{9 - a}}{{a + \sqrt a - 6}}} \right)\) với \(a \ge 0,{\rm{ }}a \ne 4\) và \(a \ne 9.\)
a) Chứng minh rằng \(A = \frac{3}{{\sqrt x - 2}}\).
b) Tìm \(a\) để \(A + \left| A \right| = 0.\)
(1,5 điểm) Cho \(\Delta ABC\) nhọn có ba đỉnh nằm trên đường tròn \(\left( O \right)\). Điểm \(M\) di động trên cung nhỏ \(BC\). Vẽ \(MH\) vuông góc với \(AB\) ở \(H\), \(MK\) vuông góc với \(AC\) ở \(K\).
a) Chứng minh rằng \(AM\) là đường kính của đường tròn đi qua ba điểm \(A,\,\,H,\,\,K.\)
b) Chứng minh rằng \(HK = AM.\sin \widehat {BAC}\)
c) Xác định vị trí của điểm \(M\) trên cung nhỏ \(BC\) để \(HK\)dài nhất.
(0,5 điểm)Xưa kia có một vị tể tướng nổi tiếng thông thái. Đến khi tể tướng muốn cáo quan về quê, nhà vua liền ban thưởng bằng cách đưa cho tể tướng một đoạn dây dài \[300\] mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Khi đó, mảnh đất hình chữ nhật sẽ thuộc về ngươi”. Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?








