Bộ 5 đề thi Cuối kì 1 Toán 10 Cánh diều cấu trúc mới (có tự luận) có đáp án - Đề 5
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phủ định của mệnh đề “\(\forall x \in \mathbb{R}:{x^2} + 1 > 0\)” là:
“\(\forall x \in \mathbb{R}:{x^2} + 1 = 0\)”.
“\(\exists x \in \mathbb{R}:{x^2} + 1 \le 0\)”.
“\(\exists x \in \mathbb{R}:{x^2} + 1 > 0\)”.
“\(\forall x \in \mathbb{R}:{x^2} + 1 < 0\)”.
Cho \(A = \left\{ {x \in \mathbb{R}|x + 2 \ge 0} \right\}\), \(B = \left\{ {x \in \mathbb{R}|5 - x \ge 0} \right\}\). Khi đó \(A\backslash B\) là
\(\left[ { - 2;5} \right]\).
\(\left[ { - 2;5} \right)\).
\(\left( {5; + \infty } \right)\).
\(\left( {2; + \infty } \right)\).
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - y \ge 3\\x \le y\\x + 3y - 20 < 0\end{array} \right.\).
\(Q\left( {4;\frac{9}{2}} \right)\).
\(M\left( {3;4} \right)\).
\(N\left( {5;5} \right)\).
\(P\left( {5;6} \right)\).
Cho hàm số \(y = f\left( x \right) = 3x - 2\), giá trị của \(f\left( { - 3} \right)\) là
\( - 11\).
\(7\).
\(3\).
\( - 3\).
Đồ thị sau đây là đồ thị của hàm số nào?
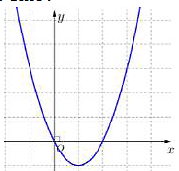
\(y = {x^2} - 2x\).
\(y = - {x^2} + 2x\).
\(y = 2x + 1\).
\(y = 1 - 2x\).
Cho \(90^\circ < \alpha < 180^\circ \). Chọn phát biểu đúng trong các phát biểu sau:
\(\cot \alpha > 0\).
\(\tan \alpha > 0\).
\(\sin \alpha < 0\).
\(\cos \alpha < 0\).
Cho tam giác ABC với AB = c, AC = b, BC = a. Biết c = 14, \(\widehat A = 60^\circ ,\widehat B = 40^\circ \). Làm tròn đến số thập phân thứ nhất thì độ lớn b là
9,14.
9,13.
9,1.
9,2.
Cho 3 điểm phân biệt M, N, P. Hỏi có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \), có điểm đầu và điểm cuối được lấy từ 3 điểm đã cho.
3.
4.
5.
6.
Cho hình thoi ABCD cạnh \(a\) và \(\widehat {BAD} = 60^\circ \). Khi đó \(\left| {\overrightarrow {AD} - \overrightarrow {AB} } \right|\) bằng
\(a\sqrt 2 \).
\(a\).
\(2a\).
\(\frac{{a\sqrt 3 }}{2}\).
Cho ba điểm M, N, P được xác định như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
![]()
\(\overrightarrow {PN} = 4\overrightarrow {MP} \).
\(\overrightarrow {NM} = - 3\overrightarrow {MP} \).
\(\overrightarrow {MN} = 3\overrightarrow {MP} \).
\(\overrightarrow {MN} = - 3\overrightarrow {MP} \).
Cho tam giác đều \(ABC\) cạnh \(a\). Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
\(0,5{a^2}\).
\({a^2}\).
\(2{a^2}\).
\(3{a^2}\).
Tập nghiệm của bất phương trình \({x^2} - 9 \le 0\) là
\(\left( { - 3;3} \right)\).
\(\left[ { - 3;3} \right]\).
\(\left( { - \infty ;3} \right) \cup \left( {3; + \infty } \right)\).
\(\left[ { - 9;9} \right]\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho \(\Delta ABC\) vuông tại A, có \(AB = a\). Gọi E và F lần lượt là trung điểm của AC và AB.
a)\(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {EF} \).
b)\({S_{\Delta BEF}} = \frac{{{a^2}}}{8}\).
c)\(\left| {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AC} } \right| = \frac{{a\sqrt 5 }}{2}\).
d) \(\cos \left( {\overrightarrow {BE} ,\overrightarrow {CF} } \right) = - \frac{1}{{\sqrt 5 }}\).
Cho đồ thị hàm số bậc hai \(y = f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) như hình vẽ
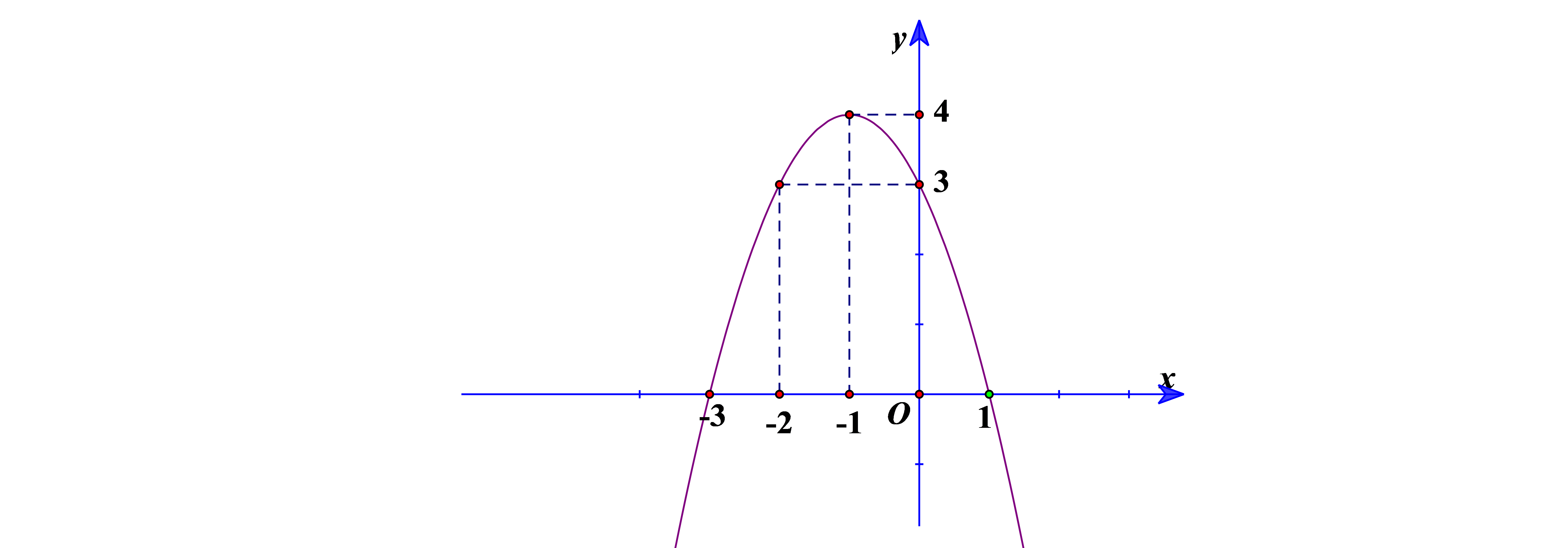
a) Hàm số đã cho có \(a > 0\).
b) Đồ thị hàm số đã cho có tọa độ đỉnh \(I\left( { - 1;4} \right)\).
c) Với \(x \in \left( { - 3;1} \right)\) thì \(f\left( x \right) > 0\).
d) Các hệ số \(a,b,c\) của hàm số đã cho thỏa mãn đẳng thức \(a + b + c = 0\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho các tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 3 \le x \le 5} \right\};B = \left\{ {x \in \mathbb{R}|x \le 2} \right\}\). Tập \(A\backslash B\) có bao nhiêu số nguyên?
Gia đình anh Hùng dự định trồng rau và hoa trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha rau thì cần 20 ngày công và thu lợi 3 triệu đồng. Nếu trồng 1 ha hoa thì cần 30 ngày công và thu lợi 4 triệu đồng. Biết rằng, gia đình anh Hùng chỉ có thể sử dụng không quá 180 ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, anh Hùng có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng?
Cho phương trình \(\sqrt {{x^2} + 2x + 4} = \sqrt {2 - x} \). Phương trình có bao nhiêu nghiệm nguyên?
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên (tham khảo hình vẽ).
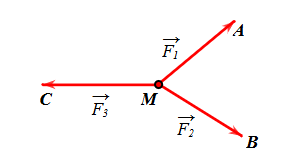
Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng \(100\sqrt 2 \)N và góc \(\widehat {AMB} = 90^\circ \). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (đơn vị N).
PHẦN II. TỰ LUẬN
Trong bốn điểm \(M\left( {2; - 4} \right),N\left( { - 1;3} \right),P\left( {1;3} \right),Q\left( { - 2; - 3} \right)\). Điểm nào thuộc miền nghiệm của bất phương trình \(5x - 2y \ge 2\).
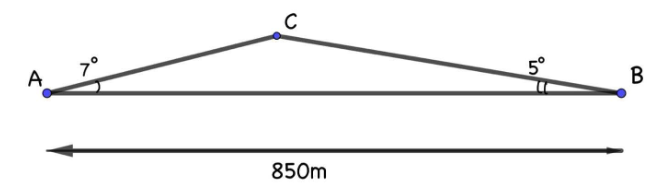
Bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (như hình vẽ) với C là đỉnh dốc. Cho biết đoạn thẳng AB dài 850 m, \(\widehat A = 7^\circ ,\widehat B = 5^\circ \), vận tốc trung bình khi lên dốc là 4 km/h và khi xuống dốc là 19 km/h. Hỏi bạn An đi từ nhà đến trường hết bao nhiêu phút (làm tròn kết quả cuối cùng đến hàng đơn vị không làm tròn các kết quả trung gian).
Một doanh nghiệp tư nhân chuyên kinh doanh tủ lạnh các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh tủ lạnh Hitachi với chi phí mua vào một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng tủ lạnh mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng tủ lạnh đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc tủ lạnh thì số lượng tủ lạnh bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.








