12 câu hỏi
Cho các biểu thức: \[{x^2} + {y^2};\] \[2\,\,025;\] \[\frac{3}{x} + y;\] \[\frac{x}{y} + \frac{1}{5}x;\] \[\frac{x}{2} + xyz;\] \[4 + x\sqrt {yz} \] có bao nhiêu đa thức?
1.
2.
3.
4.
Đơn thức \[6{x^4}{y^3}\] chia hết cho đơn thức nào sau đây?
\[6{x^4}{y^3}z\].
danh từ: nốt si
\[4{x^5}y\].
\[2{x^3}\].
\[3{x^4}{y^4}\].
Khẳng định nào sau đây đúng?
\({\left( { - x - 3} \right)^2} = {\left( {x + 3} \right)^2}.\)
\({\left( {x - 2} \right)^2} = {x^2} - 4.\)
\({\left( {y - 2} \right)^3} = {\left( {2 - y} \right)^3}.\)
\({\left( {x - 3} \right)^2} = - {\left( {3 - x} \right)^2}.\)
Cho hai phân thức có mẫu thức là \(2{x^3}{y^2}\left( {y - 1} \right)\) và \({x^2}{y^3}{\left( {y - 1} \right)^2}.\) Mẫu thức chung của hai phân thức đó là
\(2{x^3}{y^3}\left( {y - 1} \right).\)
\(2{x^3}{y^3}{\left( {y - 1} \right)^2}.\)
\({x^3}{y^3}{\left( {y - 1} \right)^2}.\)
\(2{x^2}{y^3}{\left( {y - 1} \right)^2}.\)
Cho hàm số \(y = f\left( x \right) = 2{x^2} - 1.\) Khẳng định nào sau đây là đúng?
\(f\left( { - 1} \right) = - 3.\)
\(f\left( 1 \right) = 1.\)
\(f\left( { - 1} \right) = - 1.\)
\(f\left( 1 \right) = 3.\)
Giá trị của \(m\) để đồ thị hàm số \(y = \left( {m + 2} \right)x + 5\) là đường thẳng có hệ số góc bằng \( - 3\) là
\(m = 5.\)
\(m = 3.\)
\(m = - 3.\)
\(m = - 5.\)
Nhận định nào sau đây là đúng?
Nếu hình chóp có đáy là hình thoi, chân đường cao trùng với tâm hình thoi thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình chữ nhật, chân đường cao trùng với giao điểm của hai đường chéo đáy thì nó là hình chóp đều.
Nếu hình chóp có đáy là hình vuông thì nó là hình chóp đều.
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Một hình chóp đều và một hình lăng trụ đứng có diện tích đáy bằng nhau. Chiều cao của hình chóp đều gấp đôi chiều cao của hình lăng trụ đứng. Thể tích của hình chóp đều là
\(V = \frac{1}{3}Sh.\)
\[V = Sh.\]
\(V = \frac{2}{3}Sh.\)
\(V = 2Sh.\)
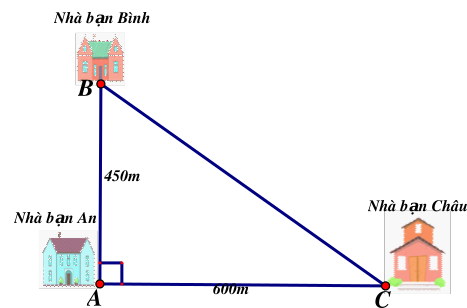
Nhà bạn An (vị trí \[A\] trên hình vẽ) cách nhà bạn Châu (vị trí \[C\] trên hình vẽ) \[600\,\,{\rm{m}}\]và cách nhà bạn Bình (vị trí \[B\] trên hình vẽ) \[450\,\,{\rm{m}}.\] Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là ba đỉnh của một tam giác vuông (như hình vẽ). Tính khoảng cách từ nhà Bình đến nhà Châu.
\[396{\rm{ m}}\].
\[750{\rm{ m}}\].
\[150{\rm{ m}}\].
\[250{\rm{ m}}\].
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(D,\,\,E\) theo thứ tự thuộc các cạnh bên \(AB,\,\,AC\) sao cho \(DE\,{\rm{//}}\,BC\). Tứ giác \(BDEC\) là hình gì?
Hình thang cân.
Hình thang vuông.
Hình bình hành.
Hình thoi.
Phân tích đa thức \({x^5} - {x^3} - {x^2} + 1\) thành nhân tử ta được
\[{\left( {x + 1} \right)^2}\left( {x - 1} \right)\left( {{x^2} + x + 1} \right).\]
\[{\left( {x + 1} \right)^2}\left( {x - 1} \right)\left( {{x^2} - x + 1} \right).\]
\[{\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + x + 1} \right).\]
\[{\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} - x + 1} \right).\]
Với điều kiện các phân thức có nghĩa. Phân thức \(\frac{{ - 2xy}}{{6{x^3}{y^2}}}\) bằng phân thức nào sau đây?
\(\frac{{ - 1}}{{3x{y^2}}}.\)
\(\frac{{ - 1}}{{3{x^2}y}}.\)
\(\frac{{ - 0}}{{{x^2}y}}.\)
\(\frac{{ - 1}}{{2{x^2}y}}.\)
