12 câu hỏi
Đa thức nào sau đây chưa thu gọn?
\[4{x^2} + x - y\].
\[{x^4}y + x - 2y{x^4}\].
\[ - {x^3}y + \frac{2}{5}{y^2}\].
\[\frac{{x + 2y}}{5}\].
Bậc của biểu thức \(A = 2{x^2}y \cdot 5x{y^3}\) là
\(5\).
\(6\).
\(7\).
\(8\).
Cho các đơn thức \(A = 4{x^3}y\left( { - 5xy} \right)\), \(B = {x^4}{y^2}\), \(C = - 5{x^2}{y^4}\). Các đơn thức nào sau đây đồng dạng với nhau?
Đơn thức \(A\) và đơn thức \(C\).
Đơn thức \(B\) và đơn thức \(C\).
Đơn thức \(A\) và đơn thức \(B\).
Cả ba đơn thức \(A,B,C\) đồng dạng với nhau.
Cho biểu thức \(H = \left( {2x - 3} \right)\left( {x + 7} \right) - 2x\left( {x + 5} \right) - x\). Khẳng định nào sau đây là đúng?
\(H = 21 - x\).
\(H > 0\).
\(H < - 1\).
\(10 < H < 20\).
Đẳng thức nào sau đây là hằng đẳng thức?
\({x^2} - x = - x + {x^2}\).
\(x\left( {x - 1} \right) = x - {x^2}\).
\({\left( {a - b} \right)^2} = - {\left( {b - a} \right)^2}\).
\(a - 2 = 2 - a\).
Kết quả phân tích đa thức \(6{x^2}y - 12x{y^2}\) là
\(6xy\left( {x + y} \right)\).
\(6xy\left( {x - y} \right)\).
\(6xy\left( {x + 2y} \right)\).
\(6xy\left( {x - 2y} \right)\).
Phân thức \(\frac{A}{B} = \frac{C}{D}\,\,\left( {A,\,\,B \ne 0} \right)\) khi
\(AB = CD\).
\(AD = BC\).
\(\frac{A}{D} = \frac{C}{B}\).
\(\frac{A}{D} = \frac{B}{C}\).
Phân thức \(\frac{{1 - x}}{{y - x}}\) bằng với phân thức nào sau đây?
\(\frac{{x - 1}}{{y - x}}\).
\(\frac{{1 - x}}{{x - y}}\).
\(\frac{{x - 1}}{{x - y}}\).
\(\frac{{y - x}}{{1 - x}}\).
Khẳng định nào sau đây là đúng?
Hình chóp tam giác đều có 3 mặt.
Hình chóp tứ giác đều có 4 đỉnh.
Hình chóp tứ giác đều có đáy là hình thoi.
Hình chóp tam giác đều có 6 cạnh.
Một hình chóp tứ giác đều có cạnh đáy là \(a\) và độ dài trung đoạn là \(b\) thì có diện tích xung quanh là
\({S_{xq}} = 2ab.\)
\({S_{xq}} = ab.\)
\({S_{xq}} = \frac{1}{2}ab.\)
\({S_{xq}} = 4ab.\)
Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AH.\)Biết \(AH = 4\;\;{\rm{cm}},\,\,AB = 5\;\;{\rm{cm}}.\) Chu vi tam giác \(ABC\) bằng
\(16\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
\(12\;\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
Đường chéo của tứ giác lồi \(ABCD\)là
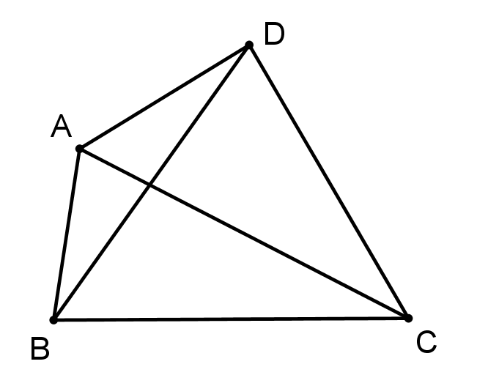
\[AB,\,\,CD\].
\[BC,\,\,CD\].
\(AC,\,\,BD\).
\(AC,\,\,CD\).
Gợi ý cho bạn
Xem tất cảBộ 10 đề thi học kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 5