12 câu hỏi
Trong các biểu thức đại số sau, biểu thức nào là đơn thức?
\(\frac{{2x}}{y}\).
\(3x + 2y\).
\(4\left( {x - y} \right)\).
\( - \frac{2}{3}x{y^2}\).
Kết quả của phép chia \(5{x^2}{y^5}:10{x^2}{y^3}\) là
\({y^4}\).
\(\frac{1}{2}x{y^3}\).
\(50{x^4}{y^8}\).
\(\frac{1}{2}{y^2}\).
Cặp đơn thức nào sau đây không đồng dạng?
\(7{x^3}y\) và \(\frac{1}{{15}}{x^3}y\).
\( - \frac{1}{8}{\left( {xy} \right)^2}{x^2}\) và \(32{x^2}{y^3}\).
\(5{x^2}{y^2}\) và \( - 2{x^2}{y^2}\).
\(a{x^2}y\) và \(2b{x^2}y\)\((a,b\) là các hằng số khác \(0).\)
Thu gọn đa thức \(Q = {x^2} + {y^2} + {z^2} + {x^2} - {y^2} + {z^2} + {x^2} + {y^2} - {z^2}\) được kết quả là
\(Q = 3{x^2} + 3{y^2} + 3{z^2}\).
\(Q = {x^2} + {y^2} + {z^2}\).
\(Q = 3{x^2} + {y^2} + {z^2}\).
\(Q = 3{x^2} - {y^2} - {z^2}\).
Khẳng định nào sau đây là sai?
\({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\).
\({\left( {x + y} \right)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\).
\({x^3} - {y^3} = \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\).
\({\left( {x - y} \right)^3} = {x^3} - {y^3}\).
Cho \({x^3} + 12{x^2} + 48x + 64 = {\left( {x + a} \right)^3}\). Giá trị của \(a\) là
4.
64.
\( - 4\).
\( - 64\).
Phân thức nào sau đây bằng với phân thức \(\frac{y}{{3x}}\) (với giả thiết các phân thức đều có nghĩa)?
\(\frac{{3{y^2}}}{{9x{y^2}}}\).
\(\frac{{{y^2}}}{{9x{y^2}}}\).
\(\frac{{3{y^2}}}{{9xy}}\).
\(\frac{{3y}}{{9x{y^2}}}\).
Quy đồng mẫu thức hai phân thức \(\frac{2}{{{x^2}y}}\) và \(\frac{3}{{x{y^2}}}\) ta được mẫu thức chung là
\({x^2}y\).
\(x{y^2}\).
\({x^2}{y^2}\).
\({x^3}{y^3}\).
Cho các hình dưới đây.

Hình có dạng là hình chóp tam giác đều là
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Một hình chóp tứ giác đều có diện tích xung quanh \({S_{xq}}\) và chiều cao \(h\). Khi đó nửa chu vi đáy là
\(\frac{{2{S_{xq}}}}{h}\).
\(\frac{{{S_{xq}}}}{h}\).
\(\frac{{{S_{xq}}}}{{2h}}\).
\(\frac{{2h}}{{{S_{xq}}}}\).
Cho tam giác \[ABC\]có độ dài ba cạnh \[AB = 6{\rm{ cm}},{\rm{ }}BC = 8{\rm{ cm}},{\rm{ }}AC = 10{\rm{ cm}}.\]Khẳng định nào sau đây là đúng?
Tam giác \[ABC\] vuông tại\[A\].
Tam giác \[ABC\] vuông tại\[B\].
Tam giác \[ABC\] vuông tại\[C\].
Tam giác \[ABC\] đều.
Cho hình vẽ bên. Khẳng định nào sau đây là sai?
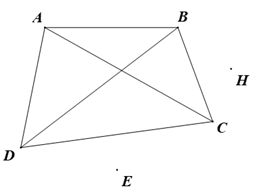
Hai cạnh \(AB\)và \[BC\] kề nhau.
Hai cạnh \[BC\] và \[DA\] đối nhau.
Các cặp góc \[\widehat A\] và \[\widehat B\,;\,\,\widehat C\] và \[\widehat D\]đối nhau.
Các điểm \[H\] và \[E\]nằm ngoài.
